

| © CAMBRIDGE UNIVERSITY PRESS 1999 |
5. Seeds of Grand Creation
The clustering of galaxies became a challenge that
devoured Lemaître's research in cosmology. Time and
again Shapley demanded that the theory of the
expanding universe account for concentrations of
nebulae he was charting close to the Milky Way.
Lemaître wanted foremost to satisfy the demand. Yet
to the end of his life the solution eluded him.
Deprit (1983)
Two of the three main ingredients for understanding the universe during the first half of the twentieth century were observational: its immense size and its expansion. The third was Einstein's general theory of relativity. It related the force of gravity to the structure of spacetime. Two years after his definitive account of the theory, Einstein (1917) applied it to cosmology. His first model, introducing the cosmological constant, was static - matter without motion. Shortly afterward deSitter (19 17a,b) discovered an expanding but empty solution of Einstein's equations - motion without matter. Then Friedmann (1922) found the intermediate solutions with both expansion and matter, which Lemaître (1927) independently rediscovered. Eddington (1930, 193 Ia) was about to publish them independently yet again when Lemaître, who had formerly been his student, gently reminded him that they were already known. So Eddington publicized these solutions more widely and also showed that Einstein's static universe would become unstable if condensations formed within it.
A small fraction of cosmological thought during this period
strayed from the homogeneous models to the nature and origin of
structure in the universe. Charlier (1908, 1922; see also Smart, 1922)
suggested a relation between the structure and the size of the
universe. If the universe is infinite and has an average uniform density
 0,
then by Newton's law the total radial gravitational force
on a typical particle of mass m is
0,
then by Newton's law the total radial gravitational force
on a typical particle of mass m is
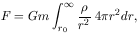 |
(5.1) |
which is infinite. (The net vectorially averaged force, however, would be zero for strict uniformity.) Newton himself recognized this problem (see Chapter 2) and it was emphasized by Seeliger (1895). If we substitute luminosity, which also decreases as the inverse square of the distance, for gravity, we obtain the well-known Olbers' paradox (Harrison 1965, 1987; Landsberg, 1972). Luminous sources of finite extent saturate the solid angle if we can see to large enough distances. They then absorb as much as they emit, giving a uniform finite sky brightness, provided there has been enough time to reach equilibrium. Day and night are equally bright. The actual departure from equilibrium resolves Olbers' paradox. But in Newton's theory, gravity is not absorbed and it propagates infinitely rapidly; so it leads to an infinite total force in this model.
Charlier's attempt to resolve this difficulty was a hierarchical distribution of the matter. He anticipated the modern fractal description of clustering (see Chapter 12). Suppose in the simplest version of this model that the lowest level, L0, of the hierarchy contains single objects of mass M0. The next level, L1, has spherical clusters each with N1 of the basic objects. In turn, N2 of these clusters are themselves spherically clustered to form the L2 level and so on. The total mass at the L2 level is M2 = N2 M1 = N2 N1 M0, and generally Mi = Ni Mi - 1. If the radius of each level is Ri, and we consider the gravitational force on a single basic object at the surface of an L1 cluster, which in turn is at the surface of an L2 cluster, which in turn ... we obtain
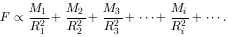 |
(5.2) |
This series converges if
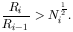 |
(5.3) |
Notice that for the density,
 i, =
Mi / Ri3, the above
inequality implies
i, =
Mi / Ri3, the above
inequality implies
 i
< Ni-1/2
i
< Ni-1/2
 i - 1,
so that the average density decreases at each
level of the hierarchy. Therefore
i - 1,
so that the average density decreases at each
level of the hierarchy. Therefore
 i
i
 0 on very
large scales in this
model, even though there is a finite gravitational force caused by the
correlations of matter on smaller scales. Using the observed numerical
values of his day Charlier concluded that his inequality (5.3) was
satisfied up to at least L2 (as it is with modern
values) and this was a satisfactory description of our universe. Kant's
view of the Universe was now quantified.
0 on very
large scales in this
model, even though there is a finite gravitational force caused by the
correlations of matter on smaller scales. Using the observed numerical
values of his day Charlier concluded that his inequality (5.3) was
satisfied up to at least L2 (as it is with modern
values) and this was a satisfactory description of our universe. Kant's
view of the Universe was now quantified.
The unsatisfactory features of this approach are its artificiality and lack of any dynamical explanation and (we now know) its instability. If such an arrangement of matter were imposed by fiat upon the Universe, the mutual gravitational forces among clusters would destroy it. A truly stationary self-consistent solution, or an origin for evolving structure, needed to be found.
Jeans proposed an origin; in fact he proposed two. Like Hubble
and Shapley (and later Hoyle and Ryle), Jeans and Eddington were
personal antagonists whose rivalry stimulated astronomy. Whereas
Eddington asked what a perturbation can do for the Universe, Jeans
asked what the Universe can do for a perturbation. A static universe,
Jeans (1902a.b) found, causes gravitationally unstable linear density
perturbations to grow exponentially fast with a timescale
1 / (G
 )1/2.
His criterion for instability, which we will see more of in Chapter 16. is
essentially that the region be large enough that its gravitational
potential energy,
~ G M2 / R, exceeds its kinetic energy,
M v2 / 2, or approximately
)1/2.
His criterion for instability, which we will see more of in Chapter 16. is
essentially that the region be large enough that its gravitational
potential energy,
~ G M2 / R, exceeds its kinetic energy,
M v2 / 2, or approximately
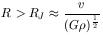 |
(5.4) |
in terms of the average density
 and velocity
dispersion v2
and velocity
dispersion v2
 kT /
mp,
where k is Boltzmann's constant, T is the temperature, and
mp
is the mass of an individual particle. Since (G
kT /
mp,
where k is Boltzmann's constant, T is the temperature, and
mp
is the mass of an individual particle. Since (G
 )-1/2
is the
characteristic gravitational response time of a region,
RJ is roughly
the distance an average particle can travel during this time.
)-1/2
is the
characteristic gravitational response time of a region,
RJ is roughly
the distance an average particle can travel during this time.
This seemed to solve the problem of the origin of galaxies and nearly three decades later Jeans (1929) wrote:
We have found that, as Newton first conjectured, a chaotic mass of gas of approximately uniform density and very great extent would be dynamically unstable; nuclei would tend to form in it, around which the whole of the matter would ultimately condense. We have obtained a formula which enables us to calculate the average distance apart at which these nuclei would form in a medium of given density, and this determines the average mass which would ultimately condense round each.
If all the matter of those parts of the universe which are accessible to our observation, a sphere of about 140 million light years radius [here Jeans used Hubble's estimate of the useful range of the 100-inch Mount Wilson telescope], were spread out uniformly, it would form of gas of density 10-31 [g cm-3 or thereabouts. We have calculated that the gravitational instability would cause such a medium to break up into detached bodies whose distance apart would be of the same order as the observed distance between spiral nebulae; the mass of each such body would accordingly be about equal to the mass of the average spiral nebula. We may conjecture, although it is improbable that we shall ever be able to prove, that the spiral nebulae were formed in this way. Any currents in the primeval chaotic medium would persist as rotations of the nebulae, and as these would be rotating with different speeds. they might be expected to shew all the various types of configurations .. actually observed.
Jeans's description is reminiscent of the myths of the Marquesas Islands, mentioned in Chapter 1.
Unfortunately Jeans's description also contains an element of
myth because he did not properly take the expansion of the Universe
into account. Remarkably, it would be nearly half a century after
Jeans's original work, and two decades after the Universe was known to
expand, before self-consistent solutions of gravitational instability
in an expanding universe were calculated: first by Lifshitz (1946) for
the relativistic case and then by Bonnor (1957) for the simpler
Newtonian approximation. Equation (5.4) still gives the basic
instability criterion, but in the expanding universe the instability
grows much more slowly. A small relative density enhancement,

 /
/
 ,
typically grows algebraically in proportion to the radius of the
universe, rather than exponentially with a timescale 1 / (G
,
typically grows algebraically in proportion to the radius of the
universe, rather than exponentially with a timescale 1 / (G
 )1/2
as in the static case. This is because the universe expands on about the
same 1 / (G
)1/2
as in the static case. This is because the universe expands on about the
same 1 / (G
 )1/2
timescale that the instability tries to grow. The
decreasing density almost quenches the instability, leaving only a
residual slow algebraic growth of perturbations. Consequently galaxies
do not have enough time to form from simple N1/2
fluctuations (especially when the effects of the cosmic black body radiation
background discovered in 1965 are considered - see Partridge,
1995). The galaxy formation problem remains essentially unsolved.
)1/2
timescale that the instability tries to grow. The
decreasing density almost quenches the instability, leaving only a
residual slow algebraic growth of perturbations. Consequently galaxies
do not have enough time to form from simple N1/2
fluctuations (especially when the effects of the cosmic black body radiation
background discovered in 1965 are considered - see Partridge,
1995). The galaxy formation problem remains essentially unsolved.
Jeans (1929) hedged his bet, however, in a very imaginative way. Difficulties in understanding the spiral structure of galaxies in the 1 920s led him to propose that:
Each failure to explain the spiral arms makes it more and more difficult to resist a suspicion that the spiral nebulae are the seat of types of forces entirely unknown to us, forces which may possibly express novel and unsuspected metric properties of space. The type of conjecture which presents itself, somewhat insistently, is that the centers of the nebulae are of the nature of "singular points," at which matter is poured into our universe from some other, and entirely extraneous spatial dimension, so that, to a denizen of our universe, they appear as points at which matter is being continually created.
Although we now have a good understanding of the galactic instabilities that produce spiral arms, new evidence of violent activity from quasars and active galactic nuclei has convinced a small minority of astronomers (see Arp, 1987) that Jeans might have been right. If so, it provides a completely different view of the origin of galaxies. Instead of condensing, they would be ejected from singularities in the structure of space-time.
A variety of other ideas, mainly explored by Eddington, Lemaître, and Milne, competed with gravitational instability to explain galaxy formation and clustering in the 1930s. In fact Eddington (193 ib) did not approve of gravity as an explanation of clustering, and in his Presidential address to the Mathematical Association remarked: "It is probable that the spiral nebulae are so distant that they are very little affected by mutual gravitation and exhibit the inflation effect in its pure form. It has been known for some years that they are scattering apart rather rapidly, and we accept their measured rate of recession as a determination of the rate of expansion of the world." Although Eddington was properly more cautious than Jeans and more aware of the effects of expansion, he (like Gamow and Teller, 1939) missed two major points which accentuate the gravitational clustering of galaxies. First, when the galaxies are closer together at earlier times, the graininess of the gravitational field causes galaxy positions to become correlated during just one or two expansion timescales (this was not fully realized until four decades later). These correlations resulting from the interactions of nearest neighbor galaxies lead to the formation of small groups. Second, as the universe continues to expand each group begins to act approximately like a single particle with its large total mass. The groups themselves become correlated over larger scales and more massive clusters build up. The clustering is rescaled to larger and larger distances whose limit is determined by the time available for structure to form. Thus a hierarchical distribution can build up, although it differs significantly in detail from the form Charlier suggested.
In the same Presidential address, Eddington's comments on entropy stimulated Lemaître's concept of the Primeval Atom. Eddington had described the need for increasing entropy and disorganization in order to provide a measure of time. Lemaître (1931) connected disorganization with fragmentation and pursued this notion back to the origin of the Universe:
... the present state of quantum theory suggests a beginning of the world very different from the present order of Nature. Thermodynamical principles from the point of view of quantum theory may be stated as follows: (I) Energy of constant total amount is distributed in discrete quanta. (2) The number of distinct quanta is ever increasing. If we go back in the course of time we must find fewer and fewer quanta, until we find all the energy of the universe packed in a few or even a unique quantum.
Now, in atomic processes, the notions of space and time are no more than statistical notions; they fade out when applied to individual phenomena involving but a small number of quanta. If the world has begun with a single quantum, the notions of space and time would altogether fail to have any meaning at the beginning; they would only begin to have a sensible meaning when the original quantum had been divided into a sufficient number of quanta. If this suggestion is correct, the beginning of the world happened a little before the beginning of space and time.
The critical difference with gravitational instability was that in Lemaître's (1950, p. 77) cosmology:
The world has proceeded from the condense to the diffuse. The increase of entropy which characterizes the direction of evolution is the progressive fragmentation of the energy which existed at the origin in a single unit. The atom-world was broken into fragments, each fragment into still smaller pieces. To simplify the matter, supposing that this fragmentation occurred in equal pieces, two hundred and sixty generations would have been needed to reach the present pulverization of matter into our poor little atoms, almost too small to be broken again.
The evolution of the world can be compared to a display of fireworks that has just ended: some few red wisps, ashes and smoke. Standing on a well-chilled cinder, we see the slow fading of the suns, and we try to recall the vanished brilliance of the origin of the worlds.
As fossil evidence for these primordial fireworks, Lemaître often cited the cosmic rays, but we now believe these high-energy particles and photons have a much later origin in supernovae, pulsars, active stars, galactic nuclei, and quasars.
Lemaître's grand picture of creation was firmly attached to his mathematical model of a universe with nonzero cosmological constant. This term in the Einstein-Friedmann equations essentially acts as a repulsive force whose strength increases with distance. It leads to three stages in the expansion of the Universe. First, there is a period of rapid expansion, which Lemaître identified with the break up of the primeval universe-atom. Second, there ensues a period of very slow expansion when the cosmological repulsion is just slightly greater than the overall gravitational attraction. Third, there is a final stage in which we now exist when the cosmological repulsion becomes much greater than gravity and the Universe again expands very rapidly.
Successive fragmentations during the first stage result in particles whose velocities are not exactly equal to the average expansion. These peculiar velocities enhance any density fluctuations that may be present and produce clouds. Then when the expansion slows (Lemaître, 1961):
One of the effects of the fluctuations of density from place to place is to divide space into attractive regions and repellent regions. The attractive regions will exert a selection effect on the gaseous clouds that fill space and have a distribution of velocities up to a high limit. The clouds that have a velocity not too different from that of an attractive region will remain in or near it and form an assembly from which a galaxy later evolves. The important point is that these protogalaxies do not arise, as in other theories, from some effect due to numerous collisions, but only from a selection effect. Collisions would, of course, reduce the velocities, while a selection produces protogalaxies with the same velocities as the attractive regions. These velocities arise from fluctuations of density in the swarm of the swiftly moving clouds and may therefore be expected to be fairly large.
Repetition of this same process with individual galaxies instead of clouds would produce the clusters of galaxies. Therefore an individual cluster's growth cannot be considered in isolation from its neighboring clusters, and galaxies would be exchanged between clusters and the field.
Gravitational dynamics play a major role in this clustering. Overdense regions gravitationally attract galaxies from the field and can bind them if their initial total energy relative to the region is (by selection) low. As a cluster forms, it can also expel members by many-body interactions, leaving the remaining cluster more tightly bound. Galaxies with relatively high velocities will go right through the cluster unless they happen to be captured gravitationally by a rare close encounter.
Although Lemaître began to consider a mathematical
formulation, and even started a numerical simulation of clustering, he
did not make much progress. Interest in Lemaître-type universes
diminished as it became the fashion to set the cosmo- logical constant
to zero, although there was a brief revival in the late 1 960s when it
appeared, temporarily, that quasar redshifts strongly clustered around
z  1.95. This
could be identified with the stagnation era in the
Lemaître model, and it led to a detailed linear perturbation analysis
(Brecher and Silk, 1969) of the growth of galaxies and its relation to
the stability of the model. This quasar clustering turned out,
however, to be an artefact of observational selection. Some
inflationary models of the very early Universe require a nonzero value
of
1.95. This
could be identified with the stagnation era in the
Lemaître model, and it led to a detailed linear perturbation analysis
(Brecher and Silk, 1969) of the growth of galaxies and its relation to
the stability of the model. This quasar clustering turned out,
however, to be an artefact of observational selection. Some
inflationary models of the very early Universe require a nonzero value
of  . Recent
observations of the recession velocities of high redshift
galaxies, whose actual distances are found from a type of supernova
which may be a good standard candle, suggest a nonzero
. Recent
observations of the recession velocities of high redshift
galaxies, whose actual distances are found from a type of supernova
which may be a good standard candle, suggest a nonzero
 . Its value
is still very uncertain.
. Its value
is still very uncertain.
Quite different reasons had led Milne (1935) to a nongravitational view of galaxy formation and clustering. He developed an alternative cosmology based on "kinematic relativity." His universe was flat and expanded everywhere and always at the speed of light from an initial singularity. Its smoothed out identical appearance to any observer moving with this expansion (which Milne called the Cosmological Principle) meant that such a fundamental observer would see the faster moving objects proportionally farther away. A linear redshift-distance relation thus arose solely from the kinematics of the expansion (as it would in any statistically homogeneous model). Small variations in the velocities of particles that emerged from the "preexperimental singularity" would produce regions where the faster moving particles would catch up with more distant slower moving ones and produce clumps. "No `process of condensation' has `caused' the nuclear agglomerations; the word `condensation' suggests inward motions, but the relative motions have been invariably outward." Definite predictions followed for the spatial density distribution in the congested regions. They do not agree with more recent observations. Although Mime elaborated his theory with great ingenuity from simple premises, it declined rapidly in interest as the dominant role of local gravity became more clearly and widely recognized.
In its most extreme form, local gravity could cause the capture of galaxies by tidal dissipation of their orbital energy. Holmberg (1940) showed this might produce the observed clustering if the Universe were static, but not if it expands. So good was the agreement of his theory with the observed probability of finding binary and small multiple systems that he thought it strong evidence that the Universe really was static. It was a case of too many free parameters chasing too few observations. Nonetheless, several important results came out of Holmberg's analysis: He made the first reasonable estimate of the observed multiplicity function - the relative number of groups having N galaxies. He also plotted the probability for finding N galaxies in a given size area of the sky centered on a galaxy. Holmberg's technique differed from Hubble's counts, which were centred at arbitrary positions. The results of these galaxy-centered cells also had a non-Poisson distribution. This differed from Hubble's counts centered at arbitrary positions and also from a Poisson distribution. It was a forerunner of the correlation and fractal statistics. He made one of the first quantitative comparisons between galaxy type and the presence of companions. This was to search for evidence of tidal interaction, and it revealed the influence of environment on galaxies. To determine the tidal effects of close galaxy interactions, Holmberg (1941) constructed an "analog computer" in which light substituted for gravity. The mass elements of each interacting galaxy were represented by thirty-seven light bulbs, specially constructed to radiate in a plane with constant, equal, isotropic luminosities. Their inverse square law illumination at any position was detected by a photocell to provide the net effective gravitational force. The bulb at this position was then moved in response to this force, and the process repeated to mimic the system's gravitational evolution. Crude but pioneering results showed that the orbits lost enough energy for the galaxies to merge and, in merging, to produce streams of stars and spiral arms.
With hindsight it is easy to see where each of these theories was incomplete or went astray. Their great achievement was to begin to quantify ideas going back to the ancient Greeks and struggling to emerge through a cloudy filter of observations. The next stage, after the greatly reduced astronomical activity of the 1940s, was to sharpen the statistical tools for analyzing galaxy positions.