© CAMBRIDGE UNIVERSITY PRESS 1999

6. Clusters versus Correlations

How should the irregular distribution of galaxies be described statistically? Are clusters the basic unit of structure among the galaxies, or is this unit an individual galaxy itself? Two new themes and the start of a theory emerged during the 1 950s and early 1960s to answer these questions. One theme built rigorous multiparameter statistical models of clusters to compare with the catalogs. The other approach looked at basic measures of clustering, mainly the two-particle correlation function, without presupposing the existence of any specific cluster form. The theory successfully began Lemaitre's program to calculate kinetic gravitational clustering in an infinite system of discrete objects - the problem whose root, we have seen, goes back to Bentley and Newton. All these developments were being stimulated by the new Lick Catalog of galaxy counts. More than a million galaxies were having their positions and magnitudes measured. Although this would supersede the catalogs of the Herschels, Dreyer, Hubble, and Shapley, its refined statistics would reveal new problems.

Neyman and Scott (1952, 1959) gambled on the idea that clusters dominate the distribution. Their model generally supposed all galaxies to be in clusters, which could, however, overlap. The centers of these clusters were distributed quasi-uniformly at random throughout space. This means that any two nonoverlapping volume elements of a given size have an equal chance of containing N cluster centers, regardless of where the volumes are. The number of cluster centers in these volume elements are independent, but the number of galaxies may be correlated, since parts of different clusters may overlap.

Within each cluster, galaxies are positioned at random subject to a radially dependent number density, which has the same form for all clusters. Thus each cluster has the same scale, unrelated to the total number of galaxies in it. This hypothesis simplified the mathematics considerably but turned out to be completely unrealistic. The total number of galaxies in each cluster was chosen randomly from a single given distribution. Finally, the motions of the galaxies and clusters were ignored.

Specifying detailed forms for these distributions then defined a particular model in terms of parameters such as the average values of the distance between cluster centers, the number of galaxies in a cluster, the size of a cluster, and the ranges of these values. Projecting models onto the sky and further assuming a luminosity function for the galaxies together with a model of interstellar obscuration (usually none for simplicity) gave the average number density and spatial moments of its fluctuating projected distribution. Comparison with observation requires the intervention of additional models that describe how photographic plates record the galaxies and how people, or machines, count them. Neither of these are straightforward, particularly when the emulsions, observing conditions, observers, and measurers are as varied as they were in the Lick Survey.

There are so many opportunities for oversimplification that any eventual agreement between these types of models and the observations becomes ambiguous. Proliferating parameters inhibit progress. Neyman and Scott (1959) realized this when they remarked "However it must be clear that the theory outlined, or any theory of this kind, somewhat comparable in spirit to the Ptolemean attempts to use sequences of epicycles in order to present the apparent motions of planets, cannot be expected to answer the more important question, why are the galaxies distributed as they actually are? The answer to this "why" even if this word is taken in (quite appropriately) quotes, may be forthcoming from studies of a novel kind, combining probabalistic and statistical considerations with those of dynamics." Although the connection of this pure cluster description with the observations was too tenuous to be convincing, and it had no connection at all with dynamical theory, it did raise the discussion to a much higher level of rigor, detail, and perception. it set the tone, if not the content, for nearly everything that followed.

The first to follow was the idea that the two-particle correlation function might provide a nearly model-independent measure of clustering. Clusters were perhaps too rigid a description of the galaxy distribution. Even though it might formally be possible to decompose any distribution into clusters, their properties would be so varied that any a priori attempt to guess them would fail. Clustering statistics, however, embody fewer preconceptions. One could hope to observe them fairly directly and eventually relate them to a dynamical theory. The two-point correlation function had recently been appropriated from turbulence theory to describe brightness fluctuations in the Milky Way (Chandrasekhar and Münch, 1952), and so it was natural to use this for describing fluctuations in the galaxy density distribution. An initial attempt (Limber, 1953, 1954) faltered on a technicality - failure to distinguish completely between a smoothed out density and a discrete point density (Neyman and Scott, 1955) - but this was soon clarified (Layzer, 1956; Limber, 1957; Neyman, 1962). The two-point correlation function remains one of the most useful galaxy clustering statistics to this day.

What is it? In a system of point galaxies (or in a smoother compressible fluid) we can define the local number (or mass) density in a volume of size V. Generally this may be regarded, after suitable normalization, as the probability for finding a galaxy in V. There will be some average probability (or density) for the entire system, but the local probability (density) usually fluctuates from place to place. The presence of galaxies in one volume may alter the probability for finding galaxies in another volume, relative to the average probability. Spatial correlation functions describe how these probabilities change with position in the system. If the system is statistically homogeneous (like cottage cheese), the correlations depend only on the relative positions of volume elements, and not on their absolute position in the system. Correlations may grow or decay with time as the structure of clustering evolves. The homogeneous two-particle correlation function is the simplest one. Given a galaxy in a volume element V₁ at any position r₁, it is the probability for finding a galaxy in another volume element V₂ a distance |r₁ - r₂| away after the uniform average probability for finding a galaxy in any volume element V has been subtracted off. This idea is not new.

Long ago, in the theory of liquids, it became clear (e.g., Kirkwood, 1935) that the presence of one molecule in a region increased the probability of finding another nearby. To express this, consider a volume of space containing N galaxies (or molecules or, generally, particles) labelled 1, 2, 3, ..., N. Denote the probability that galaxy 1 is in a specified small region dr₁ and galaxy 2 in dr₂ and so on for n of the N galaxies by Pⁿ(r₁, r₂, ... , r_n) dr₁ dr₂ ... dr_n, whatever the configuration of the remaining N - n galaxies. Since all n galaxies must be somewhere in the total volume V, the normalization for each P⁽ⁿ⁾ is

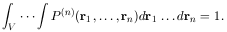(6.1)

Next, suppose we wish to designate the probability that there are n galaxies in the volume elements dr₁ . . . dr_n without specifying which galaxy is in which volume element. Then any of the N galaxies could be in dr₁, any of N - 1 in dr₂, and any of N - n + 1 in dr_n, giving a total of

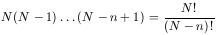(6.2)

possibilities and the general distribution function

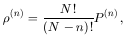(6.3)

whose normalization is

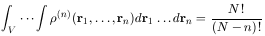(6.4)

from (6.1).

For example, ⁽¹⁾ is just the probability that some one galaxy is in dr₁ at r₁. If this is constant over the entire volume V. then

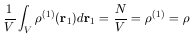(6.5)

is just the constant number density (or mass density if all particles have the same mass) as in a perfect incompressible fluid. Similarly ⁽²⁾ (r₁, r₂) dr₁dr₂ is the probability that any one galaxy is observed in dr₁ and any other in dr₂. If the distribution is statistically homogeneous on the scales of r₁₂ = |r₁ - r₂|, then it does not matter where these volume elements are and ⁽²⁾ can depend only on their separation as ⁽²⁾(r₁₂). This reduces the number of variables in ⁽²⁾ from six to one, a drastic simplification, which may, however, apply only over a restricted range of scales. It implies that any point can be considered the center of the system - as Nicholas de Cusa pointed out earlier.

To define the correlation function, we note that if the distribution is completely uncorrelated (analogous to a perfect gas), the probabilities of finding galaxies in different volume elements are independent and therefore multiply:

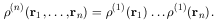(6.6)

But any correlations will introduce modifications, which we can represent by writing more generally

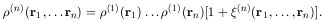(6.7)

If the general correlation function ⁽ⁿ⁾ is positive, then any n galaxies will be more clustered than a Poisson (uncorrelated) distribution; for ⁽ⁿ⁾ < 0 they are less clustered. Obviously ⁽¹⁾ - 0, and ⁽²⁾ is the two-point correlation function.

If the distribution is statistically homogeneous on scales r₁₂, then ⁽²⁾ will also depend only on r = r₁₂. When there is a galaxy at the origin r₁ = 0 then (r₁) dr₁ = 1 and the conditional probability for a galaxy to be at r₂ in dr₂ is, from (6.7),

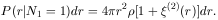(6.8)

Therefore ⁽²⁾(r) represents the excess probability, over the random Poisson probability, that there is a galaxy in a small volume element at r , given that there is a galaxy at r = 0. With statistical homogeneity, any point could be chosen as the origin, which could therefore be on any galaxy. Thus this describes clustering, without need for any well-defined clusters to exist.

Simple relations between the form of ⁽²⁾(r) and local density fluctuations provide a way to measure it observationally. Integrating (6.8) over a small volume around the origin shows that ⁽²⁾(r) must have a term equal to the Dirac delta function, (r), since there must be one point galaxy in this volume, however small. Any other terms in ⁽²⁾ must be of order or greater, since they vanish when the volume becomes so small that it can contain only 1 or 0 galaxies. Therefore we may write

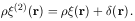(6.9)

Often (r) alone is called the two-particle correlation function, but the singular term is important because it describes the Poisson component of the fluctuations. To see this, suppose the number density in different volumes is not exactly constant but fluctuates around its average taken over the entire system (or over a much larger volume) so that = + . The average correlation for the fluctuations of all pairs of volumes with given separation, r is

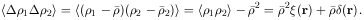(6.10)

The last equality follows from <₁ dr_{1 2} dr₂> = ₍₂₎ = dr₁ dr₂ [1 + ⁽²⁾(r₁₂)] and (6.9). Integrating over finite volumes V₁ and V₂ whose centers are a distance r apart and letting r 0 gives <( N)² 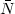> , which is the Poisson contribution for the fluctuations of N galaxies in a single finite volume. Thus, in principle, it is possible to find (r) by examining the correlations of fluctuations over different distances. In practice the problem is rather more subtle and will be examined, along with other properties of the correlation functions, in Chapters 14 and 16-20. Here I just introduce these ideas as background for our brief historical sketch.

During the early development of correlation functions in the 1950s, most astronomers regarded them just as a convenient alternative description of the observations. Gamow (1954) was the exception, and he tried to relate the fluctuations and correlations in a general way to his theory of galaxy formation from primordial turbulence. His was probably the first claim that quantitative details of the observed galaxy distribution (Rubin, 1954) supported a specific physical theory of cosmogony.

Comparison of the two-point correlation function and related theoretical statistics with observations began in earnest with the new Lick galaxy survey (Shane and Wirtanen. 1954; Shane, 1956; Shane, Wirtanen, and Steinlin, 1959). In the tradition of MayalFs (1934) earlier Lick catalog, described in Chapter 4, the new survey took a number of overlapping and duplicate photographic plates. All the sky visible from Lick was covered by 6° × 6° plates, which generally overlapped by 1°, and galaxies brighter than about 18%4 were identified and counted in 10' × 10' squares. Unfortunately the survey was not designed for precision galaxy counting; observing conditions and human measuring techniques changed from area to area. Counts in duplicated regions showed significant differences. These depended on the emulsion used; polar and zenith distances of the exposure; the seeing conditions; the apparent magnitude. type, and surface brightness of a galaxy; density of galaxies in the field; position of a galaxy on the plate; identity of the measurer; and state of the measurer. This last effect was important since a measurer, not being a machine in those days, could easily become tired or distracted. Shane is reported to have counted galaxies while talking on the telephone to prove he could do science and administration simultaneously. Attempts to correct for these effects by using the overlapping regions and averaging counts over larger areas had mixed results.

So vast was the database, however, that all these uncertainties (Scott, 1962) could not hide the existence of real clusters and the basic form of correlations. Lacking computers to analyze this database, the determination of correlations was rather crude, but even so they clearly did not fit the models dominated by clusters (Neyman and Scott, 1959). Despite a large injection of parameters, the cluster models did not survive.

The correlation functions, in their original form (Limber, 1957; Rubin, 1954), did not survive either. This was because the labor involved in a high-resolution analysis of the counts was too great to obtain (r), or its analog W() for counts in cells projected on the sky, (14.36), accurately by direct computation. Nelson Limber once mentioned to me that his calculation was done by writing the galaxy counts for cells in contiguous strips of the sky on long strips of paper, laying these out on the floors of the large Yerkes Observatory offices, shifting the strips along the floor by a distance r, and reading off the shifted counts to compute the "lag correlation" with a mechanical adding machine. To ease the work, which was compounded by the need to convolve the observed counts with models for interstellar absorption and the galaxy luminosity distribution, the form of (r) was assumed to be either exponential or Gaussian. Neither of these assumptions was correct. The discovery in 1969 that (r) is essentially a power law would begin the modern age of our understanding.

Attempts to understand the physics of clustering in the 1950s also had to contend with a fundamental doubt. The earlier disagreements over whether clusters are bound or disrupting persisted. These were stimulated by discordant velocities in small groups, and by dynamical mass estimates that greatly exceeded the luminous estimates in large clusters. Disintegration of the clusters was one possibility (Ambartsumian, 1958); large amounts of underluminous matter was the other. Currently dark matter is the generally accepted explanation, based on the extended flat rotation curves of galaxies, improved dynamical mass estimates for clusters, the agreement of gravitational clustering statistics with observations, and the hope that exotic forms of dark matter will be discovered to close the universe. But the case is not completely closed.

While the debate over how to model the galaxy distribution in terms of clusters versus correlations developed, Ulam (1954) began the first numerical computer experiments to simulate this process. He started with mass points placed at random on the integer coordinates of a very long line and, in other experiments, on a plane. These masses interacted through Newtonian gravity, represented by second-order difference equations, in a nonexpanding universe. A digital computer calculated the motions of the particles. They clustered. Numerical instabilities in these early computations, however, made their detailed results uncertain. Dynamical insight from simulations would have to wait for much more powerful computers to extend Holmberg's and Ulam's pioneering work. Meanwhile, van Albada (1960, 1961) found the first important analytical description of discrete clustering dynamics.

Unlike the earlier calculations of Jeans, Lifshitz, and Bonnor for the density of a smooth gas acting like a fluid, van Albada analyzed the gravitational instability in a system of point particles. To describe the system completely requires the N-particle distribution functions P⁽ⁿ⁾, as in (6.1), or equivalently, all the N-particle correlation functions as in (6.7). For a simpler analysis, van Albada examined how only the one-particle distribution function P⁽¹⁾) evolves if it is not affected by the local grain- iness of the gravitational field. This neglected all the higher order distributions and correlations, particularly those produced by near neighbors. Ignoring the correlations of near neighbors significantly underestimated small-scale nonlinear relaxation but made the problem tractable. This was a major achievement in itself.

With this "collisionless" approximation, van Albada derived kinetic equations for the evolution of velocity "moments" of the one-particle position and velocity distribution function F(r, v) dr dv in the expanding universe. These moments are integrals over the distribution weighted by powers of the radial and tangential velocity. An infinite number of moments are necessary to describe the distribution, but van Albada assumed that all moments with velocity powers of three or greater vanish. This implies there is no flow of kinetic energy and that the velocity distribution at low energies is symmetrical. This assumption was needed to simplify the mathematics, but unfortunately it led to a very unrealistic description of the physics. The net effect of all these simplifications was to solve a problem only slightly more fundamental than the fluid problem. Nevertheless it gave the first results that directly related the particle density perturbations to their velocity distribution and that described spherical accretion in some detail. Large forming clusters would typically acquire a dense central core with many galaxies and a more sparsely populated halo attracting galaxies from the uniform field.

Van Albada's calculation quantified and emphasized the importance of uniform initial conditions for galaxy clustering. He even speculated that this uniformity resulted from cosmic radiation pressure - discovered five years later. But all the observations, from Herschel's survey to the great Lick catalog, had emphasized the nonuniformity of the galaxy distribution. Hubble had hoped that homogeneity would appear as the spatial scale of observations increased. As the 1960s began, opinion was mixed.