The classical models of spiral galaxies were constructed using rotation velocities. In contrast, the models of elliptical galaxies were found from luminosity profiles and calibrated using central velocity dispersions or motions of companion galaxies. An overview of classical methods to construct models of galaxies is given by Perek (1962).
Problems of the structure of galaxies were a major issue at the Tartu Observatory since Öpik's (1922) work on the distance of the M31, where a simple hydrostatic model of this galaxy was constructed. This work was continued by Kuzmin who developed the major principles of galactic modelling, and applied these to calculate models of M31 and the Galaxy (Kuzmin 1943, 1952b, 1953, 1956a, b). These were first models with a continuous change of the spatial density (earlier sums of ellipsoids of constant density were used). However, individual populations of galaxies were not represented in these models, in contrast to the Schmidt (1956) model of the Galaxy where different populations were included with ellipsoids of constant density. The study of kinematic and physical properties of stellar populations was made independently. For a review of the early views on the structure of galactic populations see Oort (1958), in Tartu this problem was investigated by Rootsmäe (1961).
A natural generalisation of classical and Kuzmin models was the explicit use of major stellar populations, such as the bulge, the disk, and the halo, as well as the flat population in spiral galaxies (consisting of young stars and interstellar gas). I did my PhD work on stellar kinematics in 1955 and turned thereafter my interest to galactic modelling. My goal was twofold: first, to get more accurate mass distributions in galaxies, and second, to find physical parameters of main stellar populations in both spiral and elliptical galaxies. My assumption was that similar stellar populations (say bulges) in galaxies of different morphological type should have similar physical parameters if their constituent stars have similar age and metallicity distribution. The methodical aspects of the new multicomponent models were discussed in a series of papers in Tartu Observatory Publications (in Russian with an English summary in Einasto 1969a). The spatial (or surface) density of practically all stellar populations can be expressed by a generalised exponential law (Einasto 1970b, 1974b, a similar expression has been used independently elsewhere)
 |
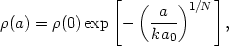(1.1) |
where
(0) = hM
/(4
a03) is the central density,
a = (R2 + z2 /
2)1/2
is the semi-major axis of the isodensity
ellipsoid, a0 is the effective (mean) radius of the
population, h and k are normalising constants, M is
the mass of the population,
is the axial ratio
of isodensity ellipsoids, and N is a
structural parameter, determining the shape of the density
profile. Here we assume that isodensity ellipsoids are concentric and
axially symmetric with a constant axial ratio for a given population.
The case N = 4 corresponds to the
de Vaucouleurs (1953)
density law for
spheroidal populations (halo), N = 1 corresponds to the classical
exponential density law, and N = 1/2 to a Gaussian density law. The
practical procedure of the model construction is the following.
First, using photometric data for galaxies the structural parameters
N of all major stellar populations are found. Next, using
colorimetric and other data mass-to-luminosity ratios of populations
are derived. Thereafter a preliminary mass distribution model is
found and the rotation (actually circular) velocity is calculated and
compared with observations. From the difference of the calculated and
observed velocity corrections to model parameters are found.
Initially these corrections were found using a trial-and-error
procedure, later an automatic computer program was developed by our
young collaborator Urmas Haud
(Einasto & Haud
1989).