4.6. The dynamo mechanism

According to the naive description of the dynamo instability presented above the origin of large-scale magnetic fields in spiral galaxies can be reduced to the following steps:

• during the 30 rotations performed by the galaxy since the protogalactic collapse, the magnetic field should be amplified by about 30 e-folds;

• if the large scale magnetic field of the galaxy is, today, (µG) the magnetic field at the onset of galactic rotation might have been even 30 e-folds smaller, i.e. (10^-19 G);

• assuming perfect flux freezing during the gravitational collapse of the protogalaxy (i.e. ) the magnetic field at the onset of gravitational collapse should be (10^-23) G over a typical scale of 1 Mpc.

This picture is oversimplified and each of the three steps mentioned above will be contrasted with the most recent findings.

The idea that a celestial body may acquire a magnetic field by differential rotation can be traced back to the paper of Larmor of 1919 [91]. One of the early ancestors of the dynamo mechanism, can be traced back to the model of Fermi and Chandrasekar [7, 8]. In [7, 8] the attempt was to connect the existence off the galactic magnetic field with the existence of a galactic angular momentum. Later on dynamo theory has been developed in greater detail (see [20]) and its possible application to large-scale magnetic fields has been envisaged.

The standard dynamo theory has been questioned in different ways. Piddington [92, 93] pointed out that small-scale magnetic fields can grow large enough (until equipartition is reached) to swamp the dynamo action. The quenching of the dynamo action has been numerically shown by Kulsrud and Anderson [94]. More recently, it has been argued that if the large-scale magnetic field reaches the critical value ⁽¹⁵⁾ R_m^-1/2 v the dynamo action could also be quenched [95, 96].

Eq. (4.29) is exact, in the sense that both and contain long and short wavelength modes. The aim of the various attempts of the dynamo theory is to get an equation describing only the "mean value" of the magnetic field. To this end the first step is to separate the exact magnetic and velocity fields as

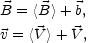(4.43)

where <> and <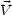> are the averages over an ensemble of many realizations of the velocity field . In order to derive the standard form of the dynamo equations few important assumptions should be made. These assumptions can be summarized as follows:

• the scale of variation of the turbulent motion 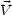should be smaller than the typical scale of variation of <>. In the galactic problem <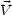> is the differential rotation of the galaxy, while 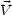is the turbulent motion generated by stars and supernovae. Typically the scale of variation of is less than 100 pc while the interesting scales for <> are larger than the kpc;

• the field 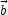is such that || << |<>|.

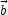• it should happen that <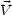 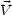^. × > 0.

• magnetic flux is frozen into the plasma (i.e. magnetic flux is conserved).

From the magnetic diffusivity equation (4.29), and using the listed assumptions, it is possible to derive the typical structure of the dynamo term by carefully averaging over the velocity field according to the procedure outlined in [19, 20, 97]. Inserting Eq. (4.43) into (4.29) and breaking the equation into a mean part and a random part, two separate induction equations can be obtained for the mean and random parts of the magnetic field

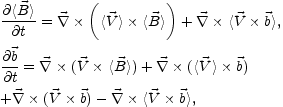(4.44) (4.45)

where the (magnetic) diffusivity terms have been neglected. In Eq. (4.44), <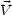 × 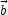> is called mean field (or turbulent) electromotive force and it is the average of the cross product of the small-scale velocity field 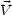and of the small scale magnetic field 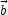over a scale much smaller than the scale of <> but much larger than the scale of turbulence. Sometimes, the calculation of the effect of <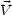 × 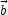> is done in the case of incompressible and isotropic turbulence. In this case <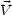 × 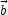> = 0. This estimate is, however, not realistic since <> is not isotropic. More correctly [97], <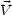 × 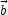> should be evaluated by using Eq. (4.45) which is usually written in a simplified form

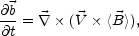(4.46)

where all but the first term of Eq. (4.45) have been neglected. To neglect the term × (<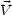> × 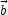) does not pose any problem since it corresponds to choose a reference frame where <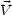> is constant. However, the other terms, neglected in Eq. (4.46), are dropped because it is assumed that |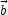| << |<>|. This assumption may not be valid all the time and for all the scales. The validity of Eq. (4.46) seems to require that is very large so that magnetic diffusivity can keep always 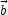small [98]. On the other hand [97] one can argue that 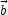is only present over very small scales (smaller than 100 pc) and in this case the approximate form of eq. (4.46) seems to be more justified.

From Eqs. (4.44)-(4.46) it is possible to get to the final result for the evolution equation of <> [97] as it is usally quoted

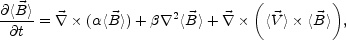(4.47)

where

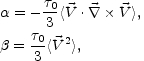(4.48) (4.49)

where is the dynamo term, is the diffusion term and ₀ is the typical correlation time of the velocity field. The term is, in general, space-dependent. The standard lore is that the dynamo action stops when the value of the magnetic field reaches the equipartition value (i.e. when the magnetic and kinetic energy of the plasma are comparable). At this point the dynamo "saturates". The mean velocity field can be expressed as <> × where |(r)| is the angular velocity of differential rotation at the galactocentric radius r. In the case of flat rotation curve |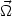(r)| = (r) ~ r^-1 which also implies that |(r)| / r < 1.

Eq. (4.47) can then be written in terms of the radial and azimuthal components of the mean magnetic field, neglecting, for simplicity, the diffusivity term:

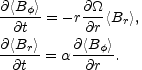(4.50) (4.51)

The second equation shows that the effect amplifies the radial component of the large-scale field. Then, through Eq. (4.50) the amplification of the radial component is converted into the amplification of the azimuthal field, this is the effect.

Usually the picture for the formation of galactic magnetic fields is related to the possibility of implementing the dynamo mechanism. By comparing the rotation period with the age of the galaxy (for a Universe with ~ 0.7, h ~ 0.65 and _m ~ 0.3) the number of rotations performed by the galaxy since its origin is approximately 30. During these 30 rotations the dynamo term of Eq. (4.47) dominates against the magnetic diffusivity. As a consequence an instability develops. This instability can be used in order to drive the magnetic field from some small initial condition up to its observed value. Eq. (4.47) is linear in the mean magnetic field. Hence, initial conditions for the mean magnetic field should be postulated at a given time and over a given scale. This initial mean field, postulated as initial condition of (4.47) is usually called seed.

Most of the work in the context of the dynamo theory focuses on reproducing the correct features of the magnetic field of our galaxy. The achievable amplification produced by the dynamo instability can be at most of 10¹³, i.e. e³⁰. Thus, if the present value of the galactic magnetic field is 10^-6 Gauss, its value right after the gravitational collapse of the protogalaxy might have been as small as 10^-19 Gauss over a typical scale of 30-100 kpc.

There is a simple way to relate the value of the magnetic fields right after gravitational collapse to the value of the magnetic field right before gravitational collapse. Since the gravitational collapse occurs at high conductivity the magnetic flux and the magnetic helicity are both conserved. Right before the formation of the galaxy a patch of matter of roughly 1 Mpc collapses by gravitational instability. Right before the collapse the mean energy density of the patch, stored in matter, is of the order of the critical density of the Universe. Right after collapse the mean matter density of the protogalaxy is, approximately, six orders of magnitude larger than the critical density.

Since the physical size of the patch decreases from 1 Mpc to 30 kpc the magnetic field increases, because of flux conservation, of a factor (_a / _b)^2/3 ~ 10⁴ where _a and _b are, respectively the energy densities right after and right before gravitational collapse. The correct initial condition in order to turn on the dynamo instability would be || ~ 10^-23 Gauss over a scale of 1 Mpc, right before gravitational collapse.

This last estimate is rather generous and has been presented just in order to make contact with several papers (concerned with the origin of large scale magnetic fields) using such an estimate. The estimates presented in the last paragraph are based on the (rather questionable) assumption that the amplification occurs over thirty e-folds while the magnetic flux is completely frozen in. In the real situation, the achievable amplification is much smaller. Typically a good seed would not be 10^-19 G after collapse (as we assumed for the simplicity of the discussion) but rather [97]

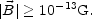(4.52)

The possible applications of dynamo mechanism to clusters is still under debate and it seems more problematic [73, 74]. The typical scale of the gravitational collapse of a cluster is larger (roughly by one order of magnitude) than the scale of gravitational collapse of the protogalaxy. Furthermore, the mean mass density within the Abell radius ( 1.5h^-1 Mpc) is roughly 10³ larger than the critical density. Consequently, clusters rotate much less than galaxies. Recall that clusters are formed from peaks in the density field. The present overdensity of clusters is of the order of 10³. Thus, in order to get the intra-cluster magnetic field, one could think that magnetic flux is exactly conserved and, then, from an intergalactic magnetic field || > 10^-9 G an intra cluster magnetic field || > 10^-7 G can be generated. This simple estimate shows why it is rather important to improve the accuracy of magnetic field measurements in the intra-cluster medium discussed in Section 3: the change of a single order of magnitude in the estimated magnetic field may imply rather different conclusions for its origin. Recent numerical simulations seem to support the view that cluster magnetic fields are entirely primordial [99].

¹⁵ v is the velocity field at the outer scale of turbulence. Back.