4.5. Magnetic diffusivity equation

From Eqs. (4.22) and (4.23) the Ohmic electric field can be expressed as

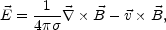(4.28)

which inserted into Eq. (4.19) leads to the magnetic diffusivity equation

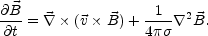(4.29)

The first term of Eq. (4.29) is the dynamo term. The second term of Eq. (4.29) is the magnetic diffusivity term whose effect is to dissipate the magnetic field. By comparing the left and the right hand side of Eq. (4.29), the typical time scale of resistive phenomena is

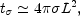(4.30)

where L is the typical length scale of the magnetic field. In a non-relativistic plasma the conductivity goes typically as T^3/2 [85]. In the case of planets, like the earth, one can wonder why a sizable magnetic field can still be present. One of the theories is that the dynamo term regenerates continuously the magnetic field which is dissipated by the diffusivity term [20]. In the case of the galactic disk the value of the conductivity ⁽¹³⁾ is given by 7 × 10^-7 Hz. Thus, for L kpc t 10⁹(L / kpc)² sec.

In Eq. (4.30) the typical time of resistive phenomena has been introduced. Eq. (4.30) can also give the typical resistive length scale once the time-scale of the system is specified. Suppose that the time-scale of the system is given by t_U ~ H₀^-1 ~ 10¹⁸ sec where H₀ is the present value off the Hubble parameter. Then

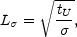(4.31)

leading to L ~ AU. The scale (4.31) gives then the upper limit on the diffusion scale for a magnetic field whose lifetime is comparable with the age of the Universe at the present epoch. Magnetic fields with typical correlation scale larger than L are not affected by resistivity. On the other hand, magnetic fields with typical correlation scale L < L are diffused. The value L ~ AU is consistent with the phenomenological evidence that there are no magnetic fields coherent over scales smaller than 10^-5 pc.

The dynamo term may be responsible for the origin of the magnetic field of the galaxy. The galaxy has a typical rotation period of 3 × 10⁸ yrs and comparing this number with the typical age of the galaxy, (10¹⁰ yrs), it can be appreciated that the galaxy performed about 30 rotations since the time of the protogalactic collapse.

From Eq. (4.29) the usual structure of the dynamo term may be derived by carefully averaging over the velocity filed according to the procedure of [89, 90]. By assuming that the motion of the fluid is random and with zero mean velocity the average is taken over the ensemble of the possible velocity fields. In more physical terms this averaging procedure of Eq. (4.29) is equivalent to average over scales and times exceeding the characteristic correlation scale and time ₀ of the velocity field. This procedure assumes that the correlation scale of the magnetic field is much bigger than the correlation scale of the velocity field which is required to be divergence-less ( ^. = 0). In this approximation the magnetic diffusivity equation can be written as:

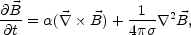(4.32)

where

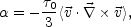(4.33)

is the so-called dynamo term which vanishes in the absence of vorticity. In Eqs. (4.32)-(4.33) is the magnetic field averaged over times longer that ₀ which is the typical correlation time of the velocity field.

It can be argued that the essential requirement for the consistence of the mentioned averaging procedure is that the turbulent velocity field has to be "globally" non-mirror symmetric [19]. If the system would be, globally, invariant under parity transformations, then, the term would simply vanish. This observation is related to the turbulent features of cosmic systems. In cosmic turbulence the systems are usually rotating and, moreover, they possess a gradient in the matter density (think, for instance, to the case of the galaxy). It is then plausible that parity is broken at the level of the galaxy since terms like _m ^. × are not vanishing [19].

The dynamo term, as it appears in Eq. (4.32), has a simple electrodynamical meaning, namely, it can be interpreted as a mean ohmic current directed along the magnetic field :

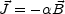(4.34)

This equation tells us that an ensemble of screw-like vortices with zero mean helicity is able to generate loops in the magnetic flux tubes in a plane orthogonal to the one of the original field. Consider, as a simple application of Eq. (4.32), the case where the magnetic field profile is given by

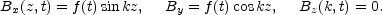(4.35)

For this profile the magnetic gyrotropy is non-vanishing, i.e. ^. × = k f²(t). From Eq. (4.32), using Eq. (4.35) f (t) obeys the following equation

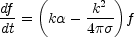(4.36)

admits exponentially growing solutions for sufficiently large scales, i.e. k < 4 || . Notice that in this naive example the term is assumed to be constant. However, as the amplification proceeds, may develop a dependence upon ||², i.e. ₀(1 - ||²) ₀[1 - f²(t)]. In the case of Eq. (4.36) this modification will introduce non-linear terms whose effect will be to stop the growth of the magnetic field. This regime is often called saturation of the dynamo and the non-linear equations appearing in this context are sometimes called Landau equations [19] in analogy with the Landau equations appearing in hydrodynamical turbulence.

In spite of the fact that in the previous example the velocity field has been averaged, its evolution obeys the Navier-Stokes equation

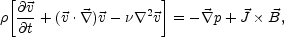(4.37)

where is the thermal viscosity coefficient. Since in MHD the matter current is solenoidal (i.e. ^.( ) = 0) the incompressible closure = 0, corresponds to a solenoidal velocity field ^. = 0. Recalling Eq. (4.22), the Lorentz force term can be re-expressed through vector identities and Eq. (4.37) becomes

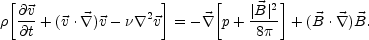(4.38)

In typical applications to the evolution of magnetic fields prior to recombination the magnetic pressure term is always smaller than the fluid pressure ⁽¹⁴⁾, i.e. p >> ||². Furthermore, there are cases where the Lorentz force term can be ignored. This is the so-called force free approximation. Defining the kinetic helicity as 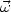= × , the magnetic diffusivity and Navier-Stokes equations can be written in a rather simple and symmetric form

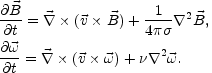(4.39)

In MHD various dimensionless ratios can be defined. The most frequently used are the magnetic Reynolds number, the kinetic Reynolds number and the Prandtl number:

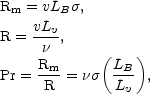(4.40) (4.41) (4.42)

where L_B and L_v are the typical scales of variation of the magnetic and velocity fields. In the absence of pressure and density perturbations the combined system of Eqs. (4.22) and (4.38) can be linearized easily. Using then the incompressible closure the propagating modes are the Alfvén waves whose typical dispersion relation is ² = c_a² k² where c_a = || / (4 )^1/2. Often the Lundqvist number is called, in plasma literature [85, 87] magnetic Reynolds number. This confusion arises from the fact that the Lunqvist number, i.e. c_a L , is the magnetic Reynolds number when v coincides with the Alfvén velocity. To have a very large Lundqvist number implies that the the conductivity is very large. In this sense the Lunqvist number characterizes, in fusion theory, the rate of growth of resistive instabilities and it is not necessarily related to the possible occurrence of turbulent dynamics. On the contrary, as large Reynolds numbers are related to the occurrence of hydrodynamical turbulence, large magnetic Reynolds numbers are related to the occurence of MHD turbulence [87].

¹³ It is common use in the astrophysical applications to work directly with = (4 )^-1. In the case of the galactic disks = 10²⁶ cm² Hz. The variable denotes, in the present review, the conformal time coordinate. Back.

¹⁴ Recall that in fusion studies the quantity = 8 ||² / p is usually defined. If the plasma is confined, then is of order 1. On the contrary, if >> 1, as implied by the critical density bound in the early Universe, then the plasma may be compressed at higher temperatures and densities. Back.