


5.2. Gauge fields in FRW Universes
In a FRW metric of the type (5.1) the evolution equations of the gauge fields are invariant under Weyl rescaling of the four-dimensional metric. This property is often named conformal invariance. Consider, for simplicity, the evolution equation of sourceless Maxwell fields:
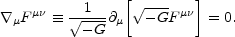 |
(5.23) |
Since the metric (5.1) is conformally flat, the time dependence arising in Eq. (5.23) from (-G)1/2, is always compensated by the controvariant indices of the fields strength. Maxwell fields in conformally flat metrics obey the same equations obtained in the case of Minkowski space-time provided the conformal time coordinate is used and provided the fields are appropriately rescaled. This property holds not only for Maxwell fields but also for chiral fermions in FRW backgrounds.
Using Weyl invariance, the generalization of MHD equations to the case of conformally flat FRW space-times can then be easily obtained:
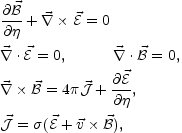 |
(5.24) (5.25) (5.26) (5.27) |
where
 |
(5.28) |
are the curved space fields expressed as a function of the corresponding flat space quantities.
In the case of a radiation dominated background, the Navier-Stokes equation takes the form
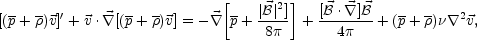 |
(5.29) |
where the incompressible closure, i.e.
 .
.  = 0,
has been already adopted and where the vector identity
= 0,
has been already adopted and where the vector identity
 ×
×
 ×
×
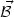 = - 1/2
= - 1/2
 |
|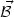 |2
+ [
|2
+ [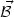 .
.
 ]
]
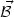 has been used.
In Eq. (5.29)
has been used.
In Eq. (5.29) 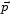 = a4 p and
= a4 p and
 =
a4
=
a4
 . In terms of
the rescaled pressure and energy densities the continuity equation becomes
. In terms of
the rescaled pressure and energy densities the continuity equation becomes
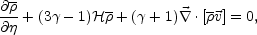 |
(5.30) |
where a barotropic equation of state has been assumed for the background
fluid, i.e.
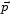 =
=

 .
The energy density is homogeneous and hence the last term in Eq. (5.30)
can be consistently dropped within the incompressible
closure. However, one may ought to linearize Eq. (5.30) and this is why
the last term may be kept for future considerations. If
.
The energy density is homogeneous and hence the last term in Eq. (5.30)
can be consistently dropped within the incompressible
closure. However, one may ought to linearize Eq. (5.30) and this is why
the last term may be kept for future considerations. If
 = 1/3,
then Eq. (5.30) implies
= 1/3,
then Eq. (5.30) implies
 ' = 0.
For generic barotropic index Eq. (5.29) becomes
' = 0.
For generic barotropic index Eq. (5.29) becomes
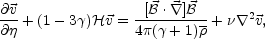 |
(5.31) |
where the magnetic pressure term has been dropped since it is negligible
with respect to
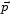 .
.
Recalling that for L >>
L the
magnetic diffusivity equation can be written, using vector identities, as
the
magnetic diffusivity equation can be written, using vector identities, as
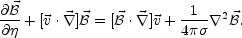 |
(5.32) |
Eqs. (5.24)-(5.29) form a closed system sharing analogies with their flat space counterpart. Thanks to conformal invariance, various solutions can be lifted from flat to curved space like, for instance [87], the following fully nonlinear solution of Eqs. (5.32) and (5.29)
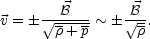 |
(5.33) |
valid if thermal and magnetic diffusivities are neglected and if
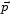 >>
|
>>
|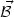 |2.
|2.
Eqs. (5.24)-(5.29) present also some differences with respect to the flat space case: since the Universe is expanding, the relative balance between diffusion scales may change as time goes by. All the propagation of MHD excitations can be then generalized to the curved-space case. In various papers [125, 126, 127, 127] this program has been achieved (see also [129, 130] for earlier attempts). In [88] the evolution of magnetic fields with non-vanishing magnetic helicity has been studied using the resistive MHD approximation in curved space. In [131] the evolution of non-linear Alfvén waves with the purpose of deriving possible observable effects [132].
In order to analyze the high-frequency spectrum of plasma excitations, the Vlasov-Landau approach can be generalized to curved spaces [133]. There are two options in order to achieve this goal. The first option is to assume that the magnetic field breaks the isotropy of space-time. This approach leads to the study of plasma effects in a magnetic field in full analogy with what is done in terrestrial tokamaks. The second choice is to discuss magnetic fields which are stochastic and which do not break the isotropy. Later in the present review the effects of magnetic fields breaking the isotropy of space-time will be considered but, for the moment, the attention will be concentrated on the second approach.
A typical problem which should be discussed within the kinetic approach is the relaxation of charge and current density fluctuations in a relativistic plasma [134]. The problem is then to compute what magnetic field is induced from charge and current density fluctuations.
Consider an equilibrium homogeneous and isotropic conducting plasma, characterized by a distribution function
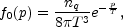 |
(5.34) |
common for both positively and negatively charged
ultrarelativistic particles (for example, electrons and positrons).
The normalization is chosen in such a way that
 d3 p f0(p) =
nq.
Within the kinetic approach, the initial charge and current density
fluctuations are related to the perturbations of the
initial value of the distribution function around the equilibrium
distribution (5.34), i.e
d3 p f0(p) =
nq.
Within the kinetic approach, the initial charge and current density
fluctuations are related to the perturbations of the
initial value of the distribution function around the equilibrium
distribution (5.34), i.e
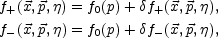 |
(5.35) |
where + refers to positrons and - to electrons, and
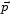 is
the conformal momentum. The Vlasov equation defining the
curved-space evolution of the perturbed distributions can be written
as
is
the conformal momentum. The Vlasov equation defining the
curved-space evolution of the perturbed distributions can be written
as
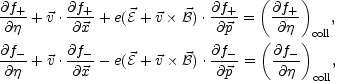 |
(5.36) (5.37) |
where the two terms appearing at the right hand side of each equation are the collision terms. This system of equation represents the curved space extension of the Vlasov-Landau approach to plasma fluctuations [82, 83]. All particle number densities here are related to the comoving volume.
Notice that, in general
 =
=
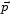 / (
/ (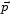 2 + me2
a2)1/2. In the ultra-relativistic limit
2 + me2
a2)1/2. In the ultra-relativistic limit
 =
=
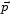 /
|
/
|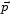 |
and the Vlasov equations are conformally invariant. This implies
that, provided we use conformal coordinates and rescaled gauge
fields, the system of equations which we would have in flat space
[84]
looks exactly the same as the one we are discussing in a
curved FRW (spatially flat) background
[133].
|
and the Vlasov equations are conformally invariant. This implies
that, provided we use conformal coordinates and rescaled gauge
fields, the system of equations which we would have in flat space
[84]
looks exactly the same as the one we are discussing in a
curved FRW (spatially flat) background
[133].
The evolution equations of the gauge fields coupled to the two Vlasov equations can be written as
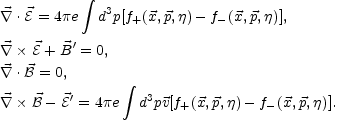 |
(5.38) |
In order to illustrate the physical relevance of this description, Eqs. (5.38) will be used later in this Section to study the fate of charge and current density fluctuations.