


6.2. Inflationary mechanisms
Different astrophysical objects, of different physical sizes, have comparable magnetic fields. This coincidence is hard to explain in the context of causal mechanisms of generation. The analogy with structure formation, already presented in the Introduction, is here useful. In the late seventies, prior to the formulation of the inflationary paradigm, the initial conditions for the density contrast were taken as primordial input. Later on, in the context of inflationary models, the primordial spectrum of curvature and density fluctuations could be calculated.
During inflation, in fact, fields of various spin are present and they can be excited by the dynamical evolution of the geometry. In the context of inflationary models of particular relevance are the scalar and tensor fluctuations of the geometry, corresponding respectively, to fluctuations of the scalar curvature and to gravitational waves. Gravitational waves and curvature perturbations obey evolution equations which are not invariant under Weyl rescaling of the four-dimensional metric. Then the quantum mechanical fluctuations in the corresponding fields will simply be amplified by the evolution of the background geometry.
It is interesting to speculate that large scale magnetic fields could be produced thanks to a similar mechanism. The major obstruction to this type of models is that gauge fields are not amplified thanks to the evolution of the background geometry the reason being that the evolution equations of gauge fields are invariant under Weyl rescaling of the metric.
When conformal invariance is broken, by some means, one is often led to estimate the amplitude of gauge field fluctuations arising as a result of the breaking. Clearly the detailed amount of amplified gauge fields will be specific of the particular model. In the following various ways of breaking conformal invariance will be listed without getting through the details of the calculations. Before doing so it is anyway instructive to introduce some general considerations stressing the analogy between the production of magnetic inhomogeneities and the production of gravitational inhomogeneities whose late time evolution leads the anisotropies in the CMB.
The tensor modes of the geometry are described by a rank-two (transverse and traceless) tensor in three spatial dimensions (25), i.e.
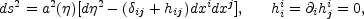 |
(6.8) |
obeying the equation, in Fourier space,
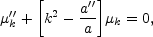 |
(6.9) |
where µk = ahk and
hk is the Fourier mode
of each polarization. In this equation the "pump field" is simply given
by the scale factor. When
k2 >> | a" / a| the mode is
said to be adiabatically damped: in fact, in this regime,
| hk|
 a-1,
i.e. decreasing in an expanding Universe. In the opposite regime, i.e.
k2 << | a" / a|
the mode is super-adiabatically amplified. In fact, during a de Sitter
or quasi-de Sitter µk ~
a(
a-1,
i.e. decreasing in an expanding Universe. In the opposite regime, i.e.
k2 << | a" / a|
the mode is super-adiabatically amplified. In fact, during a de Sitter
or quasi-de Sitter µk ~
a( )
and hk is constant. Hence, for the whole time
the given mode spends under the "potential barrier" of Eq. (6.9),
it is amplified.
)
and hk is constant. Hence, for the whole time
the given mode spends under the "potential barrier" of Eq. (6.9),
it is amplified.
A similar equation holds for the canonical normal mode for the scalar fluctuations of the geometry, i.e.
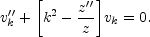 |
(6.10) |
The variable vk is defined as
 |
(6.11) |
where 
 k is
the fluctuation of the inflaton,
k is
the fluctuation of the inflaton,
 k is the
curvature perturbation and
k is the
curvature perturbation and
 is the scalar
fluctuation of the geometry in the conformally Newtonian gauge
[199,
200].
If the inflaton has an exponential potential
z(
is the scalar
fluctuation of the geometry in the conformally Newtonian gauge
[199,
200].
If the inflaton has an exponential potential
z( )
)
 a(
a( ).
).
In the case of gauge fields, each of the two polarization of the appropriately rescaled vector potential obeys, the following equation
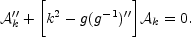 |
(6.12) |
In specific models,
g( ) may
be associated with the gauge coupling. However
g-1(
) may
be associated with the gauge coupling. However
g-1( ) can also be
viewed as a generic pump field arising as a result of the breaking
of conformal invariance. The time dependence of the potential term is
rather common to different models: it goes to zero for
|
) can also be
viewed as a generic pump field arising as a result of the breaking
of conformal invariance. The time dependence of the potential term is
rather common to different models: it goes to zero for
| |
|

 as (
as ( 2 -1/4)
2 -1/4)
 -2.
The numerical coefficient appearing in the potential
determines the strength and spectrum of the amplified gauge fields whose
subsequent evolution has to be however computed at finite conductivity.
-2.
The numerical coefficient appearing in the potential
determines the strength and spectrum of the amplified gauge fields whose
subsequent evolution has to be however computed at finite conductivity.
In Fig. 6 the typical form of the potential term
appearing in Eq. (6.12) is illustrated. Different comoving frequencies
go under the barrier at different times and the amount of amplification
is roughly proportional to the time spent under the barrier. Clearly,
given the generic form of the barrier, smaller frequencies are
more amplified than the frequencies comparable with the height of the
barrier at
 1.
In Fig. 6 the explicit numerical value of the height
of the barrier corresponds to a (present) frequency of 108 Hz
which can be realized if the pump field
goes to a constant right after the end of a conventional inflationary phase
followed by a radiation-dominated stage of expansion.
1.
In Fig. 6 the explicit numerical value of the height
of the barrier corresponds to a (present) frequency of 108 Hz
which can be realized if the pump field
goes to a constant right after the end of a conventional inflationary phase
followed by a radiation-dominated stage of expansion.
In the case of gravitational waves, and, with some caveats, in the case
of scalar
metric fluctuations, the "potential barriers" appearing, respectively,
in Eqs. (6.9) and (6.10)
may be related with the inverse Hubble radius. Hence, in the case of
metric fluctuations, a mode which is under the barrier is also, with a
swift terminology, outside the horizon (see
Fig. 7). This is the reason why, following
the conventional nomenclature, in Fig. 6 the moment
when a given scale gets under the barrier has been denoted by
 ex
(i.e. horizon exit). According to the same convention,
the moment when a given scale gets out the potential barrier is
labeled by
ex
(i.e. horizon exit). According to the same convention,
the moment when a given scale gets out the potential barrier is
labeled by
 re
(i.e. horizon re-entry).
re
(i.e. horizon re-entry).
In Fig. 6 few relevant frequencies have been
compared with the height of the barrier. Consider, for instance,
 G i.e. the
typical scale of gravitational collapse which is of the order of 1 Mpc,
i.e. 10-14 Hz.
In Fig. 6 the physical frequency has been directly
reported. Another interesting frequency is
G i.e. the
typical scale of gravitational collapse which is of the order of 1 Mpc,
i.e. 10-14 Hz.
In Fig. 6 the physical frequency has been directly
reported. Another interesting frequency is

 ~ mHz corresponding
to the present value of the magnetic diffusivity momentum.
The amplification caused by the parametric amplification of
the vacuum fluctuations can be computed by solving Eq. (6.12) in the
different regimes.
~ mHz corresponding
to the present value of the magnetic diffusivity momentum.
The amplification caused by the parametric amplification of
the vacuum fluctuations can be computed by solving Eq. (6.12) in the
different regimes.
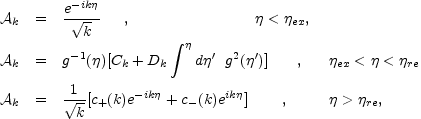 |
(6.13) |
where ( Ck, Dk, and c±(k) are integrations constants).
The mixing coefficients
c±(k), determining the
parametric amplification of a mode k2 < |
V( 1)|, computed
by matching these various branches of the solution reported in
Eq. (6.13). One finds:
1)|, computed
by matching these various branches of the solution reported in
Eq. (6.13). One finds:
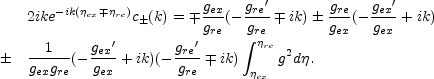 |
(6.14) |
Similar calculations can be performed in order to obtain the spectrum of scalar and tensor fluctuations of the geometry [204, 205, 206].
Suppose now to make a simple estimate. Assume, for instance,
that g is evolving prior to
 1
according to the dynamics dictated by a given model. Suppose also that
after
1
according to the dynamics dictated by a given model. Suppose also that
after
 1
the Universe is suddenly dominated by radiation, and g' ~ 0 for
1
the Universe is suddenly dominated by radiation, and g' ~ 0 for
 >
>
 1.
In this situation all the modes reenter during radiation and the
amplification will be roughly given, to leading order by
1.
In this situation all the modes reenter during radiation and the
amplification will be roughly given, to leading order by
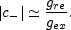 |
(6.15) |
If the function
g( ) is
identified with the evolving gauge coupling this result
suggest that in order to have large amplification,
g(
) is
identified with the evolving gauge coupling this result
suggest that in order to have large amplification,
g( ) has
to grow from smaller to larger values. This is what happens, for
instance, in the case of pre-big bang models where
g ~ e
) has
to grow from smaller to larger values. This is what happens, for
instance, in the case of pre-big bang models where
g ~ e /2 and
/2 and
 is the
for-dimensional dilaton field
[123].
is the
for-dimensional dilaton field
[123].
Since we ought to estimate the amplification of an initial quantum mechanical fluctuations, a fully quantum mechanical treatment is certainly appropriate also in view of the discussion of the correlation properties of the obtained fluctuations. This analysis has been performed in [207] where the squeezing properties of the obtained photons have also been discussed.
The perturbed effective Lagrangian density
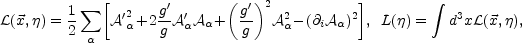 |
(6.16) |
describes the evolution of the two
( =
=
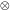 ,
,
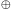 )
transverse degrees of
freedom defined by the Coulomb gauge condition A0 = 0
and
)
transverse degrees of
freedom defined by the Coulomb gauge condition A0 = 0
and  .
.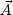 = 0
(the prime denotes differentiation with respect to conformal time). The
fields
A
= 0
(the prime denotes differentiation with respect to conformal time). The
fields
A =
g
=
g
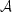
 have kinetic terms
with canonical normalization and the time evolution given
in Eq. (6.12) stems from the Euler-Lagrange equations derived from
Eq. (6.16). By functionally deriving the
the action the canonically conjugated momenta can be obtained
leading to the Hamiltonian density and to the associated Hamiltonian
have kinetic terms
with canonical normalization and the time evolution given
in Eq. (6.12) stems from the Euler-Lagrange equations derived from
Eq. (6.16). By functionally deriving the
the action the canonically conjugated momenta can be obtained
leading to the Hamiltonian density and to the associated Hamiltonian
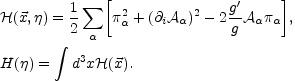 |
(6.17) |
The operators corresponding to the classical polarizations appearing in the Hamiltonian density
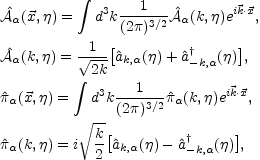 |
(6.18) |
obey canonical commutation relations and the associated
creation and annihilation operators satisfy
[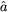 k,
k, ,
,
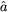 †p,
†p, ]
=
]
= 


 3(
3(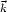 -
-
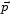 ).
).
The (two-modes) Hamiltonian contains a free part and the effect of the variation of the coupling constant is encoded in the (Hermitian) interaction term which is quadratic in the creation and annihilation operators whose evolution equations, read, in the Heisenberg picture
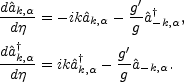 |
(6.19) |
The general solution of the previous system of equations can be written in terms of a Bogoliubov-Valatin transformation,
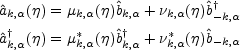 |
(6.20) |
where 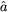 k,
k, (0) =
(0) =
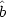 k,
k, and
and
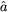 -k,
-k, =
=
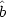 -k,
-k, .
Notice that the Bogoliubov coefficients are the quantum analog of the
mixing coefficients discussed in the semiclassical approach to the problem.
.
Notice that the Bogoliubov coefficients are the quantum analog of the
mixing coefficients discussed in the semiclassical approach to the problem.
Unitarity requires that the two complex functions
µk( ) and
) and
 k(
k( )
are subjected to the condition
|µk(
)
are subjected to the condition
|µk( )|2 -
|
)|2 -
| k(
k( )|2 = 1
which also implies that
µk(
)|2 = 1
which also implies that
µk( ) and
) and
 k(
k( ) can be
parameterized in terms of one real amplitude and two real phases
) can be
parameterized in terms of one real amplitude and two real phases
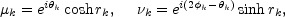 |
(6.21) |
(r is sometimes called squeezing parameter and
 k
is the squeezing phase; from now on we will drop the subscript
labeling each polarization if not strictly necessary).
The total number of produced photons
k
is the squeezing phase; from now on we will drop the subscript
labeling each polarization if not strictly necessary).
The total number of produced photons
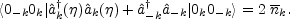 |
(6.22) |
is expressed in terms of
 k =
sin h2 rk, i.e. the mean number
of produced photon pairs in the mode k.
Inserting Eqs. (6.20)-(6.22) into Eqs. (6.19)
we can derive a closed system involving only the
k =
sin h2 rk, i.e. the mean number
of produced photon pairs in the mode k.
Inserting Eqs. (6.20)-(6.22) into Eqs. (6.19)
we can derive a closed system involving only the
 k and the
related phases:
k and the
related phases:
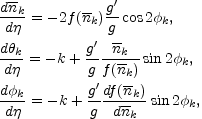 |
(6.23)
|
where
f ( k)
= [
k)
= [ k /
(
k /
( k +
1)]1/2.
k +
1)]1/2.
In quantum optics [208, 209] the coherence properties of light fields have been a subject of intensive investigations for nearly half a century. In the present context the multiparticle states described so fare are nothing but squeezed states of the electromagnetic field [208, 209]. In fact, up to now the Heisenberg description has been adopted. In the Schrödinger picture the quantum mechanical states obtained as a result of the time evolution are exactly squeezed vacuum states [208, 209].
Magnetic fields over galactic scales have typical frequency of the order 10-14-10-15 Hz which clearly fall well outside the optical range. Thus, the analogy with quantum optics is only technical. The same quantum optical analogy has been successfully exploited in particle [210] and heavy-ions physics [211] of pion correlations (in order to measure the size of the strongly interacting region) and in the phenomenological analysis of hadronic multiplicity distributions.
The interference between the amplitudes of the magnetic fields (Young interferometry [212], in a quantum optical language) estimates the first order coherence of the magnetic background at different spatial locations making use of the two-point correlation function whose trace over the physical polarizations and for coincidental spatial locations is related to the magnetic energy density. Eqs. (6.23)-(6.25) can be solved once the pump field is specified but general expressions can be also obtained [207].
6.2.1. Conventional inflationary models
In conventional inflationary models it is very difficult to produce large scale magnetic fields with phenomenologically relevant strength. This potential difficulty has been scrutinized in various investigations [202, 213, 214, 215].
Turner and Widrow [213] listed a series of field theory models in de Sitter space with the purpose of finding a natural way of breaking conformal invariance. The first suggestion was that conformal invariance may be broken, at an effective level, through the coupling of photons to the geometry [216]. Typically, the breaking of conformal invariance occurs through products of gauge-field strengths and curvature tensors, i.e.
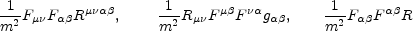 |
(6.26) |
where m is the appropriate mass scale;
Rµ

 and
Rµ
and
Rµ are
the Riemann and Ricci tensors and R is the Ricci scalar. If the
evolution of gauge fields is studied during a phase of de Sitter (or
quasi-de Sittter)
expansion, then the amplification of the vacuum fluctuations induced by the
couplings listed in Eq. (6.26) is minute. The price in order to get
large amplification should be, according to
[213],
an explicit breaking of gauge-invariance by direct coupling of the
vector potential to the Ricci tensor or to the Ricci scalar, i.e.
are
the Riemann and Ricci tensors and R is the Ricci scalar. If the
evolution of gauge fields is studied during a phase of de Sitter (or
quasi-de Sittter)
expansion, then the amplification of the vacuum fluctuations induced by the
couplings listed in Eq. (6.26) is minute. The price in order to get
large amplification should be, according to
[213],
an explicit breaking of gauge-invariance by direct coupling of the
vector potential to the Ricci tensor or to the Ricci scalar, i.e.
 |
(6.27) |
In [213] two other different models were proposed (but not scrutinized in detail) namely scalar electrodynamics and the axionic coupling to the Abelian field strength.
Dolgov [215]
considered the possible breaking of conformal invariance due
to the trace anomaly. The idea is that the conformal invariance of
gauge fields is broken by the triangle diagram where two photons in the
external lines couple to the graviton through a loop of fermions. The local
contribution to the effective action leads to the vertex
((-g)1/2)1+ F
F
 F
F
 where
where
 is a numerical
coefficient depending upon the number of scalars and fermions present
in the theory. The evolution
equation for the gauge fields, can be written, in Fourier space, as
is a numerical
coefficient depending upon the number of scalars and fermions present
in the theory. The evolution
equation for the gauge fields, can be written, in Fourier space, as
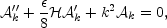 |
(6.28) |
and it can be shown that only if
 > 0 the gauge
fields are amplified. Furthermore, only is
> 0 the gauge
fields are amplified. Furthermore, only is
 ~ 8 substantial
amplification of gauge fields is possible.
~ 8 substantial
amplification of gauge fields is possible.
In a series of papers [217, 218, 219] the possible effect of the axionic coupling to the amplification of gauge fields has been investigated. The idea is here that conformal invariance is broken through the explicit coupling of a pseudo-scalar field to the gauge field (see Section 5), i.e.
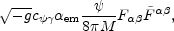 |
(6.29) |
where 

 is the dual field strength and where
c
is the dual field strength and where
c
 is a numerical factor of order one. Consider now the
case of a standard pseudoscalar potential, for instance
m2
is a numerical factor of order one. Consider now the
case of a standard pseudoscalar potential, for instance
m2
 2,
evolving in a de Sitter (or quasi-de Sitter space-time).
It can be shown, rather generically, that the vertex given in Eq. (6.29)
leads to negligible amplification at large length-scales. The coupled
system of evolution equations
to be solved in order to get the amplified field is similar to Eqs. (5.123)
already introduced in the duscussion of hypermagnetic fields
2,
evolving in a de Sitter (or quasi-de Sitter space-time).
It can be shown, rather generically, that the vertex given in Eq. (6.29)
leads to negligible amplification at large length-scales. The coupled
system of evolution equations
to be solved in order to get the amplified field is similar to Eqs. (5.123)
already introduced in the duscussion of hypermagnetic fields
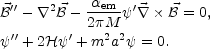 |
(6.30) (6.31) |
From Eq. (6.30), there is a maximally amplified physical frequency
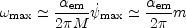 |
(6.32) |
where the second equality follows from
 ~
a-3/2 M cos mt (i.e.
~
a-3/2 M cos mt (i.e.
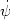 max ~ m M).
The amplification for
max ~ m M).
The amplification for  ~
~
 max is of the
order of
exp[m
max is of the
order of
exp[m em
/ (2
em
/ (2  H)]
where H is the Hubble parameter during the de Sitter phase of
expansion. From the above expressions one can
argue that the modes which are substantially amplifed are the ones for
which
H)]
where H is the Hubble parameter during the de Sitter phase of
expansion. From the above expressions one can
argue that the modes which are substantially amplifed are the ones for
which  max
>> H. The modes
interesting for the large-scale magnetic fields are the ones which are
in the opposite range, i.e.
max
>> H. The modes
interesting for the large-scale magnetic fields are the ones which are
in the opposite range, i.e.
 max <<
H.
Clearly, by lowering the curvature scale of the problem the produced
seeds may be larger and the conclusions much less pessimistic
[219].
max <<
H.
Clearly, by lowering the curvature scale of the problem the produced
seeds may be larger and the conclusions much less pessimistic
[219].
Another interesting idea pointed out by Ratra
[214]
is that the electromagnetic field may be
directly coupled to the inflaton field. In this case the coupling is
specified through a parameter
 , i.e.
e
, i.e.
e
 F
F
 F
F
 where
where
 is the
inflaton field in Planck units. In order to get
sizable large-scale magnetic fields the effective gauge coupling must be
larger than one during inflation (recall that
is the
inflaton field in Planck units. In order to get
sizable large-scale magnetic fields the effective gauge coupling must be
larger than one during inflation (recall that
 is large,
in Planck units, at the onset of inflation).
is large,
in Planck units, at the onset of inflation).
In [220] it has been suggested that the evolution of the Abelian gauge coupling during inflation induce the growth of the two-point function of magnetic inhomogeneities. This model is different from the one previously discussed [214]. Here the dynamics of the gauge coupling is not related to the dynamics of the inflaton which is not coupled to the Abelian field strength. In particular, rB(Mpc) can be as large as 10-12. In [220] the MHD equations have been generalized to the case of evolving gauge coupling. Recently a scenario similar to [220] has been discussed in [221].
In the perspective of generating large scale magnetic fields Gasperini
[222]
suggested to consider the possible mixing between the photon and the
graviphoton field appearing in supergravity theories (see also, in a
related context
[223]).
The graviphoton is
the massive vector component of the gravitational supermultiplet and its
interaction with the photon is specified by an interaction term of the
type  Fµ
Fµ Gµ
Gµ where Gµ
where Gµ is the filed strength of the massive vector. Large-scale magnetic fields
with rB(Mpc)
is the filed strength of the massive vector. Large-scale magnetic fields
with rB(Mpc)  10-34 can be obtained
if
10-34 can be obtained
if  ~
~
 (1) and for a mass of the
vector m ~ 102 TeV.
(1) and for a mass of the
vector m ~ 102 TeV.
Bertolami and Mota [224] argue that if Lorentz invariance is spontaneously broken, then photons acquire naturally a coupling to the geometry which is not gauge-invariant and which is similar to the coupling considered in [213].
Finally Davis and Dimopoulos [225] considered the possibility of phase transitions taking place during inflation. They found that sizable large-scale magnetic fields can be generated provided the phase transition occurs in the last 5 e-foldings of the inflationary stage of expansion.
While the coupling of electromagnetic field to the metric and to the charged fields is conformally invariant, the coupling of the charged scalar field to gravity is not. Thus, vacuum fluctuations of the charged scalar field can be amplified during inflation at super-horizon scales, leading potentially to non-trivial correlations of the electric currents and charges over cosmological distances. The fluctuations of electric currents, in turn, may induce magnetic fields through Maxwell equations at the corresponding scales. The role of the charged scalar field may be played by the Higgs boson which couples to the hypercharge field above the electroweak phase transition; the generated hypercharged field is converted into ordinary magnetic field at the temperatures of the order of electroweak scale.
No detailed computations were carried out in [213] in order to substantiate this idea. The suggestion of [213] was further developed quite recently in [226] for the standard electroweak theory with an optimistic conclusion that large scale magnetic fields can be indeed generated. In [227] a supersymmetric model was studied. In [134], previous treatments have been further scrutinized by computing, with higher accuracy, the amplification of the charged scalar field and the damping induced by the conductivity. It turns out that the resulting magnetic fields are insufficient in order to provide reasonable seeds for the dynamo amplification.
Introducing appropriately rescaled fields the action of the Abelian-Higgs model in a conformally flat FRW space-time can be written as
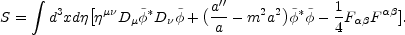 |
(6.33) |
Now, since the evolution equation of the charged scalar is not conformally invariant, current density and charge density fluctuations will be induced. Then, by employing a Vlasov-Landau description similar to the one introduced in Section 5, the resulting magnetic field will be of the order of Bdec ~ 10-40 Tdec2 which is, by far, too small. Later it has been proposed that much larger magnetic fields may be obtained in the context of the Abelian-Higgs model [228] (see however [229] for a detailed criticism of this proposal).
If internal dimensions are dynamical, then Weyl invariance
may be naturally broken
[230].
Consider a pure electromagnetic fluctuation decoupled
from the sources, representing an electromagnetic wave propagating
in the d-dimensional external space such that
Aµ  Aµ(
Aµ( ,
,
 ),
Aa = 0. In the metric given in Eq. (5.1) the evolution
equation of the gauge field fluctuations can be written as
),
Aa = 0. In the metric given in Eq. (5.1) the evolution
equation of the gauge field fluctuations can be written as
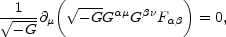 |
(6.34) |
where F
 =
=
 [
[ A
A ] is the gauge field strength and
G is the determinant of the D dimensional metric. Notice that
if n = 0 the space-time is isotropic and, therefore, the Maxwell's
equations can be reduced (by trivial rescaling) to the flat space
equations.
If n
] is the gauge field strength and
G is the determinant of the D dimensional metric. Notice that
if n = 0 the space-time is isotropic and, therefore, the Maxwell's
equations can be reduced (by trivial rescaling) to the flat space
equations.
If n  0 we have that
the evolution equation of the electromagnetic fluctuations propagating
in the external d-dimensional manifold will receive a
contribution from the internal dimensions which cannot be rescaled away
[233]
(26).
In the radiation gauge (A0 = 0 and
0 we have that
the evolution equation of the electromagnetic fluctuations propagating
in the external d-dimensional manifold will receive a
contribution from the internal dimensions which cannot be rescaled away
[233]
(26).
In the radiation gauge (A0 = 0 and
 i
Ai = 0)
(27) the evolution the
vector potentials can be written as
i
Ai = 0)
(27) the evolution the
vector potentials can be written as
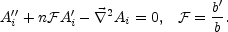 |
(6.35) |
The vector potentials Ai are already rescaled with
respect to the (conformally flat) d + 1 dimensional metric.
In terms of the canonical normal modes of oscillations
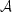 i =
bn/2 Ai
the previous equation can be written in a simpler form, namely
i =
bn/2 Ai
the previous equation can be written in a simpler form, namely
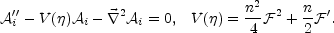 |
(6.36) |
In order to estimate the amplification of the gauge fields induced by the
evolution of the internal geometry we shall consider the background
metric of Eq. (5.13) in the case of maximally symmetric subspaces
 ij
=
ij
=  ij,
ij,
 ab
=
ab
=  ab.
ab.
Suppose now that the background geometry evolves along three different
epochs. During the first phase (taking place for
] -  ,
-
,
-  1])
the evolution is truly multidimensional. At
1])
the evolution is truly multidimensional. At
 =
-
=
-  1 the
multidimensional dynamics is continuously matched
to a radiation dominated phase turning, after decoupling, into
a matter dominated regime of expansion. During the radiation and matter
dominated stages the internal dimensions are fixed to their (present)
constant size in order not
to conflict with possible bounds arising both at the BBN time and
during the matter-dominated epoch.
The evolution of the external dimensions does not affect the amplification
of the gauge fields as it can be argued from Eq. (6.36) :in the limit
n
1 the
multidimensional dynamics is continuously matched
to a radiation dominated phase turning, after decoupling, into
a matter dominated regime of expansion. During the radiation and matter
dominated stages the internal dimensions are fixed to their (present)
constant size in order not
to conflict with possible bounds arising both at the BBN time and
during the matter-dominated epoch.
The evolution of the external dimensions does not affect the amplification
of the gauge fields as it can be argued from Eq. (6.36) :in the limit
n 0
(i.e. conformally invariant background) Eq. (6.36) reduces to the flat
space equation. A background with the features described
above has been introduced in Eq. (5.14).
Defining, respectively, bBBN
and b0 as the size of the internal dimensions at the BBN
time and at the present epoch, the maximal variation
allowed to the internal scale factor from the BBN time
can be expressed as bBBN / b0 ~ 1 +
 where
|
where
| | <
10-2
[116,
117,
118].
The bounds on the variation
of the internal dimensions during the matter dominated epoch
are even stronger. Denoting with an over-dot the derivation with
respect to the cosmic time coordinate, we have that
|
| <
10-2
[116,
117,
118].
The bounds on the variation
of the internal dimensions during the matter dominated epoch
are even stronger. Denoting with an over-dot the derivation with
respect to the cosmic time coordinate, we have that
|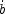 / b| <
10-9H0
where H0 is the present value of the Hubble parameter
[116].
The fact that the time evolution of internal dimensions is so tightly
constrained for temperatures lower of 1 MeV does not forbid that they
could have been dynamical prior to that epoch
[231].
/ b| <
10-9H0
where H0 is the present value of the Hubble parameter
[116].
The fact that the time evolution of internal dimensions is so tightly
constrained for temperatures lower of 1 MeV does not forbid that they
could have been dynamical prior to that epoch
[231].
In the parameterization of Eq. (5.14)
the internal dimensions grow (in conformal time) for
 < 0 and they
shrink (28) for
< 0 and they
shrink (28) for
 > 0.
> 0.
By inserting this background into Eq. (6.36) we obtain that
for  <
-
<
-  1
1
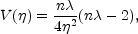 |
(6.37) |
whereas V( )
)
 0 for
0 for
 >
-
>
-  1.
Since V(
1.
Since V( )
goes to zero for
)
goes to zero for

 ±
±
 we can define, in both limits, a Fourier expansion of
we can define, in both limits, a Fourier expansion of
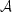 i in terms of two
distinct orthonormal sets of modes. The amplification of the quantum
mechanical fluctuations of the gauge fields can then be computed using
the standard techniques (see, for instance,
[234,
235,
236]).
In [230]
it has been shown that in simple models of dimensional decoupling
magnetic fields can be generated with strength compatible
with the bound of Eq. (6.2). In particular there is the
interesting possibility that large-scale magnetic fields are produced
in the case when internal dimensions also expand while the external ones
also expand but at a different rate.
i in terms of two
distinct orthonormal sets of modes. The amplification of the quantum
mechanical fluctuations of the gauge fields can then be computed using
the standard techniques (see, for instance,
[234,
235,
236]).
In [230]
it has been shown that in simple models of dimensional decoupling
magnetic fields can be generated with strength compatible
with the bound of Eq. (6.2). In particular there is the
interesting possibility that large-scale magnetic fields are produced
in the case when internal dimensions also expand while the external ones
also expand but at a different rate.
It should be mentioned that the interplay between gauge fields and large (or infinite) extra-dimensions is still under investigation. There is, at the moment, no definite model leading to the generation of large-scale magnetic field in a framework of infinite internal dimensions. The main reason is that it is difficult to build reasonable cosmological models with large extra-dimensions. More specifically, one would like to have a model where gauge fields arise naturally in the bulk. In six- dimensions interesting models can be constructed [239] where localized gauge zero modes may be naturally present (in analogy with what happens in the case of six-dimensional warped models [240, 241]).
6.2.4. String cosmological models
Large scale magnetic fields may also be produced in the context of
string cosmological models
[202,
289] (see also
[238]
for the analysis of the amplification of magnetic fields during a phase
of coherent dilaton oscillations
(29)).
In many respects the case of string cosmological models is related to
the one where the gauge coupling is dynamical. However, in the string
cosmological context, the dynamics of the gauge coupling and of the
geometry are connected by the solutions of the low-energy
 -functions.
The basic evolution of the background and of the gauge coupling has been
discussed in Section 5. In order to achieve
a large amplification of the quantum fluctuations of the gauge fields,
the gauge coupling should be sufficiently small when the typical scale
of the gravitational collapse hits the "potential barrier". In particular,
gex(
-functions.
The basic evolution of the background and of the gauge coupling has been
discussed in Section 5. In order to achieve
a large amplification of the quantum fluctuations of the gauge fields,
the gauge coupling should be sufficiently small when the typical scale
of the gravitational collapse hits the "potential barrier". In particular,
gex( G) < 10-33 is the dynamo
requirement has to be satisfied.
It is difficult to produce large scale magnetic fields with reasonable
amplitudes if the pre-big bang phase matches immediately to the
post-big bang evolution
[237].
However, phenomenologically
consistent pre-big bang models lead to a sufficiently long stringy
phase when the dilaton and the curvature scale are
roughly constant. If this phase is included the conditions expressed by
Eqs. (6.1) and (6.2) are easily satisfied. Furthermore, there are
regions in the parameter space of the model where
rB(
G) < 10-33 is the dynamo
requirement has to be satisfied.
It is difficult to produce large scale magnetic fields with reasonable
amplitudes if the pre-big bang phase matches immediately to the
post-big bang evolution
[237].
However, phenomenologically
consistent pre-big bang models lead to a sufficiently long stringy
phase when the dilaton and the curvature scale are
roughly constant. If this phase is included the conditions expressed by
Eqs. (6.1) and (6.2) are easily satisfied. Furthermore, there are
regions in the parameter space of the model where
rB( G) ~ 10-8
which implies that the galactic magnetic field may be fully primordial
[202,
289],
i.e. no dynamo action will be required.
G) ~ 10-8
which implies that the galactic magnetic field may be fully primordial
[202,
289],
i.e. no dynamo action will be required.
25 The theory of cosmological perturbations is assumed in the following considerations. Comprehensive accounts of the relevant topics can be found in [199, 200] (see also [201]). Back.
26 Notice that the electromagnetic field couples only to the internal dimensions through the determinant of the D-dimensional metric. In string theories, quite generically, the one-form fields are also coupled to the dilaton field. This case has been already analyzed in the context of string inspired cosmological scenarios and will be discussed later. Back.
27 For a discussion of gauges in curved spaces see [232]. Back.
28 To assume
that the internal dimensions
are constant during the radiation and matter dominated
epoch is not strictly necessary. If
the internal dimensions have a time variation during the radiation
phase we must anyway impose the BBN bounds on their variation
[116,
117,
118] .
The tiny variation allowed by BBN implies that
b( ) must be
effectively constant for practical purposes.
Back.
) must be
effectively constant for practical purposes.
Back.
29 The possible production of (short scale) magnetic fields by parametric resonance explored in [238] , has been subsequently analyzed in the standard inflationary contex [203] Back.