


6.1. Inhomogeneous MHD equations
The first attempts in this direction have been made by Biermann [187] and Harrison [189, 190, 191]. The Biermann battery mechanism is easy to understand from the form of the generalized Ohm law discussed in Eq. (4.17). MHD equations are linear and homogeneous in the magnetic field intensities. The idea is then to look for a natural source term which seemed to be provided by the thermoelectric current already introduced in the context of the generalized Ohm law . Consider, indeed, Eq. (4.17) in the approximation where the Hall term is neglected (the argument can be also generalized to the case of non vanishing Hall term). Then, the Ohmic electric field will not be the one simply obtained in resistive MHD but it will get a contribution from the thermoelectric term:
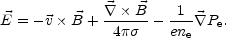 |
(6.3) |
Using the other MHD equations in the incompressible approximation the new form of the magnetic diffusivity equation can be derived:
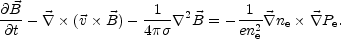 |
(6.4) |
The magnetic diffusivity equation has now a source terms which does not vanish provided the gradients of the charge density of the electrons is not parallel to the pressure gradients. As a consequence of the presence of the source term, the magnetic field will grow linearly in time until the thermoelectric source term is comparable with the dynamo term. The estimate of the magnetic field intensity prior to the onset of galactic rotation will then be
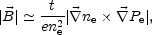 |
(6.5) |
leading to magnetic fields
 (10-20) G over
typical scales of the order of 10 kpc (see also
[188]
for a recent analysis in a similar framework).
(10-20) G over
typical scales of the order of 10 kpc (see also
[188]
for a recent analysis in a similar framework).
In a complementary perspective, Harrison
[189,
190,
191]
discussed the possibility that the pressure gradients are strictly
vanishing,
i.e.  pe = 0. This is a reasonable assumption, for instance,
in a radiation-dominated stage of expansion where pressure gradients are
expected to be negligible by the global homogeneity
of the background. In this situation, an evolution equation
for the vorticity can be derived
pe = 0. This is a reasonable assumption, for instance,
in a radiation-dominated stage of expansion where pressure gradients are
expected to be negligible by the global homogeneity
of the background. In this situation, an evolution equation
for the vorticity can be derived
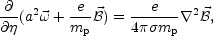 |
(6.6) |
where  =
=
 ×
×
 and
mp is the ion mass.
If we now postulate that some vorticity was present prior to decoupling,
then Eq. (6.6) can be solved and the magnetic field can be related to
the initial vorticity as
and
mp is the ion mass.
If we now postulate that some vorticity was present prior to decoupling,
then Eq. (6.6) can be solved and the magnetic field can be related to
the initial vorticity as
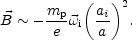 |
(6.7) |
It is clear that if the estimate of the vorticity is made prior to
equality (as originally suggested by Harrison
[189])
of after decoupling as also suggested, a bit later
[192]
can change even by two orders of magnitude. Prior to equality
|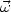 (t)|
(t)|
 0.1 / t and,
therefore,
|
0.1 / t and,
therefore,
| eq| ~
10-21 G. If a similar estimate is made after decoupling the
typical value of the generated magnetic field is of the order of
10-18 G. So, in this context, the
problem of the origin of magnetic fields is circumvented by postulating
an appropriate form of vorticity whose origin must be explained.
eq| ~
10-21 G. If a similar estimate is made after decoupling the
typical value of the generated magnetic field is of the order of
10-18 G. So, in this context, the
problem of the origin of magnetic fields is circumvented by postulating
an appropriate form of vorticity whose origin must be explained.
The idea was employed, later on, in the context of the physics of topological defects. Vachaspati and Vilenkin [193] have suggested that cosmic strings with small scale structure may be a source of the wanted vorticity. The argument is, in short, that since matter flow in baryonic wakes is turbulent, velocity gradients will be induced in the flow by the small-scale wiggles which produced the required vorticity. Furthermore, dynamical friction between cosmic strings and matter may provide a further source of vorticity [194]. There have been also studies trying to generate large-scale magnetic fields in the context of superconducting cosmic strings (see, for instance, [195] and references therein).
Recently the possible generation of large-scale magnetic fields prior to hydrogen recombination has been discussed in [196, 197]. The vorticity required in order to produce the magnetic fields is generated, according to [196], by the photon diffusion at second order in the temperature fluctuations. In a similar perspective Hogan [198] got much less optimistic estimates which, according to [196, 197], should be attributed to different approximation schemes employed in the analysis.