In the context of various mechanisms, the magnetic fields generated at large at the scale of the protogalactic collapse may be rather small. In this Section the possible effects of magnetic present over much smaller length-scales will be analyzed. Two important scales are the Hubble radius at the electroweak epoch and at the big-bang nucleosynthesis epoch.
Hypermagnetic fields present for temperatures
T 
100 GeV
have a twofold effect:
The physical picture of the possible effects of magnetic fields on the electroweak phase diagram is exactly the same as the macroscopic description of superconductors in the presence of an external magnetic field. The normal-superconducting phase transition, being of second order in the absence of magnetic fields, becomes of first order if a magnetic field is present. The reason for this is the Meissner effect, i.e. the fact that the magnetic field cannot propagate inside a superconducting cavity, and, therefore, creates an extra pressure acting on the normal-superconducting boundary. Our consideration below explores this simple picture.
Consider the plain domain wall that separates broken and symmetric phase at some temperature T, in the presence of a uniform hypercharge magnetic field Yj. Far from the domain wall, in the symmetric phase, the non-Abelian SU(2) field strength (Wj3) is equal to zero, because of a non-perturbative mass gap generation. Inside the broken phase, the massive Zj combination of Yj and W3j,
 |
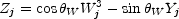(7.1) |
must be equal to zero, while the massless combination, corresponding
to photon Ajem, survives. The matching of
the fields on the boundary gives Aemj =
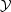j
cos
W. Thus, an
extra pressure 1/2 |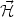
Y|2 sin2
W
acts on the domain wall from the symmetric side. At the critical
temperature it must be compensated by the vacuum pressure of the
scalar field. If we neglect loop corrections associated with the
presence of magnetic fields, then the condition that determines the
critical temperature is:
 |
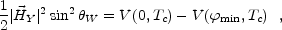(7.2) |
where V(
,
T) is the effective potential in the absence of
magnetic field,
min
is the location of the minimum of the potential at temperature T.
The above consideration was dealing with the uniform magnetic fields. Clearly, it remains valid when the typical distance scale of inhomogeneities of the magnetic field are larger than the typical bubble size. This is the case for bubbles smaller than the magnetic diffusion scale, and, in particular, at the onset of the bubble nucleation. Thus, the estimate of the critical temperature coming from (7.2) is applicable. For bubbles larger than the diffusivity scale, the presence of a stochastic magnetic field will considerably modify their evolution. In particular, the spherical form of the bubbles is very likely to be spoiled.
These considerations were presented in
[163].
Later [261]
perturbative estimates were performed in order to corroborate the proposed
picture. In
[262]
a full non-perturbative analysis
of the phhase diagram of the electroweak theory in the presence of an
hyermagnetic background has been performed. As previously discussed
[253,
254]
for values of the Higggs boson mass larger than the W boson mass
the electroweak phase diagram seems to exhibit a cross-over regime.
The inclusion of a constant hypermagnetic background with typical
strength
|
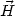Y|
/ T2
0.3 does modify the
electroweak phase diagram but does not seem to make the phase transition
strongly first order for mH
mW as
expected from perturbative considerations. Furthermore for
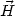|Y|
/ T2 > 0.3 (but
still compatible with the critical density bound)
a new (inhomogeneous) phase has been observed. The analysis performed in
[262]
included a net hypermagnetic flux. It would be
interesting to repeat the same calculation in the presence of a
non-vanishing hypermagnetic helicity (or gyrotropy).
Depending upon the topology of the flux lines, hypermagnetic fields can have two distinct effects:
topologically non-trivial configurations of the hypermagnetic flux lines lead to the formation of hypermagnetic knots whose decay might seed the Baryon Asymmetry of the Universe (BAU);
even if the electrowak plasma has vanishing
hypermagnetic gyrotropy, i.e.
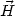<Y
.
×
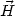Y> =
0, matter-antimatter fluctuations may be generated.
Consider first the situation where the electroweak plasma contains, for T > Tc a network of hypermagnetic knots of the type of the ones described in Eqs. (5.113)-(5.116). In Section 5 these configurations have been named hypermagnetic knots (HK) and they are Chern-Simons condensates carrying a non-vanishing (averaged) hypermagnetic helicity. As discussed, HK can be dynamically generated from a background of hypermagnetic fields with trivial topology provided a (time-dependent) pseudo-scalar is present in the plasma (see, for instance, Eq. (5.120)).
In order to seed the BAU a network of HK should be present at high temperatures. In fact for temperatures larger than Tc the fermionic number is stored both in HK and in real fermions. For T < Tc, the HK should release real fermions since the ordinary magnetic fields (present after EW symmetry breaking) do not carry fermionic number. If the EWPT is strongly first order the decay of the HK can offer some seeds for the BAU generation. This last condition can be met in the minimal supersymmetric standard model (MSSM).
The integration of the U(1)Y anomaly equation gives the CS number density carried by the HK which is in turn related to the density of baryonic number nB for the case of nf fermionic generations. In fact, using Eqs. (5.109)-(5.111) and after some algebra [163, 172] it can be shown that
 |
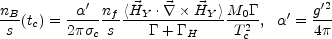(7.3) |
(g' is the U(1)Y coupling and
s = (2/45) 
2
g* T3
is the entropy density; g*, at
Tc, is 106.75 in the MSM;
M0 = MP / 1.66
(g*)1/2).
In Eq. (7.3) 
is the
perturbative rate of the right electron chirality flip processes (i.e.
scattering of right electrons with the Higgs and gauge bosons and with
the top quarks because of their large Yukawa coupling) which
are the slowest reactions in the plasma and
 |
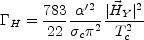(7.4) |
is the rate of right electron dilution induced by the presence of a
hypermagnetic field. In the MSM we have that
<
H
whereas in the MSSM
can naturally
be larger than
H.
Unfortunately, in the MSM
a hypermagnetic field can modify the phase diagram of the phase transition
but cannot make the phase transition strongly first order for large
masses of the Higgs boson. Therefore, we will concentrate on the case
>
H and we
will show that in the opposite limit the BAU will be anyway small
even if some (presently unknown) mechanism would make the EWPT strongly
first order in the MSM.
It is interesting to notice that, in this scenario, the value of the BAU is determined by various particle physics parameters but also by the ratio of the hypermagnetic energy density over the energy density sitting in radiation during the electroweak epoch.
Consider now the complementary situation where the electroweak plasma,
for T > Tc,
is filled with topologically trivial hypermagnetic fields. In this
case, fluctuations in the baryon to entropy ratio
will be induced since, in any case
<(Y
.
× Y)2>
0.
These fluctuations are of isocurvature type and can be related to
the spectrum of hypermagnetic fields at the EWPT. Defining as
 |
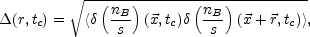(7.5) |
the fluctuations in the ratio of baryon number density
nB to the entropy density s
at t = tc
[164], the value of
(r,
tc) can be related to the hypermagnetic spectrum
which is determined in terms of its amplitude
and its slope
.
A physically realistic situation corresponds to the case in
which the Green's functions of the magnetic hypercharge fields decay at
large distance (i. e.
> 0) and this would
imply either "blue"(
0 ) or "violet"
( >> 1) energy
spectra. The fluctuations of the baryon to entropy ratio generated
at the electroweak epoch may survive until the BBN epoch
[164].
The possibility of survival of these fluctuations is related
to their typical scale which must exceed the neutron
diffusion scale appropriately blue-shifted at the
electroweak epoch. The implications of these fluctuations will
be discussed in a moment.