


7.2. Big-bang nucleosynthesis epoch
Large scale magnetic fields possibly present at the BBN epoch can have an impact on the light nuclei formation. By reversing the argument, the success of BBN can be used in order to bound the magnetic energy density possibly present at the time of formation of light nuclei. Magnetic fields, at the BBN epoch may have four distinct effects:
they can enhance the rate of the Universe expansion
at the corresponding epoch in a way proportional to
 B;
B;
they can affect the reaction rate in a way
proportional
to  em
em
 B;
B;
they can affect the phase space of the electrons;
they can induce, prior to the formation of the light nuclei, matter-antimatter fluctuations.
While the first three effects are direct, the fourth effect is mainly caused by hypermagnetic fields present even before BBN.
The idea that magnetic fields may increase the Universe
expansion and, consequently, affect directly the abundance
of 4He (which is
directly sensitive to the expansion rate) has been
pointed out long ago by Greenstein
[264] and
by Matese and O'Connel
[265].
From a qualitative point of view the effects over the expansion
should be leading in comparison with the
effects over the rate of interactions (which are suppressed by
 em).
em).
Thanks to detailed numerical simulations performed indipendently by different groups (i.e. Cheng et al. [266, 267]; Kernan, Starkman and Vachaspati [268, 269]; Grasso and Rubinstein [270, 271]), the common opinion is that the Universe expansion is the leading effect even if this conclusion has been reached only recently and not without some disagreements on the details of the calculations (see, for instance, [269]).
In order to prevent the Universe from expanding too fast at the BBN epoch
 B <
0.27
B <
0.27
 where
where

 is the
energy density contributed by the standard three light neutrinos with
masses much smaller than the MeV. The BBN bound is physically relevant
in many situations since it is a bit more constraining than the critical
density bound.
is the
energy density contributed by the standard three light neutrinos with
masses much smaller than the MeV. The BBN bound is physically relevant
in many situations since it is a bit more constraining than the critical
density bound.
The BBN bounds discussed so far are derived assuming a stochastic magnetic field at the BBN epoch. This means that the isotropy of the geometry is not affected. However, it is not unreasonable to think of the possibility that a magnetic field with a preferred direction may break the isotropy of the background. Thus bounds on the isotropy of the expansion at the BBN epoch may be turned into bounds on the shear induced by the presence of a magnetic field (see, for instance, [272, 273] and [274, 275]).
Let us now come to the last point. The matter-antimatter fluctuations created at the electroweak epoch thanks to the presence of hypermagnetic fields may survive down to the epoch of BBN. Since the fluctuations in the baryon to entropy ratio are, in general, not positive definite, they will induce fluctuations in the baryon to photon ratio, at the BBN epoch. The possible effect of matter-antimatter fluctuations on BBN depends on the typical scale of of the baryon to entropy ratio at the electroweak epoch. Recalling that for T ~ Tc ~ 100 GeV the size of the electrowek horizon is approximately 3 cm, fluctuations whose scale is well inside the EW horizon at Tc have dissipated by the BBN time through (anti)neutron diffusion. The neutron diffusion scale at Tc is
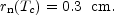 |
(7.6) |
The neutron diffusion scale
at T = 1 keV is 105 m, while, today
it is 10-5 pc, i.e. of the order of the astronomical unit.
Matter-antimatter fluctuations smaller than 105 m annihilate
before neutrino decoupling and have no effect on BBN.
Two possibilities can then be envisaged. We could require that the
matter-antimatter fluctuations (for scales
r  rn)
are small. This will then imply a
bound, in the (
rn)
are small. This will then imply a
bound, in the ( ,
,
 ) plane on the strength
of the hypermagnetic background.
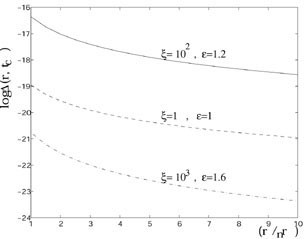
In Fig. 8 some typical baryon number fluctuations
have been reported for different choices of the parameters
) plane on the strength
of the hypermagnetic background.
In Fig. 8 some typical baryon number fluctuations
have been reported for different choices of the parameters
 and
and
 .
In Fig. 9
such an exclusion plot is reported with the full line. With the dashed
line the bound implied by the increase in the expansion rate
(i.e.
.
In Fig. 9
such an exclusion plot is reported with the full line. With the dashed
line the bound implied by the increase in the expansion rate
(i.e.  H
< 0.2
H
< 0.2
 ) is
reported. Finally with the dot-dashed line the critical density bound is
illustrated for the same hypermagnetic background.
) is
reported. Finally with the dot-dashed line the critical density bound is
illustrated for the same hypermagnetic background.
 |
 |
Figure 8. The value of the baryon number
fluctuations for different parameters of the hypermagnetic
background |
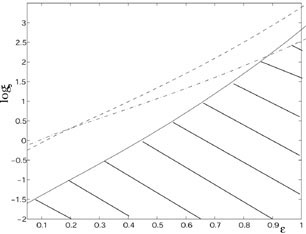 |
Figure 9. The parameter space of the
hypermagnetic background in the case
|
The second possibility is to study the effects
of large matter-matter domains.
These studies led to a slightly different scenario of BBN
[276],
namely BBN with matter-antimatter regions. This analysis has been
performed in a series of papers by Rehm and Jedamzik
[277,
282]
and by Kurki-Suonio and Sihvola
[278,
279] (see also
[280,
281]).
The idea is to discuss BBN in the presence of spherically symmetric regions
of anti-matter characterized by their radius rA and by
the parameter R, i.e. the matter/antimatter ratio.
Furthermore, in this scenario the net baryon-to-photon
ratio, 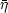 , is
positive definite and non zero.
Antimatter domains larger than 105 m at 1 keV may survive
until BBN and their dissipation has been analyzed in detail
[279].
Antimatter domains in the range
, is
positive definite and non zero.
Antimatter domains larger than 105 m at 1 keV may survive
until BBN and their dissipation has been analyzed in detail
[279].
Antimatter domains in the range
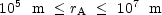 |
(7.7) |
at 1 keV annihilate before BBN for temperatures between 70 keV and 1 MeV. Since the antineutrons annihilate on neutrons, the neutron to proton ratio gets smaller. As a consequence, the 4He abundance gets reduced if compared to the standard BBN scenario. The maximal scale of matter-antimatter fluctuations is determined by the constraints following from possible distortions of the CMB spectrum. The largest scale is of the order of 100 pc (today), corresponding to 1012 m at 1 keV.
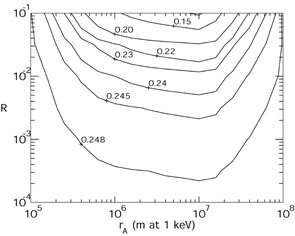 |
Figure 10. From
[283] the
4He yield is illustrated
in the (R, rA) plane for
|
Suppose that matter-antimatter regions are present in the range of Eq. (7.7). Then the abundance of 4He get reduced. The yield of 4He are reported as a function of R, the matter-antimatter ratio and rA. Now, we do know that by adding extra-relativistic species the 4He can be increased since the Universe expansion gets larger. Then the conclusion is that BBN with matter-antimatter domains allows for a larger number of extra-relativistic species if compared to the standard BBN scenario. This observation may have implications for the upper bounds on the stochastic GW backgrounds of cosmological origin [283] since the extra-relativistic species present at the BBN epoch can indeed be interpreted as relic gravitons.