3.2. "Exact-Statistical" Approach

As discussed in Section 3.1, in most cases soon after the photoabsorption an isolated nanoparticle (or large molecule) converts almost all of the initial photoexcitation energy to vibrational energy of the highly vibrationally excited ground electronic state, and hence for both neutrals and ions, IR emission is always the dominant deactivation process. Therefore, it is reasonable to model the stochastic heating of a nanoparticle in terms of pure vibrational transitions.

Ideally, if both the vibrational energy levels and the level-to-level transition probabilities were known, we could (at least in principle) solve for the statistical steady-state populations of the different energy levels of grains illuminated by a known radiation field. However, this level of detailed information is generally unavailable, for even the smallest and simplest PAH molecules.

Draine & Li (2001) developed an "exact-statistical" theory for modeling the photoexcitation and emission processes of nanoparticles. In this theory, the state of the grain is characterized by its vibrational energy E. Since there are too many vibrational energy levels to consider individually, they are grouped into (M + 1) "bins" j = 0,..., M, where the j-th bin is [E_{j, min}, E_{j, max}), with representative energy E_j (E_{j, min} + E_{j, max}) / 2, and width E_j (E_{j, max} - E_{j, min}) (see Fig. 3 for illustration). Let P_j be the probability of finding the grain in bin j. The probability vector P_j evolves according to dP_i / dt = _ji T_ij P_j - _ji T_ji P_i for i = 0, 1,..., M, where the transition matrix element T_ij is the probability per unit time for a grain in bin j to make a transition to one of the levels in bin i. If we define the diagonal elements of T to be T_ii - _ji T_ji, then under the steady state condition (i.e. dP_i / dt = 0 for i = 0, 1,..., M) the state probability evolution equation becomes _j=0^M T_ij P_j = 0 for i = 0,..., M. Combining this with the normalization condition _j=0^M P_j = 1, we obtain a set of M linear equations for the first M elements of P_j: _j=0^M-1 (T_ij - T_iM)P_j = - T_iM for i = 0,..., M - 1, which we solve using the bi-conjugate gradient (BiCG) method. The remaining undetermined element P_M is obtained by P_M = - (T_MM)^-1 _j=0^M-1 T_Mj P_j.

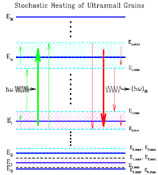Figure 3. Schematic diagram of the vibrational excitation and relaxation processes in nanoparticles (or large molecules). The vibrational energy levels are grouped into (M + 1) "bins" j = 0,..., M, where the j-th bin is [Ej, min, Ej, max), with representative energy Ej (Ej, min + Ej, max) / 2, and width Ej (Ej, max - Ej, min). The ground state is set at E0, min = E0, max = E0 = 0 (see Appendix B of Draine & Li 2001 for the procedure for specifying the bins). The wiggly arrow represents an event of photon absorption (left) or emission (right). The small arrows within the bin u and bin l represent the "intrabin" transitions. With the bin-to-bin transition rates determined, we can solve for the statistical steady-state populations of the different energy states of grains illuminated by a known radiation field, and then calculate the resulting IR emission spectra.

For a given starlight energy density u_E, the state-to-state transition rates T_ji for transitions i j can be determined from photon absorptions and photon emissions. The rate for upward transitions l u is just the absorption rate of photons with such an energy that they excite the grain from bin l just to bin u. If the bin width is sufficiently small (i.e., if max[E_l, E_u] << [E_u - E_l]), the l u excitation rate is simply T_ul C_abs(E) c u_E E_u / (E_u - E_l) for u < M, where C_abs(E) is the grain absorption cross section at wavelength = hc / E (h is the Planck function and c is the speed of light); and T_Ml C_abs(E) c u_E E_M / (E_M - E_l) + _EM-E1 dE C_abs(E) c u_E / (E_M - E_l), where the integral takes energy absorbed in transitions to levels beyond the highest bin and allocates it to the highest bin (M). For the special case of transitions u - 1 u we include "intrabin" absorptions: ₀^E_u-1 dE (1 - E / E_u-1)C_abs(E) c u_E / (E_u - E_u-1). Correction for finite bin width, which is important when the treatment is applied to grains with radii a 50 Å, has been made by Draine & Li (2001) by introducing a G_ul(E) factor (see Eqs.[15-25] of Draine & Li 2001).

The rates for downward transitions u l can be determined from a detailed balance analysis of the Einstein A coefficient. Similarly, if the bin width is sufficiently small, the u l de-excitation rate can be approximated as T_lu (8 / h³ c²) g_l / g_u E_u / (E_u - E_l) E³ × C_abs(E)[1 + (h³ c² / 8 E³) u_E] for l < u -1, where the u_E-containing term is the contribution of stimulated emission, and the degeneracies g_u and g_l are the numbers of energy states in bins u and l, respectively: g_j N(E_{j, max}) - N(E_{j, min}) (dN / dE)_Ej E_j, where (dN / dE)_Ej is the vibrational density of states at internal energy E_j, which corresponds to the number of ways of distributing this energy between different modes of this grain. Again, we refer the reader to Draine & Li (2001) for finite bin width corrections as well as "intrabin" radiation consideration (see Eqs.[29-31] of Draine & Li 2001).

It is seen from the above discussions that we require only C_abs(E), the degeneracies g_j, and the starlight spectrum u_E to completely determine the transition matrix T_ij. A molecule containing N_a atoms will have N_m = 3N_a - 6 distinct vibrational modes (plus 3 translational degrees of freedom and 3 rotational degrees of freedom). If the molecule is approximated as a set of N_m harmonic oscillators, and the frequencies of all normal modes of this molecule are known, we can calculate N(E), the number of distinct vibrational states with total vibrational energy less than or equal to E, using the Beyer-Swinehart algorithm (Beyer & Swinehart 1973; Stein & Rabinovitch 1973). So far, the frequencies of these normal modes have been computed only for a small number of PAHs, with some frequencies determined experimentally, but mode spectra are not yet available for most PAHs of interest.

Since exact densities of states are often unknown for interstellar PAHs, the Whitten & Rabinovitch (1963) approximation, a semi-empirical expression, has been extensively used in literature: (E) = (E + E_z)^N_m-1 / [(N_m - 1)! 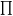_i=1^N_m h_i] where (E) is the density of states (the number of accessible vibrational states per unit energy) at internal energy E, E_z = _i=1^N_m (h_i / 2) is the total zero point energy of the molecule, _i is the vibrational frequency, and 0 < < 1 is an empirical correction factor.

In contrast, the Draine & Li (2001) "exact-statistical" theory does not need this approximation; instead, they calculate the "theoretical" mode spectrum from the Debye model. A PAH molecule containing N_C C atoms and N_H H atoms is treated by Draine & Li (2001) as having 5 different types of vibration: (1) (N_C - 2) out-of-plane C-C modes at _CC,op^-1 = k_{B op} / hc (16.7 µm)^-1 600 cm^-1 given by a two-dimensional Debye model with a Debye temperature _op 950 K, where k_B is the Boltzmann constant, (2) 2(N_C - 2) in-plane C-C modes at _CC,ip^-1 = k_{B ip} / hc (5.7 µm)^-1 1740 cm^-1 given by a two-dimensional Debye model with a Debye temperature _ip 2500 K, (3) N_H out-of-plane C-H bending modes at _CH,op^-1 = (11.3 µm)^-1 886 cm^-1, (4) N_H in-plane C-H bending modes at _CH,ip^-1 = (8.6 µm)^-1 1161 cm^-1, and (5) N_H C-H stretching modes at _CH,str^-1 = (3.3 µm)^-1 3030 cm^-1. The "synthetic" mode spectrum for C₂₄H₁₂ is in excellent agreement with the actual mode spectrum of coronene (see Fig. 1 of Draine & Li 2001). Similarly, a silicate grain containing N_a atoms is treated as having 2 (N_a - 2) vibrational modes distributed according to a two-dimensional Debye model with a Debye temperature = 500 K, and (N_a - 2) modes described by a three-dimensional Debye model with = 1500 K.

From the "synthetic" model mode spectrum we can obtain the vibrational density of states and hence the "degeneracy" g_j, the number of distinct quantum states included in bin j. We note that the densities of states computed for C₂₄H₁₂, using both the actual normal mode spectrum for coronene and the model normal mode spectrum for C₂₄H₁₂ (see Fig. 1 of Draine & Li 2001) are essentially identical for E/hc 300 cm^-1 (see Fig. 4 of Draine & Li 2001). With g_j derived from the model mode spectrum, and the j i (j < i) excitation rates T_ij calculated from a known radiation field with energy density u_E, we can determine the i j (i > j) de-excitation transition rates T_ji. Solving the steady-state state probability evolution equation _ji T_ijP_j = _ji T_ji P_i for i = 0, 1,..., M, we are able to obtain the steady-state energy probability distribution P_j and calculate the resulting IR emission spectrum.

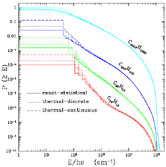Figure 4. The cumulative energy probability distributions for PAHs illuminated by the general ISRF computed using the exact-statistical model, the thermal-discrete model, and the thermal-continuous model. Note that the lowest energy state (E = 0), not shown here, has P(E 0) = 1. Taken from Draine & Li (2001).

In Figure 4 we present the cumulative energy probability distributions for selected PAHs excited by the general solar neighbourhood interstellar starlight radiation field (ISRF) of Mathis, Mezger & Panagia (1983, hereafter MMP) obtained from the "exact-statistical" model. It is seen in Figure 4 that the probability of being in the ground state is very large for small grains: for example, for the MMP radiation field, grains with N_C 4000 spend most of their time at E = 0. The sharp drop at 13.6eV (E / hc 1.1 × 10⁵cm^-1) is due to the radiation field cutoff at 912Å and to the fact that multiphoton events are rare. The resulting IR emission spectra are displayed in Figure 5. The sawtooth features seen at long wavelengths are due to our treatment of transitions from the lower excited energy bins to the ground state and first few excited states (see Section 5.1 and Appendix B of Draine & Li 2001).

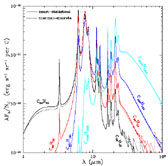Figure 5. IR emissivities (per C atom) for selected ionized PAHs in the general ISRF calculated using the exact-statistical and thermal-discrete models. Taken from Draine & Li (2001).