3.3. "Thermal" Approach

Given (1) the Debye model assumption about the vibrational mode spectrum, (2) the assumption that the absorption cross section C_abs(E) depends only on the photon energy, and (3) the assumption of rapid internal vibrational redistribution, the "statistical" approach described in Section 3.2 is "exact". It is often desirable, however, to use an alternative "thermal" approximation which is less computationally demanding, since the vibrational density of states (E) is a steeply-increasing function of the vibrational energy E (see Fig. 4 of Draine & Li 2001), and for large molecules the number of states is often too large to be tractable even when E is small.

The only difference between the "thermal" approach and the "statistical" approach concerns the calculation of the downward transition rates T_lu which, in contrast to the "exact-statistical" treatment (see Section 3.2), uses the notion of "grain temperature": instead of using degeneracies g_u and g_l, the thermal approach replaces g_l / g_u by (E_l / E_u) {1 / [exp(h / k_B T_u) - 1]}, where T_u is the "temperature" of the upper level u; i.e., the thermal approach assumes that the emission from a molecule with vibrational energy E and N_a atoms can be approximated by the average emission of a system containing 3(N_a - 2) vibrating harmonic oscillators, each with a fundamental frequency _j, connected to a heat bath with temperature T such that the expectation value of the energy of the vibrational system would be E(T) = _j=1^N_m {h_j / [exp (h_j / k_B T) - 1]}. When the number of modes is large, this summation contains many terms. Therefore, we take the Debye model discussed in Section 3.2 for silicate grains and the C-C modes of PAHs to estimate the grain "temperature" associated with internal energy E.

So far, the grains are assumed to undergo "discrete cooling"; i.e., the grains make discrete transitions to energy levels l < u by emission of single photons. There are substantial computational advantages (Guhathakurta & Draine 1989; Draine & Li 2001) if the cooling of the grains is approximated as continuous rather than discrete, so that the only downward transition from a level u is to the adjacent level u - 1 (i.e. T_lu = 0 for u - l > 1). We refer to this as the "thermal continuous" cooling approximation.

In Figure 4 we also plot the cumulative energy probability distributions for selected PAHs excited by the MMP ISRF obtained from the thermal-discrete model, and the thermal-continuous model. It is seen that the energy distributions P(E) found using the thermal-discrete model and the thermal-continuous model are both in good overall agreement with the results of the exact-statistical calculation. The IR emission spectra obtained from the thermal-discrete model, as shown in Figure 5, are almost identical to those of the exact-statistical model. The thermal-continuous cooling model also results in spectra which are very close to those computed using the exact-statistical model (not shown here; see Figs. 14, 15 of Draine & Li 2001).

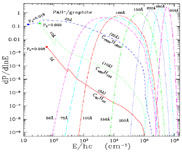Figure 6. The energy probability distribution functions for charged carbonaceous grains (a = 5 Å [C60H20], 10 Å [C480H120], 25 Å [C7200H1800], 50, 75, 100, 150, 200, 250, 300Å) illuminated by the general ISRF. The discontinuity in the 5, 10, and 25 Å curves is due to the change of the estimate for grain vibrational "temperature" at the 20th vibrational mode (see Draine & Li 2001). For 5, 10, and 25Å a dot indicates the first excited state, and P0 is the probability of being in the ground state. Taken from Li & Draine (2001b).

Figure 6 shows the energy probability distribution functions found for PAHs with radii a = 5, 10, 25, 50, 75, 100, 150, 200, 300Å illuminated by the general ISRF. It is seen that very small grains (a 100 Å) have a very broad P(E), and the smallest grains (a < 30 Å) have an appreciable probability P₀ of being found in the vibrational ground state E = 0. As the grain size increases, P(E) becomes narrower, so that it can be approximated by a delta function for a > 250 Å. However, for radii as large as a = 200 Å, grains have energy distribution functions which are broad enough that the emission spectrum deviates noticeably from the emission spectrum for grains at a single "steady-state" temperature T, as shown in Figure 7. For accurate computation of IR emission spectra it is therefore important to properly calculate the energy distribution function P(E), including grain sizes which are large enough that the average thermal energy content exceeds a few eV.

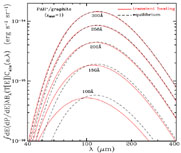Figure 7. Infrared emission spectra for small carbonaceous grains of various sizes heated by the general ISRF, calculated using the full energy distribution function P(E) (solid lines); also shown (broken lines) are spectra computed for grains at the "equilibrium" temperature T. Transient heating effects lead to significantly more short wavelength emission for a 200 Å. Taken from Li & Draine (2001b).