It has been clear since the 1930s that galaxies are not distributed at random in the universe (Hubble 1934). For decades, our understanding of this fact was limited by the lack of a three-dimensional picture, although some impressive progress was made: the dedication of pioneers such as Shane & Wirtanen in compiling galaxy catalogues by eye is humbling to consider. However, studies of the galaxy distribution came of age in the 1980s, via redshift surveys, in which Hubble's v = Hd law is used to turn spectroscopic redshifts into estimates of distance (e.g. Davis & Peebles 1983; de Lapparant, Geller & Huchra 1986; Saunders et al. 1991). We were then able to see clearly (e.g. figure 1) a wealth of large-scale structures of size exceeding 100 Mpc. The existence of these cosmological structures must be telling us something important about the initial conditions of the big bang, and about the physical processes that have operated subsequently. These lectures cover some of what we have learned in this regard.
 |
Figure 1. One of the iconic pictures of the large-scale structure in the galaxy distribution is this slice made from John Huchra's ZCAT compilation of galaxy redshifts, reflecting the state of our knowledge in the mid-1980s. The survey coverage is not quite complete; as well as the holes due to the galactic plane around right ascensions 6h and 19h, the rich clusters are somewhat over-represented with respect to a true random sampling of the galaxy population. Nevertheless, this plot emphasizes nicely both the large-scale features such as the `great wall' on the left, the totally empty void regions, and the radial `fingers of God' caused by virialized motions in the clusters. One of the principal challenges in cosmology is to explain this pattern. |
Throughout, it will be convenient to adopt a notation
in which the density (of mass, light, or any property) is
expressed in terms of a dimensionless density
perturbation 
:
 |
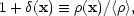(1) |
where
<
> is the
global mean density.
The quantity need not
be small, but writing things
in this form naturally suggests an approach via perturbation
theory in the important linear case where
<< 1.
As we will see, this was a good approximation at early times.
The existence of this field in the universe raises two
questions: what generated it, and how does it evolve?
A popular answer for the first question is inflation, in which quantum
fluctuations are able to seed density fluctuations. So far,
despite some claims, this theory is not tested, and we consider
later some ways in which this might be accomplished.
Mainly, however, we will be concerned here with the question of evolution.