1.2. Relativistic viewpoint and gauge issues

Many of the key aspects of the evolution of structure in the universe can be dealt with via a deceptively simple Newtonian approach, but honesty requires a brief overview of some of the difficult issues that will be evaded by taking this route.

Because relativistic physics equations are written in a covariant form in which all quantities are independent of coordinates, relativity does not distinguish between active changes of coordinate (e.g. a Lorentz boost) or passive changes (a mathematical change of variable, normally termed a gauge transformation). This generality is a problem, since it is not trivial to know which coordinates should be used. To see how the problems arise, ask how tensors of different order change under a gauge transformation x^µ x' ^µ = x^µ + ^µ. Consider first a scalar quantity S (which might be density, temperature etc.). A scalar quantity in relativity is normally taken to be independent of coordinate frame, but this is only for the case of Lorentz transformations, which do not involve a change of the spacetime origin. A gauge transformation therefore not only induces the usual transformation coefficients dx' ^µ / dx, but also involves a translation that relabels spacetime points. We therefore have to deal with S '(x^µ + ^µ) = S(x^µ), so the rule for the gauge transformation of scalars is

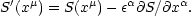(2)

Similar reasoning yields the gauge transformation laws for higher tensors, although we need to account not only for the translation of the origin, but also for the usual effect of the coordinate transformation on the tensor.

Consider applying this to the case of a uniform universe; here only depends on time, so that

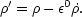(3)

An effective density perturbation is thus produced by a local alteration in the time coordinate: when we look at a universe with a fluctuating density, should we really think of a uniform model in which time is wrinkled? This ambiguity may seem absurd, and in the laboratory it could be resolved empirically by constructing the coordinate system directly - in principle by using light signals. This shows that the cosmological horizon plays an important role in this topic: perturbations with wavelength ct inhabit a regime in which gauge ambiguities can be resolved directly via common sense. The real difficulties lie in the super-horizon modes with ct. However, at least within inflationary models, these difficulties can be overcome. According to inflation, perturbations on scales greater than the horizon were originally generated via quantum fluctuations on small scales within the horizon of a nearly de Sitter exponential expansion. There is thus no problem in understanding how the initial density field is described, since the simplest coordinate system can once again be constructed directly.

The most direct way of solving these difficulties is to construct perturbation variables that are explicitly independent of gauge. Comprehensive technical discussions of this method are given by Bardeen (1980), Kodama & Sasaki (1984), Mukhanov, Feldman & Brandenberger (1992). The starting point for a discussion of metric perturbations is to devise a notation that will classify the possible perturbations. Since the metric is symmetric, there are 10 independent degrees of freedom in g^µ; a convenient scheme that captures these possibilities is to write the cosmological metric as

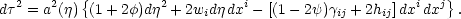(4)

In this equation, is conformal time, and _ij is the comoving spatial part of the Robertson-Walker metric.

The total number of degrees of freedom here is apparently 2 (scalar fields and ) + 3 (3-vector field w) + 6 (symmetric 3-tensor h_ij) = 11. To get the right number, the tensor h_ij is required to be traceless: ^ij h_ij = 0. The perturbations can be split into three classes: scalar perturbations, which are described by scalar functions of spacetime coordinate, and which correspond to the growing density perturbations studied above; vector perturbations, which correspond to vorticity perturbations, and tensor perturbations, which correspond to gravitational waves. Here, we shall concentrate mainly on scalar perturbations. Since vectors and tensors can be generated from derivatives of a scalar function, the most general scalar perturbation actually makes contributions to all the g_µ components in the above expansion:

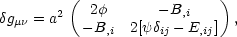(5)

where four scalar functions , , E and B are involved. It turns out that this situation can be simplified by defining variables that are unchanged by a gauge transformation:

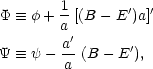(6)

where primes denote derivatives with respect to conformal time.

These gauge-invariant `potentials' have a fairly direct physical interpretation, since they are closely related to the Newtonian potential. The easiest way to evaluate the gauge-invariant fields is to make a specific gauge choice and work with the longitudinal gauge in which E and B vanish, so that = and = . A second key result is that inserting the longitudinal metric into the Einstein equations shows that and are identical in the case of fluid-like perturbations where off-diagonal elements of the energy-momentum tensor vanish. In this case, the longitudinal gauge becomes identical to the Newtonian gauge, in which perturbations are described by a single scalar field, which is the gravitational potential. The conclusion is thus that the gravitational potential can for many purposes give an effectively gauge-invariant measure of cosmological perturbations, and this provides a sounder justification for the Newtonian approach that we now adopt.