


The equations of motion are nonlinear, and we have only solved them in the limit of linear perturbations. We now discuss evolution beyond the linear regime, first for a few special density models, and then considering full numerical solution of the equations of motion.
3.1. The Zeldovich approximation
Zeldovich (1970) invented a kinematical approach to the formation of structure. In this method, we work out the initial displacement of particles and assume that they continue to move in this initial direction. Thus, we write for the proper coordinate of a given particle
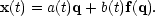 |
(55) |
This looks like Hubble expansion with some
perturbation, which will become negligible as
t  0. The coordinates
q are therefore equal to the usual
comoving coordinates at t = 0, and b(t) is a function
that scales the time-independent displacement field f(q).
In fluid-mechanical terminology, x is said to be the Eulerian
position, and q the Lagrangian position.
0. The coordinates
q are therefore equal to the usual
comoving coordinates at t = 0, and b(t) is a function
that scales the time-independent displacement field f(q).
In fluid-mechanical terminology, x is said to be the Eulerian
position, and q the Lagrangian position.
To get the Eulerian density, we need the Jacobian
of the transformation between x and q,
in which frame  is constant. This strain tensor is symmetric, provided
we assume that the density perturbation originated from a
growing mode. The displacement field is then irrotational, so that
we can write it in terms of a potential
is constant. This strain tensor is symmetric, provided
we assume that the density perturbation originated from a
growing mode. The displacement field is then irrotational, so that
we can write it in terms of a potential
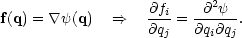 |
(56) |
The strain tensor is thus characterized by its three eigenvalues, and the density becomes infinite when the most negative eigenvalue reaches -1.
If we linearize the density relation, then the relation to density perturbations is
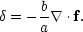 |
(57) |
This is first-order Lagrangian perturbation theory, in contrast to the
earlier approach, which carried out perturbation theory in
Eulerian space (higher-order Lagrangian theory is discussed by
Bouchet et al. 1995).
When the density fluctuations are small, a first-order treatment from
either point of view should give the same result. Since the
linearized density relation is
 = - (b /
a)
= - (b /
a) . f , we can tell immediately that
[b(t) / a(t)] = D(t), where
D(t) is the linear density growth law.
Without doing any more work, we therefore know that the first-order
form of Lagrangian perturbations must be
. f , we can tell immediately that
[b(t) / a(t)] = D(t), where
D(t) is the linear density growth law.
Without doing any more work, we therefore know that the first-order
form of Lagrangian perturbations must be
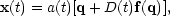 |
(58) |
so that b(t) = a(t)D(t). The advantage of the Zeldovich approximation is that it normally breaks down later than Eulerian linear theory - i.e. first-order Lagrangian perturbation theory can give results comparable in accuracy to Eulerian theory with higher-order terms included. This method is therefore commonly used to set up quasi-linear initial conditions for N-body simulations, as discussed below. The same arguments that we used earlier in discussing peculiar velocities show that the growing-mode comoving displacement field f is parallel to k for a given Fourier mode, so that
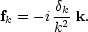 |
(59) |
Given the desired linear density mode amplitudes, the corresponding displacement field can then be constructed.