3.2. The spherical model

An overdense sphere is a very useful nonlinear model, as it behaves in exactly the same way as a closed sub-universe. The density perturbation need not be a uniform sphere: any spherically symmetric perturbation will clearly evolve at a given radius in the same way as a uniform sphere containing the same amount of mass. In what follows, therefore, density refers to the mean density inside a given sphere. The equations of motion are the same as for the scale factor, and we can therefore write down the cycloid solution immediately. For a matter-dominated universe, the relation between the proper radius of the sphere and time is

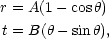(60)

and A³ = GMB², just from 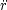= - GM / r². Expanding these relations up to order ⁵ gives r(t) for small t:

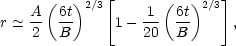(61)

and we can identify the density perturbation within the sphere:

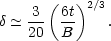(62)

This all agrees with what we knew already: at early times the sphere expands with the a t^2/3 Hubble flow and density perturbations grow proportional to a.

We can now see how linear theory breaks down as the perturbation evolves. There are three interesting epochs in the final stages of its development, which we can read directly from the above solutions. Here, to keep things simple, we compare only with linear theory for an = 1 background.

1. Turnround. The sphere breaks away from the general expansion and reaches a maximum radius at = , t = B. At this point, the true density enhancement with respect to the background is just [A(6t / B)^2/3 / 2]³ / r³ = 9² / 16 5.55. By comparison, extrapolation of linear t^2/3 theory predicts _lin = (3/20)(6)^2/3 1.06.
2. Collapse. If only gravity operates, then the sphere will collapse to a singularity at = 2. This occurs when _lin = (3/20)(12)^2/3 1.69.
3. Virialization. Clearly, collapse will never occur in practice; dissipative physics will eventually intervene and convert the kinetic energy of collapse into random motions. How dense will the resulting body be? Consider the time at which the sphere has collapsed by a factor 2 from maximum expansion. At this point, it has kinetic energy K related to potential energy V by V = - 2K. This is the condition for equilibrium, according to the virial theorem. For this reason, many workers take this epoch as indicating the sort of density contrast to be expected as the endpoint of gravitational collapse. This occurs at = 3/2, and the corresponding density enhancement is (9 + 6)² / 8 147, with _lin 1.58. Some authors prefer to assume that this virialized size is eventually achieved only at collapse, in which case the contrast becomes (6)² / 2 178.

These calculations are the basis for a common `rule of thumb', whereby one assumes that linear theory applies until _lin is equal to some _c a little greater than unity, at which point virialization is deemed to have occurred. Although the above only applies for = 1, analogous results can be worked out from the full _lin(z, ) and t(z, ) relations; _lin 1 is a good criterion for collapse for any value of likely to be of practical relevance. The full density contrast at virialization may be approximated by

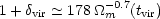(63)

(although open models show a slightly stronger dependence on _m than flat -dominated models; Eke et al. 1996). The faster expansion of low-density universes means that, by the time a perturbation has turned round and collapsed to its final radius, a larger density contrast has been produced. For real non-spherical systems, it is not clear that this distinction is meaningful, and in practice a density contrast of around 200 is used to define the virial radius that marks the boundary of an object.