Having discussed the main elements of the theory of cosmological
structure formation, we now turn to the statistical
treatment of data - which is how theory and observation will
be confronted. The density perturbation field,
,
inhabits a universe that is isotropic and homogeneous
in its large-scale properties, suggesting that the statistical
properties of
should also be homogeneous.
This statement sounds contradictory, and yet it makes
perfect sense if there exists an ensemble of universes.
The concept of an ensemble is used every time we apply probability
theory to an event such as tossing a coin: we imagine an
infinite sequence of repeated trials, half of which
result in heads, half in tails.
The analogy of coin tossing in cosmology is that the density at a given
point in space will have different values in each member
of the ensemble, with some overall variance
<2>
between members of the ensemble. Statistical homogeneity
of the field then means
that this variance must be independent of position. The actual field found
in a given member of the ensemble is a realization of the
statistical process.
There are two problems with this line of argument:
(i) we have no evidence that the ensemble exists;
(ii) in any case, we only get to observe one realization,
so how is the variance
<2> to
be measured? The first objection applies to coin tossing, and
may be evaded if we understand the physics that
generates the statistical process - we only
need to imagine tossing the coin many times,
and we do not actually need to perform the exercise.
The best that can be done in answering the second
objection is to look at widely separated parts of
space, since the fields
there should be causally unconnected; this is therefore as good as taking
measurements from two different member of the ensemble.
In other words, if we measure the variance
<2>
by averaging over a sufficiently large volume, the results
would be expected to approach the true ensemble variance,
and the averaging operator < ... > is often
used without being specific about which kind of average is intended.
Fields that satisfy this property, whereby
 |
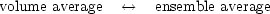(72) |
are termed ergodic. Giving a formal proof of ergodicity for a random process is not always easy (Adler 1981); in cosmology it is perhaps best regarded as a common-sense axiom.