4.1. Fourier analysis of density fluctuations

It is often convenient to consider building up a general field by the superposition of many modes. For a flat comoving geometry, the natural tool for achieving this is via Fourier analysis. For other models, plane waves are not a complete set and one should use instead the eigenfunctions of the wave equation in a curved space. Normally this complication is neglected: even in an open universe, the difference only matters on scales of order the present-day horizon.

How do we make a Fourier expansion of the density field in an infinite universe? If the field were periodic within some box of side L, then we would just have a sum over wave modes:

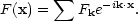(73)

The requirement of periodicity restricts the allowed wavenumbers to harmonic boundary conditions

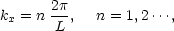(74)

with similar expressions for k_y and k_z. Now, if we let the box become arbitrarily large, then the sum will go over to an integral that incorporates the density of states in k-space, exactly as in statistical mechanics; this is how the general idea of the Fourier transform is derived. The Fourier relations in n dimensions are thus

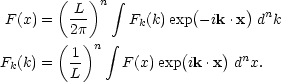(75)

One advantage of this particular Fourier convention is that the definition of convolution involves just a simple volume average, with no gratuitous factors of (2)^-1/2:

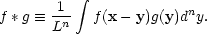(76)

Although one can make all the manipulations on density fields that follow using either the integral or sum formulations, it is usually easier to use the sum. This saves having to introduce -functions in k-space. For example, if we have f = f_kexp(- ikx), the obvious way to extract f_k is via f_k = (1/L) f exp(ikx) dx: because of the harmonic boundary conditions, all oscillatory terms in the sum integrate to zero, leaving only f_k to be integrated from 0 to L. There is less chance of committing errors of factors of 2 in this way than considering f = (L / 2) f_kexp(- ikx) dk and then using exp[i(k - K)x] dx = 2 _D(k - K).

Correlation functions and power spectra     As an immediate example of the Fourier machinery in action, consider the important quantity

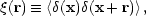(77)

which is the autocorrelation function of the density field - usually referred to simply as the correlation function. The angle brackets indicate an averaging over the normalization volume V. Now express as a sum and note that is real, so that we can replace one of the two 's by its complex conjugate, obtaining

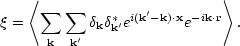(78)

Alternatively, this sum can be obtained without replacing < > by < ^*>, from the relation between modes with opposite wavevectors that holds for any real field: _k(- k) = ^*_k(k). Now, by the periodic boundary conditions, all the cross terms with k' k average to zero. Expressing the remaining sum as an integral, we have

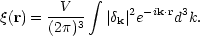(79)

In short, the correlation function is the Fourier transform of the power spectrum. This relation has been obtained by volume averaging, so it applies to the specific mode amplitudes and correlation function measured in any given realization of the density field. Taking ensemble averages of each side, the relation clearly also holds for the ensemble average power and correlations - which are really the quantities that cosmological studies aim to measure. We shall hereafter often use the alternative notation

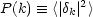(80)

for the ensemble-average power (although this only applies for a Fourier series with discrete modes). The distinction between the ensemble average and the actual power measured in a realization is clarified below in the section on Gaussian fields.

In an isotropic universe, the density perturbation spectrum cannot contain a preferred direction, and so we must have an isotropic power spectrum: <|_k|²(k)> = |_k|²(k). The angular part of the k-space integral can therefore be performed immediately: introduce spherical polars with the polar axis along k, and use the reality of so that e^{-ik . x} cos(kr cos). In three dimensions, this yields

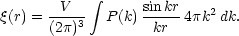(81)

The 2D analogue of this formula is

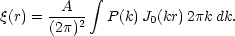(82)

We shall usually express the power spectrum in dimensionless form, as the variance per ln k (²(k) = d<²>/d ln k k³ P[k]):

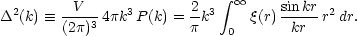(83)

This gives a more easily visualizable meaning to the power spectrum than does the quantity VP(k), which has dimensions of volume: ²(k) = 1 means that there are order-unity density fluctuations from modes in the logarithmic bin around wavenumber k. ²(k) is therefore the natural choice for a Fourier-space counterpart to the dimensionless quantity (r).

Power-law spectra     The above shows that the power spectrum is a central quantity in cosmology, but how can we predict its functional form? For decades, this was thought to be impossible, and so a minimal set of assumptions was investigated. In the absence of a physical theory, we should not assume that the spectrum contains any preferred length scale, otherwise we should then be compelled to explain this feature. Consequently, the spectrum must be a featureless power law:

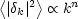(84)

The index n governs the balance between large- and small-scale power. The meaning of different values of n can be seen by imagining the results of filtering the density field by passing over it a box of some characteristic comoving size x and averaging the density over the box. This will filter out waves with k 1/x, leaving a variance <²> ₀^1/x kⁿ 4k² dk x^-(n+3). Hence, in terms of a mass M x³, we have

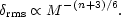(85)

Similarly, a power-law spectrum implies a power-law correlation function. If (r) = (r/r₀)^-, with = n + 3, the corresponding 3D power spectrum is

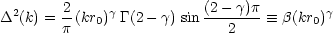(86)

(= 0.903(kr₀)^1.8 if = 1.8). This expression is only valid for n < 0 ( < 3); for larger values of n, must become negative at large r (because P(0) must vanish, implying ₀ (r) r² dr = 0). A cutoff in the spectrum at large k is needed to obtain physically sensible results.

What general constraints can we set on the value of n? Asymptotic homogeneity clearly requires n > - 3. An upper limit of n < 4 comes from an argument due to Zeldovich. Suppose we begin with a totally uniform matter distribution and then group it into discrete chunks as uniformly as possible. It can be shown that conservation of momentum in this process means that we cannot create a power spectrum that goes to zero at small wavelengths more rapidly than _k k². Thus, discreteness of matter produces the minimal spectrum, n = 4. More plausible alternatives lie between these extremes. The value n = 0 corresponds to white noise, the same power at all wavelengths. This is also known as the Poisson power spectrum, because it corresponds to fluctuations between different cells that scale as 1 / M_cell^1/2. A density field created by throwing down a large number of point masses at random would therefore consist of white noise. Particles placed at random within cells, one per cell, create an n = 2 spectrum on large scales.

Practical spectra in cosmology, conversely, have negative effective values of n over a large range of wavenumber. For many years, the data on the galaxy correlation function were consistent with a single power law:

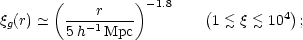(87)

see Peebles (1980), Davis & Peebles (1983). This corresponds to n - 1.2. By contrast with the above examples, large-scale structure is `real', rather than reflecting the low-k Fourier coefficients of some small-scale process.

The Zeldovich spectrum     Most important of all is the scale-invariant spectrum, which corresponds to the value n = 1, i.e. ² k⁴. To see how the name arises, consider a perturbation in the gravitational potential:

(88)

The two powers of k pulled down by ² mean that, if ² k⁴ for the power spectrum of density fluctuations, then ² is a constant. Since potential perturbations govern the flatness of spacetime, this says that the scale-invariant spectrum corresponds to a metric that is a fractal: spacetime has the same degree of `wrinkliness' on each resolution scale. The total curvature fluctuations diverge, but only logarithmically at either extreme of wavelength.

Another way of looking at this spectrum is in terms of perturbation growth balancing the scale dependence of : x^-(n+3)/2. We know that viewed on a given comoving scale will increase with the size of the horizon: r_H². At an arbitrary time, though, the only natural length provided by the universe (in the absence of non-gravitational effects) is the horizon itself:

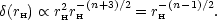(89)

Thus, if n = 1, the growth of both r_H and with time cancels out so that the universe always looks the same when viewed on the scale of the horizon; such a universe is self-similar in the sense of always appearing the same under the magnification of cosmological expansion. This spectrum is often known as the Zeldovich spectrum (sometimes hyphenated with Harrison and Peebles, who invented it independently).

The generic nature of the scale-invariant spectrum makes it difficult to use as a test, since many theories may be expected to have a chance of yielding something like a fractal spacetime. The interesting aspect to focus on is therefore where theory predicts deviations from this rule. Inflation is an interesting case, since the horizon-scale amplitude is expected to change logarithmically with scale in simple models (Hawking 1982):

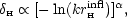(90)

where is a constant of order unity that depends on the inflationary potential ( = 2 for V() = m^{2 2} / 2, for example). Since the proper horizon scale at the end of inflation cannot be infinitely small (a^infl r_H^infl > _Planck), we see that _H should vary by a small but definite amount over the range of scales that can be probed by the CMB and large-scale structure (a change by a factor 1.07 between k = 0.1 h Mpc ^-1 and 10^-3 h Mpc^-1, taking = 1, r_H^infl = _Planck / a^infl and a^infl 2.73 / T_Planck, so that r_H^infl = 10^-3.08m). This is pretty close to scale-invariance, but shows that small amounts of tilt are potentially observable if sufficiently accurate observations can be made.