6.4. Number counts of faint galaxies

The final classical test I will discuss is that of number counts of distant objects - what radio astronomers call the log(N)-log(S) test. Basically one counts the number of galaxies N brighter than a certain flux limit S. If we lived in a static Euclidean universe, then the number of galaxies out to distance R would be N R³ but the flux is related to R as S R^-2. This implies that N S^-3/2 or log(N) = -3/2 log(S) + const = 0.6m + const where m is the magnitude corresponding to the flux S.

But we do not live in a static Euclidean universe; we live in an evolving universe with a non-Euclidean geometry where the differential number counts probe dV(z), the comoving volume as a function of redshift. In Fig. 9 we see log(dV/dz) as a function of redshift for three different (_tot = 1) cosmological models: the matter dominated Universe, the cosmological constant dominated Universe, and the concordance model. For small z, dV/dz increases as z² for all models as would be expected in a Euclidean Universe, but by redshift one, the models are obviously diverging, with the models dominated by a cosmological constant having a larger comoving incremental volume. Therefore if we can observe faint galaxies extending out to a redshift of one or two, we might expect number counts to provide a cosmological probe.

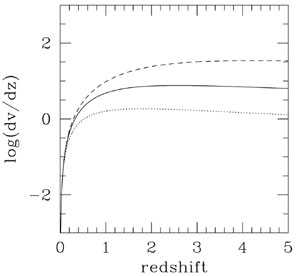Figure 9. The log of the incremental volume per incremental redshift (in units of the Hubble volume) as a function of redshift for the three flat cosmological models.

There is a long history of counting objects as a function of flux or redshift. Although cosmological conclusions have been drawn (see, e.g. [53]), the overall consensus is that this is not a very good test because the galaxy population evolves strongly with redshift. Galaxies evolve because stars evolve. In the past, the stellar populations were younger and contained relatively more massive, luminous stars. Therefore we expect galaxies to be more luminous at higher redshift. It is also possible that the density of galaxies evolves because of merging, as would be consistent with the preferred model of hierarchical structure formation in the Universe.

The distribution of galaxies by redshift can be used, to some extent, to break this degeneracy between evolution and cosmology. If we can measure the redshifts of galaxies with infrared magnitudes between 23 and 26, for example, that distribution will be skewed toward higher redshift if there is more luminosity evolution.

I have recently reconsidered the number counts of the faint galaxies in the Hubble Deep Fields, north and south [55, 56]. These are two separate small patches of empty sky observed with the Hubble Space Telescope down to a very low flux limit - about m_I = 30 (the I band is a far red filter centered around 8000 angstroms). The differential number counts are shown by the solid round points in Fig. 10 where ground based number counts at fainter magnitudes are also shown by the starred points.

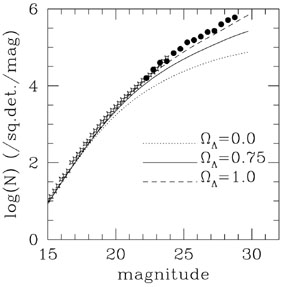Figure 10. The solid points are the faint galaxy number counts from the Hubble Deep Fields (north and south [55, 56]) and the star shaped points are the number counts from ground based data. The curves are the no-evolution predictions from three flat cosmological models.

For this same sample of galaxies, there are also estimates of the redshifts based upon the galaxy colors - so called photometric redshifts [57]. In order to calculate the expected number counts and redshift distribution one must have some idea of the form of the luminosity function - the distribution of galaxies by redshift. Here, like everyone else, I have have assumed that this form is given by the Schechter function [58]:

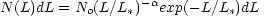(6.6)

which is characterized by three parameters: , a power law at low luminosities, L_* a break-point above which the number of galaxies rapidly decreases, and N_o a normalization. I take this form because the overall galaxy distribution by luminosity at low redshifts is well fit by such a law [59], so I am assuming that at least the form of the luminosity function does not evolve with redshift.

But when I consider faint galaxies at high redshift in a particular band I have to be careful to apply the K-correction mentioned above; that is, I must correct the observed flux in that band to the rest frame. Making this correction [60], but assuming no luminosity or density evolution, I find the differential number counts appropriate to our three flat cosmological models shown by the indicated curves in Fig. 10. We see that the predicted number counts all fall short of the observed counts, but that the cosmological constant dominated model comes closest to matching the observations. However, the distribution by redshift of HDF galaxies between I-band magnitudes of 22 and 26 is shown in Fig. 11 (this is obviously the cumulative distribution). Here we see that all three models seriously fail to match the observed distribution, in the sense that the predicted mean redshift is much too small.

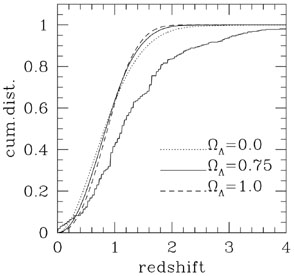Figure 11. The cumulative redshift distribution for galaxies between apparent I-band magnitudes of 23 and 26 (photometric redshifts from [57]). The curves are the predicted no-evolution distributions for the three cosmological models.

This problem could obviously be solved by evolution. If galaxies are brighter in the past, as expected, then we would expect to shift this distribution toward higher redshifts. One can conceive of very complicated evolution schemes, involving initial bursts of star formation with or without continuing star formation, but it would seem desirable to keep the model as simple as possible; let's take a "minimalist" model for galaxy evolution. A simple one parameter scheme with the luminosity brightening proportional to the look-back time squared, i.e., every galaxy brightens as

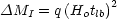(6.7)

where q is the free parameter, can give a reasonable match to evolution models for galaxies [60]. (we also assume that all galaxies are the same- they are not divided into separate morphological classes). I choose the value of q such that the predicted redshift distribution most closely matches the observed distribution for all three models, and the results are shown in Fig. 12.

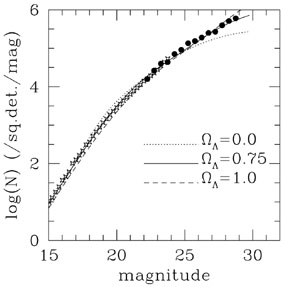Figure 12. As in Fig. 10 above the observed galaxy number counts and the predictions for the cosmological models with luminosity evolution sufficient to explain the number counts.

For these same evolutionary models, that is, with evolution sufficient to match the number counts, the predicted redshift distributions are shown in Fig. 13. Here we see that the model dominated by a cosmological constant predicts too many low redshift galaxies, the matter dominated model predicts too few, and the model that works perfectly is very close to the concordance model! Preforming this operation for a number of flat models with variable , I find that 0.59 < < 0.71 to 90% confidence.

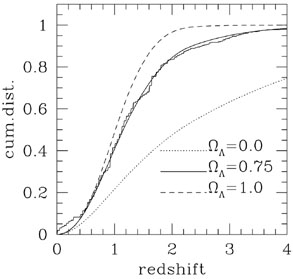Figure 13. The cumulative redshift distribution for galaxies between apparent i-band magnitudes of 22 and 26 (photometric redshifts from [57]). The curves are the predicted distributions for the three cosmological models with evolution sufficient to explain the number counts.