3.5. Dark Energy, or Worse?

If general relativity is correct, cosmic acceleration implies there must be a dark energy density which diminishes relatively slowly as the universe expands. This can be seen directly from the Friedmann equation (17), which implies

(77)

From this relation, it is clear that the only way to get acceleration ( increasing) in an expanding universe is if falls off more slowly than a^-2; neither matter (_M a^-3) nor radiation (_R a^-4) will do the trick. Vacuum energy is, of course, strictly constant; but the data are consistent with smoothly-distributed sources of dark energy that vary slowly with time.

There are good reasons to consider dynamical dark energy as an alternative to an honest cosmological constant. First, a dynamical energy density can be evolving slowly to zero, allowing for a solution to the cosmological constant problem which makes the ultimate vacuum energy vanish exactly. Second, it poses an interesting and challenging observational problem to study the evolution of the dark energy, from which we might learn something about the underlying physical mechanism. Perhaps most intriguingly, allowing the dark energy to evolve opens the possibility of finding a dynamical solution to the coincidence problem, if the dynamics are such as to trigger a recent takeover by the dark energy (independently of, or at least for a wide range of, the parameters in the theory). To date this hope has not quite been met, but dynamical mechanisms at least allow for the possibility (unlike a true cosmological constant).

The simplest possibility along these lines involves the same kind of source typically invoked in models of inflation in the very early universe: a scalar field rolling slowly in a potential, sometimes known as "quintessence" [92, 93, 94, 95, 96, 97]. The energy density of a scalar field is a sum of kinetic, gradient, and potential energies,

(78)

For a homogeneous field ( 0), the equation of motion in an expanding universe is

(79)

If the slope of the potential V is quite flat, we will have solutions for which is nearly constant throughout space and only evolving very gradually with time; the energy density in such a configuration is

(80)

Thus, a slowly-rolling scalar field is an appropriate candidate for dark energy.

However, introducing dynamics opens up the possibility of introducing new problems, the form and severity of which will depend on the specific kind of model being considered. Most quintessence models feature scalar fields with masses of order the current Hubble scale,

(81)

(Fields with larger masses would typically have already rolled to the minimum of their potentials.) In quantum field theory, light scalar fields are unnatural; renormalization effects tend to drive scalar masses up to the scale of new physics. The well-known hierarchy problem of particle physics amounts to asking why the Higgs mass, thought to be of order 10¹¹eV, should be so much smaller than the grand unification/Planck scale, 10²⁵ - 10²⁷ eV. Masses of 10^-33 eV are correspondingly harder to understand. On top of that, light scalar fields give rise to long-range forces and time-dependent coupling constants that should be observable even if couplings to ordinary matter are suppressed by the Planck scale [98, 99]; we therefore need to invoke additional fine-tunings to explain why the quintessence field has not already been experimentally detected.

Nevertheless, these apparent fine-tunings might be worth the price, if we were somehow able to explain the coincidence problem. To date, many investigations have considered scalar fields with potentials that asymptote gradually to zero, of the form e^1/ or 1 / . These can have cosmologically interesting properties, including "tracking" behavior that makes the current energy density largely independent of the initial conditions [100]. They do not, however, provide a solution to the coincidence problem, as the era in which the scalar field begins to dominate is still set by finely-tuned parameters in the theory. One way to address the coincidence problem is to take advantage of the fact that matter/radiation equality was a relatively recent occurrence (at least on a logarithmic scale); if a scalar field has dynamics which are sensitive to the difference between matter- and radiation-dominated universes, we might hope that its energy density becomes constant only after matter/radiation equality. An approach which takes this route is k-essence [101], which modifies the form of the kinetic energy for the scalar field. Instead of a conventional kinetic energy K = 1/2 ()², in k-essence we posit a form

(82)

where f and g are functions specified by the model. For certain choices of these functions, the k-essence field naturally tracks the evolution of the total radiation energy density during radiation domination, but switches to being almost constant once matter begins to dominate. Unfortunately, it seems necessary to choose a finely-tuned kinetic term to get the desired behavior [102].

An alternative possibility is that there is nothing special about the present era; rather, acceleration is just something that happens from time to time. This can be accomplished by oscillating dark energy [103]. In these models the potential takes the form of a decaying exponential (which by itself would give scaling behavior, so that the dark energy remained proportional to the background density) with small perturbations superimposed:

(83)

On average, the dark energy in such a model will track that of the dominant matter/radiation component; however, there will be gradual oscillations from a negligible density to a dominant density and back, on a timescale set by the Hubble parameter, leading to occasional periods of acceleration. Unfortunately, in neither the k-essence models nor the oscillating models do we have a compelling particle-physics motivation for the chosen dynamics, and in both cases the behavior still depends sensitively on the precise form of parameters and interactions chosen. Nevertheless, these theories stand as interesting attempts to address the coincidence problem by dynamical means.

One of the interesting features of dynamical dark energy is that it is experimentally testable. In principle, different dark energy models can yield different cosmic histories, and, in particular, a different value for the equation of state parameter, both today and its redshift-dependence. Since the CMB strongly constrains the total density to be near the critical value, it is sensible to assume a perfectly flat universe and determine constraints on the matter density and dark energy equation of state; see figure (3.8) for some recent limits.

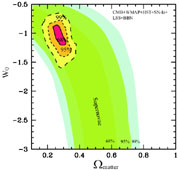Figure 3.8. Constraints on the dark-energy equation-of-state parameter, as a function of M, assuming a flat universe. These limits are derived from studies of supernovae, CMB anisotropies, measurements of the Hubble constant, large-scale structure, and primordial nucleosynthesis. From  [104].

As can be seen in (3.8), one possibility that is consistent with the data is that w < - 1. Such a possibility violates the dominant energy condition, but possible models have been proposed  [105]. However, such models run into serious problems when one takes them seriously as a particle physics theory  [106, 107]. Even if one restricts one's attention to more conventional matter sources, making dark energy compatible with sensible particle physics has proven tremendously difficult.

Given the challenge of this problem, it is worthwhile considering the possibility that cosmic acceleration is not due to some kind of stuff, but rather arises from new gravitational physics. there are a number of different approaches to this [108, 109, 110, 111, 112, 113] and we will not review them all here. Instead we will provide an example drawn from our own proposal [112].

As a first attempt, consider the simplest correction to the Einstein-Hilbert action,

(84)

Here µ is a new parameter with units of [mass] and _M is the Lagrangian density for matter.

The fourth-order equations arising from this action are complicated and it is difficult to extract details about cosmological evolution from them. It is therefore convenient to transform from the frame used in 84, which we call the matter frame, to the Einstein frame, where the gravitational Lagrangian takes the Einstein-Hilbert form and the additional degrees of freedom (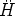 and 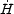) are represented by a fictitious scalar field . The details of this can be found in  [112]. Here we just state that, performing a simultaneous redefinition of the time coordinate, in terms of the new metric 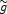_µ, our theory is that of a scalar field (x^µ) minimally coupled to Einstein gravity, and non-minimally coupled to matter, with potential

(85)

Now let us first focus on vacuum cosmological solutions. The beginning of the Universe corresponds to R and 0. The initial conditions we must specify are the initial values of and ', denoted as _i and '_i. For simplicity we take _i << M_p. There are then three qualitatively distinct outcomes, depending on the value of '_i.

1. Eternal de Sitter. There is a critical value of '_i '_C for which just reaches the maximum of the potential V() and comes to rest. In this case the Universe asymptotically evolves to a de Sitter solution. This solution requires tuning and is unstable, since any perturbation will induce the field to roll away from the maximum of its potential.

2. Power-Law Acceleration. For '_i > '_C, the field overshoots the maximum of V() and the Universe evolves to late-time power-law inflation, with observational consequences similar to dark energy with equation-of-state parameter w_DE = -2/3.

3. Future Singularity. For '_i < '_C, does not reach the maximum of its potential and rolls back down to = 0. This yields a future curvature singularity.

In the more interesting case in which the Universe contains matter, it is possible to show that the three possible cosmic futures identified in the vacuum case remain in the presence of matter.

By choosing µ ~ 10^-33 eV, the corrections to the standard cosmology only become important at the present epoch, making this theory a candidate to explain the observed acceleration of the Universe without recourse to dark energy. Since we have no particular reason for this choice, such a tuning appears no more attractive than the traditional choice of the cosmological constant.

Clearly our choice of correction to the gravitational action can be generalized. Terms of the form - µ²⁽ⁿ⁺¹⁾ / Rⁿ, with n > 1, lead to similar late-time self acceleration, with behavior similar to a dark energy component with equation of state parameter

(86)

Clearly therefore, such modifications can easily accommodate current observational bounds [104, 73] on the equation of state parameter -1.45 < w_DE < - 0.74 (95% confidence level). In the asymptotic regime n = 1 is ruled out at this level, while n 2 is allowed; even n = 1 is permitted if we are near the top of the potential.

Finally, any modification of the Einstein-Hilbert action must, of course, be consistent with the classic solar system tests of gravity theory, as well as numerous other astrophysical dynamical tests. We have chosen the coupling constant µ to be very small, but we have also introduced a new light degree of freedom. Chiba [114] has pointed out that the model with n = 1 is equivalent to Brans-Dicke theory with = 0 in the approximation where the potential was neglected, and would therefore be inconsistent with experiment. It is not yet clear whether including the potential, or considering extensions of the original model, could alter this conclusion.