


In the first lecture we described the kinematics and dynamics of homogeneous and isotropic cosmologies in general relativity, while in the second we discussed the situation in our current universe. In this lecture we wind the clock back, using what we know of the laws of physics and the universe today to infer conditions in the early universe. Early times were characterized by very high temperatures and densities, with many particle species kept in (approximate) thermal equilibrium by rapid interactions. We will therefore have to move beyond a simple description of non-interacting "matter" and "radiation," and discuss how thermodynamics works in an expanding universe.
In the first lecture we discussed how to describe matter as a perfect fluid, described by an energy-momentum tensor
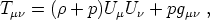 |
(87) |
where Uµ is the fluid four-velocity,
 is the energy
density in the rest frame of the fluid and p is the pressure in that
same frame. The energy-momentum tensor is covariantly conserved,
is the energy
density in the rest frame of the fluid and p is the pressure in that
same frame. The energy-momentum tensor is covariantly conserved,
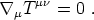 |
(88) |
In a more complete description, a fluid will be characterized by quantities in addition to the energy density and pressure. Many fluids have a conserved quantity associated with them and so we will also introduce a number flux density Nµ, which is also conserved
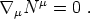 |
(89) |
For non-tachyonic matter Nµ is a timelike 4-vector and therefore we may decompose it as
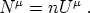 |
(90) |
We can also introduce an entropy flux density Sµ. This quantity is not conserved, but rather obeys a covariant version of the second law of thermodynamics
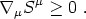 |
(91) |
Not all phenomena are successfully described in terms of such a local entropy vector (e.g., black holes); fortunately, it suffices for a wide variety of fluids relevant to cosmology.
The conservation law for the energy-momentum tensor yields, most importantly, equation (25), which can be thought of as the first law of thermodynamics
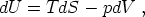 |
(92) |
with dS = 0.
It is useful to resolve Sµ into components parallel and perpendicular to the fluid 4-velocity
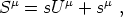 |
(93) |
where sµ Uµ = 0. The scalar s is the rest-frame entropy density which, up to an additive constant (that we can consistently set to zero), can be written as
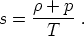 |
(94) |
In addition to all these quantities, we must specify an equation of state, and we typically do this in such a way as to treat n and s as independent variables.