4.6. Finite Temperature Phase Transitions

We have hinted at the need to go beyond perfect fluid sources for the Einstein equations if we are to unravel some of the mysteries left by the standard cosmology. Given our modern understanding of particle physics, it is natural to consider using field theory to model matter at early times in the universe. The effect of cosmic expansion and the associated thermodynamics yield some fascinating phenomena when combined with such a field theory approach. One significant example is provided by finite temperature phase transitions.

Rather than performing a detailed calculation in finite-temperature field theory, we will illustrate this with a rough argument. Consider a theory of a single real scalar field at zero temperature, interacting with a second real scalar field . The Lagrangian density is

(129)

with potential

(130)

where µ is a parameter with dimensions of mass and and g are dimensionless coupling constants.

Now, consider what the effective theory for looks like if we assume that is in thermal equilibrium. In this case, we may replace by the temperature T to obtain a Lagrangian for only, with finite temperature effective potential given by

(131)

This simple example demonstrates a very significant result. At zero temperature, all your particle physics intuition tells you correctly that the theory is spontaneously broken, in this case the global 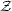₂ symmetry of the Lagrangian is broken by the ground state value <> 0 (we shall see more of this soon). However, at temperatures above the critical temperature T_c given by

(132)

the full 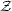₂ symmetry of the Lagrangian is respected by the finite temperature ground state, which is now at <> = 0. This behavior is know as finite temperature symmetry restoration, and its inverse, occurring as the universe cools, is called finite temperature spontaneous symmetry breaking.

Zero temperature unification and symmetry breaking are fundamental features of modern particle physics models. For particle physicists this amounts to the statement that the chosen vacuum state of a gauge field theory is one which does not respect the underlying symmetry group of the Lagrangian.

The melding of ideas from particle physics and cosmology described above leads us to speculate that matter in the early universe was described by a unified gauge field theory based on a simple continuous Lie group, G. As a result of the extreme temperatures of the early universe, the vacuum state of the theory respected the full symmetry of the Lagrangian. As the universe cooled, we hypothesize that the gauge theory underwent a series of spontaneous symmetry breakings (SSB) until matter was finally described by the unbroken gauge groups of QCD and QED. Schematically the symmetry breaking can be represented by

(133)

The group G is known as the grand unified gauge group and the initial breaking G H and is expected to take place at 10¹⁶ GeV, as we discuss below.

Let us briefly set up the mathematical description of SSB which will be useful later when we discuss topological properties of the theory.

Consider a gauge field theory described by a continuous group G. Denote the vacuum state of the theory by | 0>. Then, given g(x) 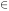G, the state g(x)| 0> is also a vacuum. Suppose all vacuum states are of the form g| 0> but that the state | 0> is invariant only under a subgroup H 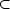G. Then the symmetry of the theory is said to have been spontaneously broken from G to H. 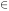Let us define two vacuum states | 0>_A and | 0>_B to represent the same state under the broken group if g| 0>_A = | 0>_B for some g G. We write | 0>_A ~ | 0>_B and the distinguishable vacua of the theory are equivalence classes under ~ and are the cosets of H in G. Then the vacuum manifold, the space of all accessible vacua of the theory, is the coset space

(134)

Given that we believe the universe evolved through a sequence of such symmetry breakings, there are many questions we can ask about the cosmological implications of the scheme and many ways in which we can constrain and utilize the possible breaking patterns.