


4.7. Topological Defects
In a quantum field theory, small oscillations around the vacuum
appear as particles. If the space of possible vacuum states is
topologically nontrivial, however, there arises the possibility of
another kind of solitonic object: a topological defect.
Consider a field theory described by a continuous symmetry group
G which is spontaneously broken to a subgroup
H 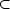 G. Recall that the space of
all accessible vacua of the theory, the vacuum manifold, is
defined to be the space of cosets of H in G;
G. Recall that the space of
all accessible vacua of the theory, the vacuum manifold, is
defined to be the space of cosets of H in G;

 G / H.
Whether the theory admits topological defects depends on whether
the vacuum manifold has nontrivial homotopy groups. A homotopy
group consists of equivalence classes of maps of spheres (with fixed
base point) into the manifold, where two maps are equivalent if they
can be smoothly deformed into each other. The homotopy groups
defined in terms of n-spheres are denoted
G / H.
Whether the theory admits topological defects depends on whether
the vacuum manifold has nontrivial homotopy groups. A homotopy
group consists of equivalence classes of maps of spheres (with fixed
base point) into the manifold, where two maps are equivalent if they
can be smoothly deformed into each other. The homotopy groups
defined in terms of n-spheres are denoted
 n.
n.
In general, a field theory with vacuum manifold
 possesses a topological defect of some type if
possesses a topological defect of some type if
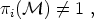 |
(135) |
for some i = 0, 1,.... In particular, we can have a set of defects, as listed in table 3. In order to get an intuitive picture of the meaning of these topological criteria let us consider the first two.
| Homotopy Constraint | Topological Defect |
 0( 0( ) )
 1 1 |
Domain Wall |
 2( 2( ) )
 1 1 |
Cosmic String |
 2( 2( ) )
 1 1 |
Monopole |
 3( 3( ) )
 1 1 |
Texture |
If  0(
0( )
)
 1, the manifold
1, the manifold
 is
disconnected. (A zero-sphere is the set of two points a fixed distance
from the origin in R1. The set of topologically equivalent
maps with fixed base point from such such a sphere into a manifold is
simply the set of disconnected pieces into which the manifold falls.)
Let's assume for simplicity that the vacuum manifold consists
of just two disconnected components
is
disconnected. (A zero-sphere is the set of two points a fixed distance
from the origin in R1. The set of topologically equivalent
maps with fixed base point from such such a sphere into a manifold is
simply the set of disconnected pieces into which the manifold falls.)
Let's assume for simplicity that the vacuum manifold consists
of just two disconnected components
 1 and
1 and
 2 and restrict
ourselves to one spatial dimension. Then, if we apply boundary
conditions that the vacuum at
-
2 and restrict
ourselves to one spatial dimension. Then, if we apply boundary
conditions that the vacuum at
-  lies in
lies in
 1 and that at
+
1 and that at
+  lies in
lies in
 2, by continuity
there must be a point somewhere where the
order parameter does not lie in the vacuum manifold as the field
interpolates between the two vacua. The region in which the field is
out of the vacuum is known as a domain wall.
2, by continuity
there must be a point somewhere where the
order parameter does not lie in the vacuum manifold as the field
interpolates between the two vacua. The region in which the field is
out of the vacuum is known as a domain wall.
Similarly, suppose
 2(
2( )
)
 1. This implies that the
vacuum manifold is not simply-connected: there are
non-contractible loops in the manifold. The order parameter for such a
situation may be considered complex and if, when traveling around a
closed curve in space, the phase of the order parameter changes by a
non-zero multiple of 2
1. This implies that the
vacuum manifold is not simply-connected: there are
non-contractible loops in the manifold. The order parameter for such a
situation may be considered complex and if, when traveling around a
closed curve in space, the phase of the order parameter changes by a
non-zero multiple of 2 , by
continuity there is a point
within the curve where the field is out of the vacuum
manifold. Continuity in the direction perpendicular to the plane of
the curve implies that there exists a line of such points. This is an
example of a cosmic string or line defect. Since we shall mostly
concentrate on these defects let us now give a detailed analysis of
the simplest example, the Nielsen-Olesen vortex in the Abelian
Higgs model.
, by
continuity there is a point
within the curve where the field is out of the vacuum
manifold. Continuity in the direction perpendicular to the plane of
the curve implies that there exists a line of such points. This is an
example of a cosmic string or line defect. Since we shall mostly
concentrate on these defects let us now give a detailed analysis of
the simplest example, the Nielsen-Olesen vortex in the Abelian
Higgs model.
Consider a complex scalar field theory based on the Abelian gauge group U(1). The Lagrangian density for this model is
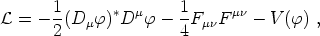 |
(136) |
where
 (x)
is the complex scalar field, the covariant derivative,
Dµ, and field strength tensor
Fµ
(x)
is the complex scalar field, the covariant derivative,
Dµ, and field strength tensor
Fµ are
defined in terms of the Abelian gauge field Aµ as
are
defined in terms of the Abelian gauge field Aµ as
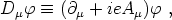 |
(137) |
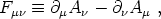 |
(138) |
and the symmetry breaking (or "Mexican hat") potential is
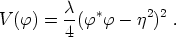 |
(139) |
Here e is the gauge coupling constant and
 is a parameter
that represents the scale of the symmetry breaking. In preparation for our
discussion of the more general cosmological situation, let us note
that at high temperatures the Lagrangian contains
temperature-dependent corrections given by
is a parameter
that represents the scale of the symmetry breaking. In preparation for our
discussion of the more general cosmological situation, let us note
that at high temperatures the Lagrangian contains
temperature-dependent corrections given by
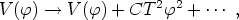 |
(140) |
where C is a constant. For T > Tc, where Tc is defined by
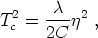 |
(141) |
we see that
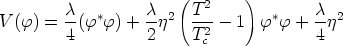 |
(142) |
is minimized by
< > =
0. However, for T < Tc, minimizing the
above expression with respect to
> =
0. However, for T < Tc, minimizing the
above expression with respect to
 yields a
minimum at
yields a
minimum at
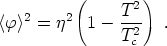 |
(143) |
Thus, for T > Tc the full symmetry group
G = U(1) is restored and the vacuum expectation value of the
 -field is
zero. As the system cools, there is a
phase transition at the critical temperature Tc and
the vacuum symmetry is spontaneously broken, in this case entirely:
-field is
zero. As the system cools, there is a
phase transition at the critical temperature Tc and
the vacuum symmetry is spontaneously broken, in this case entirely:
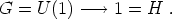 |
(144) |
The vacuum manifold is
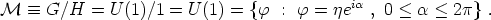 |
(145) |
The group U(1) is topologically a circle, so
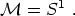 |
(146) |
The set of topologically equivalent ways to map one circle to another circle is given by the integers. (We can wrap it any number of times in either sense.) The first homotopy group is therefore the integers. Calculating homotopy groups in general is difficult, but for S1 all of the other groups are trivial. We therefore have
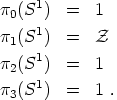 |
(147) (148) (149) (150) |
The Abelian Higgs model therefore allows for cosmic strings.
To see how strings form in this model, consider what happens as T decreases through Tc. The symmetry breaks and the field acquires a VEV given by
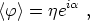 |
(151) |
where  may be chosen
differently in different regions of space, as
implied by causality (we shall discuss this shortly). The requirement
that <
may be chosen
differently in different regions of space, as
implied by causality (we shall discuss this shortly). The requirement
that < > be
single valued implies that around any closed curve in space the change
> be
single valued implies that around any closed curve in space the change

 in
in
 must satisfy
must satisfy
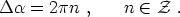 |
(152) |
If for a given loop we have n
 0, then we can see that any
2-surface bounded by the loop must contain a singular point, for if
not then we can continuously contract the loop to a point, implying
that n = 0 which is a contradiction. At this singular point the
phase,
0, then we can see that any
2-surface bounded by the loop must contain a singular point, for if
not then we can continuously contract the loop to a point, implying
that n = 0 which is a contradiction. At this singular point the
phase,  , is undefined and
<
, is undefined and
< > =
0. Further,
<
> =
0. Further,
< >
must be zero all along an infinite or closed
curve, since otherwise we can contract our loop without encountering a
singularity. We identify this infinite or closed curve of false vacuum
points as the core of our string.
We shall restrict our attention to the case where n = 1, since
this is the most likely configuration.
>
must be zero all along an infinite or closed
curve, since otherwise we can contract our loop without encountering a
singularity. We identify this infinite or closed curve of false vacuum
points as the core of our string.
We shall restrict our attention to the case where n = 1, since
this is the most likely configuration.
The first discussion of string solutions to the Abelian Higgs model is
due to Nielsen and Olesen. Assume the string is straight and that
the core is
aligned with the z-axis. In cylindrical polar coordinates,
(r,  ), let
us make the ansatz
), let
us make the ansatz
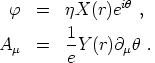 |
(153) |
The Lagrangian then yields the simplified equations of motion
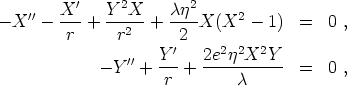 |
(154) |
where a prime denotes differentiation with respect to r. It is not possible to solve these equations analytically, but asymptotically we have
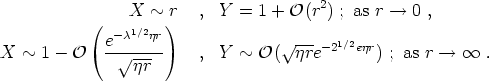 |
(155) |
This solution corresponds to a string
centered on the z-axis, with a central magnetic core of width
~ (e )-1 carrying a total magnetic flux
)-1 carrying a total magnetic flux
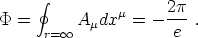 |
(156) |
The core region over which the Higgs fields are appreciably non-zero has
width ~ ( 1/2
1/2
 )-1.
Note that these properties
depend crucially on the fact that we started with a gauged symmetry.
A spontaneously broken global symmetry with nontrivial
)-1.
Note that these properties
depend crucially on the fact that we started with a gauged symmetry.
A spontaneously broken global symmetry with nontrivial
 i(
i( ) would
still produce cosmic strings, but they would be much less localized,
since there would be no gauge fields to cancel the scalar gradients
at large distances.
) would
still produce cosmic strings, but they would be much less localized,
since there would be no gauge fields to cancel the scalar gradients
at large distances.
Strings are characterized by their tension, which is the energy per unit length. For the Nielsen-Olesen solution just discussed, the tension is approximately
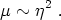 |
(157) |
Thus, the energy of the string is set by the expectation value of the order parameter responsible for the symmetry breaking. This behavior is similarly characteristic of other kinds of topological defects. Again, global defects are quite different; the tension of a global string actually diverges, due to the slow fall-off of the energy density as we move away from the string core. It is often convenient to parameterize the tension by the dimensionless quantity Gµ, so that a Planck-scale string would have Gµ ~ 1.
From the above discussion we can see that cosmology provides us with a unique opportunity to explore the rich and complex structure of particle physics theories. Although the topological solutions discussed above exist in the theory at zero temperature, there is no mechanism within the theory to produce these objects. The topological structures contribute a set of zero measure in the phase space of possible solutions to the theory and hence the probability of production in particle processes is exponentially suppressed. What the cosmological evolution of the vacuum supplies is a concrete causal mechanism for producing these long lived exotic solutions.
At this point it is appropriate to discuss how many of these defects we expect to be produced at a cosmological phase transition. In the cosmological context, the mechanism for the production of defects is known as the Kibble mechanism. The guiding principle here is causality. As the phase transition takes place, the maximum causal distance imposed on the theory by cosmology is simply the Hubble distance - the distance which light can have traveled since the big bang.
As we remarked above, as the temperature of the universe falls well
below the critical temperature of the phase transition,
Tc, the expectation value
of the order parameter takes on a definite value (~
 ei
ei in
the Abelian Higgs model) in each region of space. However, at temperatures
around the critical temperature we expect that thermal fluctuations in
<
in
the Abelian Higgs model) in each region of space. However, at temperatures
around the critical temperature we expect that thermal fluctuations in
< > will
be large so that as the universe cools it will
split into domains with different values of
> will
be large so that as the universe cools it will
split into domains with different values of
 in different domains.
This is the crucial role played by the cosmological evolution.
in different domains.
This is the crucial role played by the cosmological evolution.
The Kibble mechanism provides us with an order of magnitude upper
bound for the size of such a region as the causal horizon size at the time
of the phase transition. The boundaries between the domains will be regions
where the phase of
< >
changes smoothly. If the phase
changes by 2
>
changes smoothly. If the phase
changes by 2 n for some
n
n for some
n  0 when traversing
a loop in space, then
any surface bounded by that loop intersects a cosmic string. These strings
must be horizon-sized or closed loops. Numerical simulations of cosmic
string formation indicate that the initial distribution of strings
consists of 80% horizon-sized and 20% loops by mass. If we
consider the temperature at which there is insufficient thermal energy to
excite a correlation volume back into the unbroken state, the Ginsburg
temperature, TG, then, given the assumption of
thermal equilibrium
above the phase transition, a much improved estimate for the initial
separation of the defects can be derived and is given by
0 when traversing
a loop in space, then
any surface bounded by that loop intersects a cosmic string. These strings
must be horizon-sized or closed loops. Numerical simulations of cosmic
string formation indicate that the initial distribution of strings
consists of 80% horizon-sized and 20% loops by mass. If we
consider the temperature at which there is insufficient thermal energy to
excite a correlation volume back into the unbroken state, the Ginsburg
temperature, TG, then, given the assumption of
thermal equilibrium
above the phase transition, a much improved estimate for the initial
separation of the defects can be derived and is given by
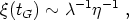 |
where  is the self
coupling of the order parameter. This separation is microscopic.
is the self
coupling of the order parameter. This separation is microscopic.
Interesting bounds on the tension of cosmic strings produced by the Kibble mechanism arise from two sources: perturbations of the CMB, and gravitational waves. Both arise because the motions of heavy strings moving at relativistic velocities lead to time-dependent gravitational fields. The actual values of the bounds are controversial, simply because it is difficult to accurately model the nonlinear evolution of a string network, and the results can be sensitive to what assumptions are made. Nevertheless, the CMB bounds amount roughly to [118, 119, 120, 121]
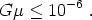 |
(158) |
This corresponds roughly to strings at the GUT scale, 1016 GeV, which is certainly an interesting value. Bounds from gravitational waves come from two different techniques: direct observation, and indirect measurement through accurate pulsar timings. Currently, pulsar timing measurements are more constraining, and give a bound similar to that from the CMB [122]. Unlike the CMB measurements, however, gravitational wave observatories will become dramatically better in the near future, through operations of ground-based observatories such as LIGO as well as satellites such as LISA. These experiments should be able to improve the bounds on Gµ by several orders of magnitude [123].
Now that we have established the criteria necessary for the production of topological defects in spontaneously broken theories, let us apply these conditions to the best understood physical example, the electroweak phase transition. As we remarked earlier, the GWS theory is based on the gauge group SU(2)L × U(1)Y. At the phase transition this breaks to pure electromagnetism, U(1)em. Thus, the vacuum manifold is the space of cosets
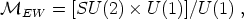 |
(159) |
This looks complicated but in fact this space is topologically equivalent to the three-sphere, S3. The homotopy groups of the three-sphere are
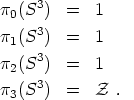 |
(160) (161) (162) (163) |
(Don't be fooled into thinking that all homotopy groups of spheres
vanish except in the dimensionality of the sphere itself; for
example,  3(S2) =
3(S2) = 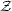 .)
.)
Thus, the electroweak model does not lead to walls, strings, or
monopoles. It does lead to what we called "texture," which
deserves further comment. In a theory where
 3(
3( )
is nontrivial but the other groups vanish,
we can always map three-dimensional space smoothly
into the vacuum manifold; there will not be a defect where the
field climbs out of
)
is nontrivial but the other groups vanish,
we can always map three-dimensional space smoothly
into the vacuum manifold; there will not be a defect where the
field climbs out of  .
However, if we consider field
configurations which approach a unique value at spatial infinity,
they will fall into homotopy classes characterized by elements
of
.
However, if we consider field
configurations which approach a unique value at spatial infinity,
they will fall into homotopy classes characterized by elements
of  3(
3( ); configurations with nonzero
winding will be
textures. If the symmetry is global, such configurations will
necessarily contain gradient energies from the scalar fields. The
energy perturbations caused by global textures were, along with
cosmic strings, formerly popular as a possible origin of structure
formation in the universe
[124,
125];
the predictions of these
theories are inconsistent with the sharp acoustic peaks observed in
the CMB, so such models are no longer considered viable.
); configurations with nonzero
winding will be
textures. If the symmetry is global, such configurations will
necessarily contain gradient energies from the scalar fields. The
energy perturbations caused by global textures were, along with
cosmic strings, formerly popular as a possible origin of structure
formation in the universe
[124,
125];
the predictions of these
theories are inconsistent with the sharp acoustic peaks observed in
the CMB, so such models are no longer considered viable.
In the standard model, however, the broken symmetry is gauged. In this case there is no need for gradient energies, since the gauge field can always be chosen to cancel them; equivalently, "texture" configurations can always be brought to the vacuum by a gauge transformation. However, transitions from one texture configuration to one with a different winding number are gauge invariant. These transitions will play a role in electroweak baryon number violation, discussed in the next section.