


5.2. The Horizon Problem
The horizon problem stems from the existence of particle horizons in FRW cosmologies, as discussed in the first lecture. Horizons exist because there is only a finite amount of time since the Big Bang singularity, and thus only a finite distance that photons can travel within the age of the universe. Consider a photon moving along a radial trajectory in a flat universe (the generalization to non-flat universes is straightforward). In a flat universe, we can normalize the scale factor to
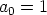 |
(175) |
without loss of generality. A radial null path obeys
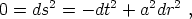 |
(176) |
so the comoving (coordinate) distance traveled by such a photon between times t1 and t2 is
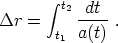 |
(177) |
To get the physical distance as it would be measured by an observer at any time t, simply multiply by a(t). For simplicity let's imagine we are in a matter-dominated universe, for which
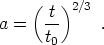 |
(178) |
The Hubble parameter is therefore given by
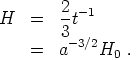 |
(179) |
Then the photon travels a comoving distance
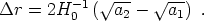 |
(180) |
The comoving horizon size when a = a* is the distance a photon travels since the Big Bang,
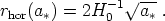 |
(181) |
The physical horizon size, as measured on the spatial hypersurface at a*, is therefore simply
 |
(182) |
Indeed, for any nearly-flat universe containing a mixture of matter and radiation, at any one epoch we will have
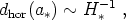 |
(183) |
where H*-1 is the Hubble distance at that particular epoch. This approximate equality leads to a strong temptation to use the terms "horizon distance" and "Hubble distance" interchangeably; this temptation should be resisted, since inflation can render the former much larger than the latter, as we will soon demonstrate.
The horizon
problem is simply the fact that the CMB is isotropic to a high
degree of precision, even though widely separated points on the
last scattering surface are completely outside each others'
horizons. When we look at the CMB we were observing the universe
at a scale factor
aCMB  1/1200; meanwhile, the
comoving distance between a point on the CMB and an observer on Earth is
1/1200; meanwhile, the
comoving distance between a point on the CMB and an observer on Earth is
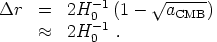 |
(184) |
However, the comoving horizon distance for such a point is
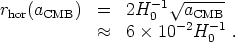 |
(185) |
Hence, if we observe two widely-separated parts of the CMB, they will have non-overlapping horizons; distinct patches of the CMB sky were causally disconnected at recombination. Nevertheless, they are observed to be at the same temperature to high precision. The question then is, how did they know ahead of time to coordinate their evolution in the right way, even though they were never in causal contact? We must somehow modify the causal structure of the conventional FRW cosmology.