


In our previous lectures we have described what is known as the standard cosmology. This framework is a towering achievement, describing to great accuracy the physical processes leading to the present day universe. However, there remain outstanding issues in cosmology. Many of these come under the heading of initial condition problems and require a more complete description of the sources of energy density in the universe. The most severe of these problems eventually led to a radical new picture of the physics of the early universe - cosmological inflation [163, 164, 165], which is the subject of this lecture.
We will begin by describing some of the problems of the standard cosmology.
The Friedmann equation may be written as
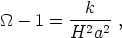 |
(172) |
where for brevity we are now writing
 instead of
instead of
 total.
Differentiating this with respect to the scale factor, this implies
total.
Differentiating this with respect to the scale factor, this implies
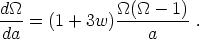 |
(173) |
This equation is easily solved, but its most general properties are all that we shall need and they are qualitatively different depending on the sign of 1 + 3w. There are three fixed points of this differential equation, as given in table 4.
| Fixed Point | 1 + 3w > 0 | 1 + 3w < 0 |
 = 0
= 0 |
attractor | repeller |
 = 1
= 1 |
repeller | attractor |
 = =
 |
attractor | repeller |
Observationally we know that

 1 today - i.e.,
we are
very close to the repeller of this differential equation for a universe
dominated by ordinary matter and radiation (w > - 1/3). Even if we
only took account of the luminous matter in the universe, we would
clearly live in a universe that was far from the attractor points of
the equation. It is already quite puzzling that the universe has not
reached one of its attractor points, given that the universe has
evolved for such a long time. However, we may be more quantitative
about this. If the only matter in the universe is radiation and dust,
then in order to have
1 today - i.e.,
we are
very close to the repeller of this differential equation for a universe
dominated by ordinary matter and radiation (w > - 1/3). Even if we
only took account of the luminous matter in the universe, we would
clearly live in a universe that was far from the attractor points of
the equation. It is already quite puzzling that the universe has not
reached one of its attractor points, given that the universe has
evolved for such a long time. However, we may be more quantitative
about this. If the only matter in the universe is radiation and dust,
then in order to have
 in the range
observed today requires (conservatively)
in the range
observed today requires (conservatively)
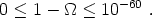 |
(174) |
This remarkable degree of fine tuning is the flatness problem. Within the context of the standard cosmology there is no known explanation of this fine-tuning.