5. THEORY: "UNIVERSAL" (NFW) HALOS VS. ISOTHERMAL HALOS

High-resolution CDM simulations have established the existence of a "universal" density profile for dark matter halos which results from generic dissipationless collapse (e.g., [5], [6], [7], [70], [71], [72], [73], [74], [75]). This density profile fits objects that span roughly 9 orders of magnitude in mass (ranging from the masses of globular star clusters to the masses of large galaxy clusters) and applies to physical scales that are less than the "virial" radius, r₂₀₀. Conventionally, r₂₀₀ is defined to be the radius at which the spherically-averaged mass density reaches 200 times the critical mass density (e.g., [5], [6], [7]).

Navarro, Frenk & White [5], [6], [7] showed that the universal density profile for dark matter halos was fitted well by a function of the form

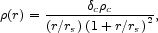(11)

and halos having such a density profile are generally referred to as "NFW" halos. Here _c = (3 H² (z)) / (8 G) is the critical density of the universe at the redshift, z, of the halo, H(z) is Hubble's parameter at that same redshift, and G is Newton's constant. The scale radius r_s r₂₀₀ / c is a characteristic radius at which the density profile agrees with the isothermal profile (i.e., (r) r^-2), c here is a dimensionless number known as the concentration parameter, and

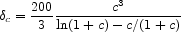(12)

is a characteristic overdensity for the halo.

Formally, the above fitting function for the radial density profiles of CDM halos converges to a steep, cuspy profile: (r) r^-1. The NFW fitting formula, however, was never intended to be extrapolated to very small radii (i.e., radii smaller than the practical resolution limits of the simulations) and much fuss has been made over whether observed galaxies actually show such cuspy inner density profiles (e.g., [76], [77], [78], [79], [80], [81], [82], [83]). More recent numerical work has shown that the density profiles of CDM halos do not, in fact, converge to a well-defined asymptotic inner slope (e.g., [84], [85] [86], [87]), and it has become increasingly clear that fair and direct comparisons of simulated galaxies with observed galaxies on very small physical scales is an extremely challenging thing to do (e.g., [88], [89]).

Weak lensing and satellite dynamics do not have the ability to provide any information whatsoever on the cuspiness (or lack thereof) in the central regions of galaxies. Instead, both are governed by the large-scale properties of the halos (i.e., the regime in which the NFW profile is known to be an excellent description of the density profiles of CDM halos) and, at least in principle, both have the potential to discriminate between NFW halos and simpler singular isothermal sphere halos.

The radial density profile of a singular isothermal sphere halo is given by

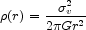(13)

(e.g., [90]), where _v is the velocity dispersion. The isothermal sphere is characterized by the single parameter _v, which is constant as a function of radius. A key prediction for NFW halos, however, is that the radial velocity dispersion will have a strong dependence upon the radius and this, of course, is inconsistent with the constant value of the velocity dispersion that characterizes singular isothermal spheres. Specifically, on sufficiently small scales _r(r) should increase with radius, and on large scales _r(r) should decrease with radius. Hoeft, Mücket & Gottlöber [91] have shown that the radial velocity dispersion of NFW halos can be fitted by a function of the gravitational potential, (r), of the form:

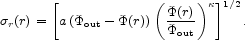(14)

Note that _r(r) above is not the "line of sight" velocity dispersion, since r is a true 3-dimensional radius in eqn. (14). The parameters a and have values of a = 0.29 ± 0.04 and = 0.41 ± 0.03, and _out is the outer potential of the halo. Therefore, we expect the dynamics within an NFW halo to differ fundamentally from the dynamics within an isothermal sphere halo.

In the case of weak lensing, NFW halos give rise to a distortion in the images of distant galaxies that differs somewhat from the distortion that would be yielded by an isothermal sphere halo (e.g., [92], [93]). The radial dependence of the shear for the isothermal sphere is given by:

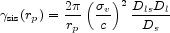(15)

(e.g., [8]). Here c is the velocity of light and D_s, D_l, and D_ls are again angular diameter distances. In the case of NFW halos, the radial dependence of the shear is given by:

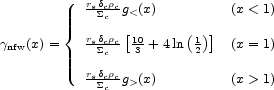(16)

where x r_p/r_s, _c is the critical mass density for gravitational lensing given by eqn. (10), and the functions g_{< , >}(x) are explicitly independent of the cosmology:

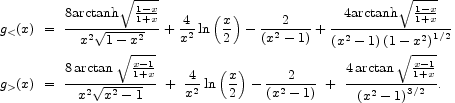(17) (18)

(e.g., [92], [93]).

In the following sections I summarize the most recent attempts to study the dark matter halos of field galaxies through satellite dynamics and weak lensing, including attempts to distinguish between isothermal and NFW potentials on the basis of the velocity dispersion profile and on the weak lensing shear.