The recession factor reduces the rate at which the quanta reach the observer because it dilutes the stream of quanta. The effect is quite simple, and may be described in the following way. Suppose that, in one second of time, a stationary nebula radiates a certain number of quanta n in the direction of the, observer. Since all of the quanta travel with the velocity of light, c miles per second, the first of the quanta to leave the nebula had travelled forward the distance c = 186, 000 miles, when the last of the n quanta leaves the nebula. Thus the n quanta which leave the nebula during one second are scattered uniformly over a path whose length is c.
Now suppose that the nebula is receding from the observer with a velocity of v miles per second. It still radiates the same number of quanta in one second of time, namely n, but during the interval between the emission of the first and the last of these quanta the first quantum has travelled forward the distance c while the nebula has receded the distance v. Thus the n quanta from the receding nebula are distributed over the path c + v, while the same number of quanta from the stationary nebula are distributed over the path c. Evidently, the recession has increased the separation between successive quanta by the factor (c + v) / c = 1 + v / c. The dilution of the stream of quanta necessarily reduces their rate of arrival and, consequently, the apparent luminosity of the nebula. The recession factor 1 + v/c must be applied to a receding nebula, in addition to the energy factor; the observer receives fewer quanta and each of the quanta has lost energy.
In practice, the expression 1 + v / c is generally
replaced by
1 + d
/
, because the use of
the factor implies
an expanding universe, and current theories of such a
universe regard the second expression as the proper
formulation. This procedure is followed in the present discussion.
The recession effect, unlike the energy effect, is not
selective; it is not distorted by the atmosphere, the
telescope, or the photographic film. Consequently, the
recession factor, in its simple form
1 + d /
, may be
applied to apparent luminosities on any system, photographic as well as
bolometric. The fractional reduction
in luminosity is merely the fractional red-shift. In
technical terms apparent magnitudes are increased by the increment
 |
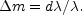The effect of recession is quite negligible for ordinary velocities (or red-shifts) ; for instance, a velocity of 1,860 miles per second (red-shift = 0.01) reduces the apparent luminosity by only 1 per cent. But at great distances, where red-shifts are large, the effects are measurable quantities. For the largest shifts recorded with the spectrograph the reduction is about 14 per cent.; at the limit of the deepest accurate survey, the estimated reduction is about 23 per cent.
It is evident that critical tests of the interpretation of red-shifts as velocity-shifts could be readily made, provided we had reliable distance-criteria which were independent of apparent luminosity. But in the absence of such criteria we must return to the method of parallel hypotheses, and examine the general features of the observable region on the basis of alternative scales of distance.