


The Alternative Laws of Red-Shifts
(a) Red-Shifts not interpreted as Velocity-Shifts
Let us start with the precise formulation of the law of red-shifts. The best data for the purpose are those found in the great clusters of nebulae, for nine or ten of which reliable red-shifts and distances have been derived from the brighter members. The distances range from about 7 million to 240 million light-years, the latter being the greatest reliable distance that has been assigned to an individual object. If peculiarities in the behaviour of red-shifts can be detected at the present time, they will be found in this group of data.
The observational data are quite simple; they consist merely of measured red-shifts and of measured luminosities, corrected for energy-effects. The luminosities indicate the distances, which, of course, are expressed on two scales according to whether or not the recession factors are introduced. Except for the choice of scales, the relative distances are reliable.
Now let us adopt the first alternative and assume that red-shifts are not velocity-shifts, that the universe is not rapidly expanding. In this case the red-shifts are strictly proportional to the distances, over the entire range of the data. Within the very small uncertainties of the measures the law of red-shifts is strictly linear as far out into space as spectra have been recorded. The law is expressed as follows
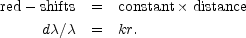 |
The implications of this result are important. If red-shifts are not velocity-shifts, light loses energy strictly in proportion to the distance it travels through space. As light streams in from the remote nebulae in all directions, each million years of the light-paths subtracts the same fraction of energy from the quanta. We may not know how the reduction is accomplished, but we do know that the action is everywhere uniform. Within the small uncertainties of the measures the sample of the universe that can be explored with spectrographs is thoroughly homogeneous.
| Cluster |
d / /
 |
log
d / /
 |
mc* |
| Virgo | 0.0041 | -2.387 | 10.49 |
| Pegasus | 0.0127 | 1.900 | 12.88 |
| Perseus | 0.0174 | 1.759 | 13.48 |
| Coma | 0.0245 | 1.611 | 14.23 |
| U. Ma. I† | 0.0517 | 1.286 | 16.12† |
| Leo | 0.0653 | 1.185 | 16.33 |
| Cor. Bor. | 0.0707 | 1.151 | 16.54 |
| Bootes | 0.1307 | 0.884 | 17.89 |
| U. Ma. II † | 0.1403 | -0.853 | 17.73† |
* mc, is the apparent magnitude of the fifth brightest nebula in the cluster, corrected for local obscuration and for energy-effects of red-shifts. The distance of a cluster is indicated by the relation, log r = 0.2 mc + 4.29 . † The data for the two Ursa Major clusters are the most uncertain of those in the table, because the red-shifts are each derived from a single spectrogram of a single nebula. The data are taken from Contributions of the Mount Wilson Observatory, No. 549; Astrophysical Journal, 84, 270, 1936. |
|||
There are no systematic departures from uniformity whose trends can be pushed out into the universe at large. The homogeneity may extend indefinitely, or trends may exist which only become appreciable beyond the range of the spectrograph; on these questions our knowledge fails and we are reduced to mere speculation. If the explored region is a fair sample, it is relatively insignificant, and it furnishes only negative information concerning a universe that must be vastly greater. This conclusion seems plausible and, in a sense, familiar.
 |
|
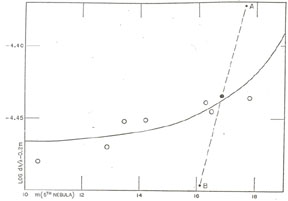
Fig. 1. The Linear Law of Red-Shifts not interpreted as Velocity-Shifts. Each point represents the mean red-shift for a great cluster together with the distance indicator, namely, the apparent magnitude of the fifth brightest nebula, corrected for energy effects of the red-shifts. The data are found in Table 1. The pointsA and B, referring to the two Ursa Major clusters, have small weight, and are combined into the mean point represented by the large black disk. The points define the straight line,
whose slope establishes the linearity of the law of red-shifts out as far as spectra have been recorded. The inclusion of recession factors would displace all the points to the left by amounts which increase from left to right (with increasing m), thus destroying the linearity of the law of red-shifts. The displacements are not conspicuous on the scale of the diagram, and they are shown separately in Fig. 2. |
(b) Red-Shifts interpreted as Velocity-Shifts
But suppose that red-shifts are velocity-shifts, and that the nebulae are receding. Then the law of red-shifts furnishes information, not concerning the contents or properties of internebular space, but concerning the expansion of the universe as a whole. There seems to be no a priori necessity for a linear law of expansion, a strict proportionality between red-shifts and distance. Indeed, the general theory indicates that the law must depart from linearity. If our sample is sufficiently large we may, perhaps, observe the departures and determine their trend. The information would immediately restrict our actual world to a particular family of possible worlds.
With this end in view let us re-examine the data for the great clusters, applying to the luminosities the additional correction for recession. The corresponding distances, of course, are systematically altered but the distortions are not uniform. Distances as previously estimated, without the recession factor, are now shortened, and by percentages which increase with the distance. For instance, the distance to the nearest cluster is reduced by less than one-fifth of 1 per cent., while the distance of the most remote cluster is reduced by about 7 per cent. The red-shifts, however, remain unchanged.
Consequently, the law of red-shifts, which was linear when the recession factor was omitted, cannot be linear when the recession factor is included. We now observe a small but systematic trend away from the linear law. These departures are our first positive clue to the structure of the universe. If the universe is expanding, we know something about how it expands. Our sample is large enough to be significant.
 |
||
Fig. 2. Departures from Linearity in the
Law of Red-Shifts interpreted as Velocity-Shifts.
The points refer to the same clusters as those in
Fig. 1. The red-shifts
are unchanged but the magnitudes have been further corrected by the
recession factors. The vertical scale represents departures from a
linear law of red-shifts. For a linear law,
log d
and the points in the diagram would cluster around a horizontal line.
Actually, the quantities
log d
by which the law of red-shifts is commonly expressed in relativistic cosmology. As in Fig. 1 the two points A and B are combined into the single mean point represented by the large black disk. |
The departures are positive - in other words, the red-shift for a given distance is larger than the linear law would lead us to expect. Moreover, the departures, the differences between the observed law and the linear law, increase with distance at an accelerated rate. The new law may be written by adding a term to the old law; thus
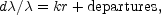 |
where the departures are some function of the distance r. The actual observations, because of the small, residual uncertainties of the measures, might be represented well enough by many different functions of the distance. However, we will follow the custom of relativistic cosmology, and use a power series as a first approximation to the real function. Then the series
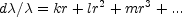 |
represents the non-linear law of red-shifts that follows from the assumption that red-shifts are velocity-shifts.
The first term kr is the linear relation previously derived without the correction for recession. Expressed in terms of velocities the value of k represents a rate of increase of about 100 miles per second per million light-years of distance. Before the new investigations were made, the 'velocity-distance relation', as the law of red-shifts was often called, included this first term alone. The relation was known to be approximately linear and the precision of the data did not justify the addition of the small, higher order terms. The linear term, when followed out into space, suggested that the velocity of light itself would be reached at a distance of about 1,860 million light-years, or less than four times the average distance of the faintest nebulae recorded with the 100-inch reflector.
Moreover, the receding nebulae could be traced backward in time to a very remarkable epoch, about 1,860 million years ago. At that epoch the nebulae would all have been found in our immediate neighbourhood. The present distribution would be reproduced if all the nebulae, being then in a compact cluster, had suddenly started to recede at different velocities. The fastest would now be the most distant, while the slowest would still be in our vicinity. Evidently, the present distances would be proportional to the velocities. The initial instant, the famous t0, is back in time about 1,860 million years. In the favoured, expanding worlds of relativistic cosmology, the period was generally called `the age of the universe', the time-interval since the expansion began.
Efforts were made to crowd a vast multitude of events into the brief span, but serious difficulties were encountered. These difficulties often led to the expectation that, when departures from the approximate linear 'velocity-distance relation' were finally detected, they would prove to be negative. In other words, it was expected, or hoped, that further investigations would show that the expansion began very slowly but continually accelerated until it reached the enormous speed we observe today. Consequently, the true age of the universe would be much greater than that estimated from the provisional linear relation.
Well, we have the first intimation of the nature of the departures - and they are positive. Long ago when the light we now record left the very distant nebulae, the expansion was more rapid than it is today. The time-scale is not lengthened; on the contrary, it is materially shortened. This feature of the expansion is contained in the second term of the power series representing the non-linear law of red-shifts, namely, the term lr2. Actually, the third, and higher, order terms should be included with the second term, but they are presumably so small that they can be neglected in the present discussion. Within the range of existing spectrographs, at any rate, they are smaller than the uncertainties of the measures.
The coefficient l is definitely a positive quantity, and its value is about 2.5 × 10-19 (light-years)-2. Expressed in terms of velocities it corresponds to about one-twentieth of a mile per second at a distance of a million light-years. The term seems insignificant, and certainly it does not become appreciable until great distances are reached. Thereafter, it increases rapidly, for the coefficient is multiplied by the square of the distance. At 100 million light-years the term adds about 500 miles per second to the linear term, and at 500 million light-years about 12,500 miles per second.
The chief significance of the term for cosmological theory lies in the positive sign. The rate of expansion of the universe has been slowing down, at least for the past several hundred million years. The `age of the universe' is considerably shorter than that permitted by the linear law, although the precise, numerical reduction cannot be determined until the third and higher terms of the power series have been evaluated. The maximum permissible span appears to be of the order of 1,500 million years, but the true value might lie anywhere between the maximum and half the maximum. The initial instant, the t0, clearly falls within the life-history of the earth, probably within the history of life on the earth. And, as we look back into time with. our telescopes, we pass in review from a half to a third of the entire period of expansion.