12.5.7. Energy Considerations

The problem of the origin and evolution of extra-galactic radio sources has been a formidable one; in particular the source of energy needed to account for the large power output and the manner in which this energy is converted to relativistic particles and magnetic flux is still a mystery. Assuming only that synchrotron radiation from ultrarelativistic electrons is responsible for the observed radiation, the necessary energy requirements may be estimated in a straight-forward way.

If the relativistic particles have a power law distribution with an index between E₁ and E₂, then for 2, the energy contained in relativistic electrons is

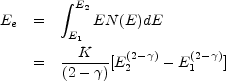(12.26)

The constant K can be evaluated if the distance to the source is known; then the total luminosity L of the source may be estimated by integrating the observed spectrum, giving ( 3)

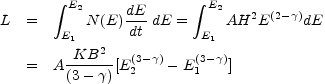(12.27)

or, for = 2.5, H = 100 km/sec/Mpc, and q₀ = + 1,

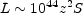(12.28)

where S = flux density at 1 GHz.

Eliminating K we have

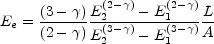(12.29)

Using Equation (12.5) to relate E₂ and E_l to the cut-off frequency, and grouping all the constant terms together,

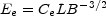(12.30)

The magnetic energy is just

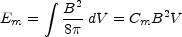(12.31)

The total energy in fields and particles (E_e + E_m) is minimized when

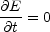(12.32)

or when

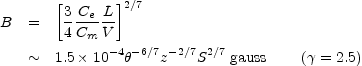(12.33)

The value of B estimated in this way depends almost entirely on the angular size, , and is relatively insensitive to the flux density or distance.

From Equations (12.30), (12.31), and (12.33), if is expressed in arc seconds,

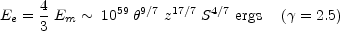(12.34)

That is, the energy is nearly equally distributed between relativistic particles and the magnetic field.

Somewhat surprisingly there is little relation between the minimum energy computed in this way and the total radio luminosity. Typically, the total energy contained in the extended sources estimated is in the range 10⁵⁷ to 10⁶¹ ergs and the magnetic field between 10^-5 and 10^-4 gauss. It is largely because of this apparent very great energy requirement (up to 0.01% of the rest energy of an entire galaxy) that theoretical efforts to explain the origin of radio galaxies have been for the most part unsuccessful.

One interesting result is that if E_e ~ E_m the total energy strongly depends on the size of the source (E r^9/7). This gives the curious situation that the larger sources with low surface brightness and low luminosity, such as Centaurus A, appear to contain almost as much energy as the smaller high surface brightness objects such as Cygnus A. This is not, of course, what would be expected if, as generally assumed, the larger sources were older; this has led to the interesting suggestion that sources may collapse rather than expand. Another way out of this situation which also reduces the energy requirements on the larger sources is that if, as recent observations suggest, sources break up into a number of small components, or if the emission comes from only a thin shell, only a small fraction, , of the projected volume of a source actually has particles and a magnetic field. The minimum total energy is then multiplied by a factor of ^3/7, and the corresponding magnetic field is increased by the factor ^-2/7. Finally, of course, we remark that there is no direct evidence that these minimum energy calculations are at all relevant. The true conditions may show considerable departure from equipartition; however, this greatly amplifies the energy requirements.

For some years it was widely thought that the relativistic electrons were secondary particles produced as the result of collisions between high-energy protons. If the ratio of energy in protons to that in electrons is k, then the minimum total energy is increased by a factor of (1 + k)^4/7 and the magnetic field by (1 + k)^2/7. Estimates of the value of k were about 100, so the energy requirements were about an order of magnitude greater. However, the discovery of rapid time variations in many sources, and its implications for the rapid production of particles, suggests that the secondary production mechanism is probably not relevant, and unnecessarily exaggerates the energy requirements. This elimination of the factor k, and inclusion of the fill-in-factor, , can easily reduce the energy estimates by two or more orders of magnitude.

A characteristic lifetime for radio sources may be estimated from the relation t ~ E / (dE / dt). Lifetimes of radio sources determined in this way are very long. For E ~ 10⁶¹ and (dE / dt) ~ 10⁴⁵ ergs/sec the lifetime is 10⁸ to 10⁹ years. Similar ages are obtained from the fraction (~ 10%) of giant elliptical galaxies that are found to be strong radio sources, and an estimated age of 10¹⁰ years for the age of elliptical galaxies.

Equation (12.15) shows that in a 10^-4 Gauss field, electrons radiating at > 1 GHz are expected to decay in about 10⁶ years. Thus the absence of a spectral cut-off even at 10 GHz suggests a continued or multiple injection of relativistic particles (e.g., van der Laan and Perola, 1969), or a very short lifetime.

For the compact opaque sources magnetic field strength is given directly by the measured peak surface brightness (S_max / ²) the frequency of maximum flux density, _m, and Equation (12.22). For the relatively nearby radio galaxies with small redshifts the magnetic field derived in this way is independent of the redshift, and in any case depends only weakly on the redshift. If the distance is known, then the total energy in the form of relativistic particles, E_p, is given by

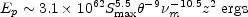(12.35)

and the magnetic energy, _m, by

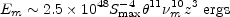(12.36)

while the ratio of the two quantities is given

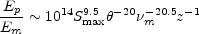(12.37)

In Equations (12.35) to (12.37) is in milliarc seconds, S in f.u., _m, in GHz, H = 100 km/sec/Mpc, and = - 0.75.

Although the energies calculated in this way are very sensitive to the observed size and self-absorption cut-off frequencies, estimates of the energy content can be made at least for those sources where there is accurate data. For the relatively nearby compact radio galaxies, such as NGC 1275, the energy content is ~ 10⁵² ergs. If the compact quasars are at cosmological distances, their energies are considerably greater and are about 10^55±2 ergs.

The energies derived for the compact sources are very much less than the minimum energy of the extended sources, so that a single compact source does not simply evolve by expansion into an extended source. The relation between the compact and extended sources is particularly unclear, since both the luminosity, L, and energy content, E, decrease with expansion. As discussed in Section 12.5.9, L r^-2, and of course E r^-1. Thus, taking 100 arc sec and 0.001 are sec as dimensions of typical extended and compact sources and = - 0.75( = 2.5), upon expansion the energy and luminosity are decreased by a factor of 10⁵ and 10²⁵, respectively, so that even a multiple explosion of compact sources does not appear adequate to explain the extended sources.

It is clear therefore that some continuing energy supply must be available. A possible mechanism for this has been suggested by Rees (1971), who has proposed that the relativistic particles are accelerated by low-frequency electromagnetic waves generated by the release of rotational energy of collapsing stars at the galactic nucleus. The subsequent motion of the particles in the electromagnetic field then produces a "synchro-Compton" radiation, similar in many ways to the usual synchrotron emission of electrons in a magnetic field. One particular attraction for this model is that it avoids the problem of generating a large magnetic flux.