III. SHARPER FOCUS

When a discovery is already done, it usually appears so ev-
ident that one cannot but wonder why nobody hit upon it before.
P.A.M. Dirac 1977

3.1. A feel of group velocity

And yet, though it may be premature to speak of spiral waves
as true modes of oscillation, it seems entirely appropriate to
ask how some postulated spiral wave pattern in a galactic disk
would evolve with time.
Toomre 1969, p.899

The WKBJ-style hot-disk dispersion relation admitted at least two different treatments. Lin and Shu's rested on its `modal' form (). Looking for a particular two-armed spiral wave, they let it rotate with some angular speed <sub>p</sub>, converted it to its pure-note frequency = 2<sub>p</sub>, got it differentially `Doppler-shifted', _* = - 2 (r), found a ratio _* / and, upon substituting it into (), obtained and plotted the ready-to-serve interarm-spacing function (r) and its pitch-angle cousin i(r) = (r) / r.

More in Lindblad's spirit, though equivalent, was the treatment stressing that the dispersion relation specified the reduction of free oscillation frequency to some || due to gravitational star coupling. This provided a deeper look at the so called `dispersion orbits' - ovals composed of many separate test stars at their judiciously phased gyrations about a mean circumferential radius but devoid of self-gravity. Such `orbits' precess at a rate _pr(r) = - / 2, and if general rotation did ensure an approximate radial independence of this combination, that alone would give practical prospects of plaiting the happily co-revolving ovals into a common quasi-steady two-armed pattern. Nature's choice proved slow variability of - / 2, however, as if implying that there might be reason to try the possibility of reducing _pr(r) to a common value by allowing for the as-yet-dormant star coupling. Indeed, that pointed at _pr = - || / 2 = _p = const with its now Lin-Shu tuning formula () for selecting spiral geometries (r), but to make this chance really work, it needed to be demonstrated that the desired tuning of the precession rates could actually be accomplished simultaneously, over a large radial span, and with plausible interarm spacings.

Yet some restrictions were to be placed on these considerations. One was that in a disk of stars the WKBJ waves could not abandon the territory fenced by their related ILR and OLR. But Lin and Shu, who had rightly fixed it in their 1964 patent, found this partial ban to be even a positive factor as they let it favor the prevalence of two-armed spirals, on the simple ground that only those might occupy the entire disk region between the best separable m = 2 Lindblad resonances. Still, for tentative disks reserving local stability there happened to be another type of basic restriction.

Despite several early cautions (Kalnajs 1965, Julian 1967), Lin and Shu kept on exploring their waves for the extra-helpful special case Q = 1.0 only. This persistence seemed to annoy Toomre until late 1967 when he "finally ground out for [him]self what their dispersion relation would imply" at Q > 1 (Toomre). He plotted (k) for different Q's (Fig.8) and found that the case Q = 1.0 was in a sense degenerate: it did let the WKBJ waves reach the corotation circle from both sides, but just a minuscule addition to Q was enough to create their forbidden near-corotation zone that already for as not so very much as Q = 1.2 paralyzed quite a sizable portion of the disk. ⁴⁷

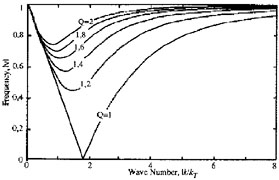Figure 8. The Lin-Shu-Kalnajs dispersion relation. Wavenumbers are in units of kT = 2 / T. (The figure is reproduced from Toomre 1969)

Not even this, however, was the chief restriction to the envisaged frequency-tuning success. "Lin and Shu completely overlooked that in repairing one serious defect they had actually created another: An inevitable price for altering those speeds of precession in a wavelength-dependent manner via the (very sensible) radial forces is a group velocity, likewise directed radially" (Toomre 1977, p.449). Evaluation of this `price' made the point of Toomre's work "Group velocity of spiral waves in galactic disks" (Toomre 1969, hereinafter T69). In his preliminary "Note on group velocity" that in late 1966 was privately circulated at MIT, Toomre had discussed the dispersive properties of the original cold disk by Lin and Shu and called upon extending his discussion to their newer and fairer hot model. <sup>48</sup> But Lin himself "never took it very seriously", and not only because there were "plenty of reasons not to brag about that old note" (Toomre). More generally, at the time he fell into a muse over the role of his introduced `reduction factor', when the group aspect might well appear to him merely as an unnecessary tedious detour in the pursuit of his plain ideas, so that he got no particular intention to `comb' the hairy and transcendental Bessel functions and the like in his dispersion relation for finding out some certain explicit function (k) just to take its trite derivative. ⁴⁹

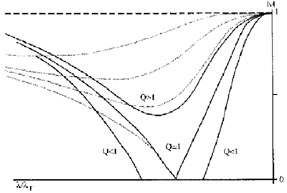Figure 9. The Lin-Shu-Kalnajs dispersion relation in the `modal' form (). Shu's original curves (reproduced from Shu 1968) are given against the exact (lighter) curves

Lin: "The general theory of group velocity is a well-developed and much taught (e.g. in quantum mechanics) classical study valid for any dispersion relationship connecting that wave number with the frequency. Different people will feel differently whether it is even necessary to go beyond taking the derivative and develop it anew for any each specific application. I adopted the empirical approach. [...] That was directly related to the calculation (or derivation) of the dispersion relationship. For this calculation, Frank Shu did his share. The Lin & Shu 1964 paper showed that the crucial step is the calculation of the reduction factor. [...] As I worked out the dispersion relationship, I realized that the present problem is further complicated by the presence of resonances. Thus the hope of success in the calculation of modes depends on a very long-term effort (as it indeed turned out to be the case). Thus our strategy not to pursue the dynamical approach immediately turned out to be the right choice." ⁵⁰ (Lin)

Shu: "I remember Lin telling me that he had group velocity well before the T69 paper on the subject; however, none of us then had any idea (a) what the group velocity carried, and (b) why the concept would be relevant to disturbances with a single value of the wave frequency." (Shu)

Toomre: "The reasons why one does or does not choose to attack some scientific problem from a particular direction are rather `artistic' in nature, and hard to make (or even hope to make) very sound and rational. [...] Surely group velocity may be terribly `obvious' in retrospect to various learned scholars, but I believe it did not seem so to Shu at the time he struggled with his 2^nd-order WKBJ thesis at Harvard." (Toomre)

The main reason why Toomre took to the topic seriously in late 1967 only, about two years after his work with Julian had been completed and the Lin & Shu 1966 paper published, was that in the global-mode context the latter seemed to him to be no more than a trial exploration, and what he judged vitally important and necessary to prove or disprove those authors' `asymptotic' hopes was a full-fledged disk analysis. ⁵¹

"In that climate of opinion it wasn't immediately evident to me, or to anyone else, that one would learn much from the group velocity of those short WKBJ waves that Lin and Shu (1966) were suddenly proposing. Of course I was wrong there, but at least I can boast that by 1969 I myself had repaired that oversight!" (Toomre)

Toomre became the first to take real action on the evident understanding that if indeed a quasi-steady spiral mode can form in a galaxy disk, then it does it via natural wave-packet evolution. And group velocity, he showed, describes at least qualitatively how different kinds of information from the packet are transmitted along the radius, being therefore directly related to the maintenance of all sorts of spiral patterns, even steady ones.

⁴⁷ To be true, Shu was the first to discuss the Q 1 disks publicly, he did it in his thesis (Shu 1968) when attempting to "finish cataloging the nature of the dispersion relation for neutral waves" (S68, p.113). Because this nature "changes somewhat when Q 1", he "briefly summarize[d] [its] salient points" (p.114) using a special plot (Fig.9). For the Q > 1 that summary read: "There is a region about || = 0 for which spatially oscillatory waves cannot propagate. Toomre (private communication) has computed that for values of Q which are moderately greater than unity, the region of inaccessible || can be quite substantial. [...] Such an effect is not too serious since for pattern frequencies of the range to be considered [...] the corresponding annular region where spatially oscillatory waves cannot exist is small in comparison with the range where they can exist. When Q is greater than unity, the reflection, refraction, and tunneling of propagating waves by and through such annular regions become a serious problem for investigation" (p.116). Shu, however, did not explain, nor did he even hint, why he let this serious problem miss the threshold case Q = 1 where his proposed `Mode-A' was so welcome to cross corotation smoothly, i.e. with no reflection, no refraction and no change in the sign of group velocity. Back.

⁴⁸ As defined in the standard d / dk fashion, the `group velocity' of a rotating cold disk grows infinite as one approaches the critical wavelength _T, below which the model gets unstable. Back.

⁴⁹ "Besides, why in fact would anyone want to differentiate the frequency only with respect to the radial wavenumber k instead of also the circumferential wavenumber m, since `everyone knows' that a group velocity is a vector quantity, with components in both directions? This question sounds pretty silly in retrospect, but obstacles like that often seem a lot taller when they are first met." (Toomre) Back.

⁵⁰ In 1968 Lin gave a course at the Brandeis University Summer Institute, with the purpose "to present the modern version of the density wave theory as developed over the past few years by myself and my collaborators Frank H. Shu, Chi Yuan, and William W. Roberts" (Lin & Shu 1971, p.239). Put on paper, that course appeared as Lin & Shu 1971. Speaking there of the spiral interest of prominent astronomers for many years, the authors emphasized that "until recently, however, there has always existed the dilemma of differential rotation", and claimed that "in this article, [they] shall present an essentially stellar dynamical theory for the persistence of the spiral pattern in the presence of differential rotation" (Lin & Shu 1971, p.239, 248). Then - as originally in Lin & Shu 1964 - they "venture[d] to suggest that there are indeed large-scale neutral (or nearly neutral) waves of spiral form for most of the disk galaxies, and formulate[d] [their] ideas in the form of the [QSSS] hypothesis". They pointed out that accepting it and "following the line of reasoning that led to it" one infers, among other things, that in the coordinate system rotating with the pattern "all phenomena are stationary" and "both the stream lines and the magnetic field lines form closed nearly circular loops coinciding with each other" (Lin & Shu 1971, p.248). Then the authors gave a basic presentation of the WKBJ dispersion relation and of the ensuing comparison with observations, and concluded that their spiral theory "needs extension in several directions to complete the theoretical understanding of basic mechanisms and to develop its implications". The directions there envisaged were (1) the "Thickness effect", (2) the "Complete formulation of the theory", (3) the problem of the "Origin of galactic spirals" that "cannot be solved without using the complete formulation mentioned above", and (4) the "Nonlinear theory", becoming important as "one looks beyond the developments of the complete linear theory". In topic (3) the authors enthused on the promising "preliminary indications" and called for "much work [that still] remains to be done", mentioning in a footnote that "Toomre (private communication) has also carried out studies involving the propagation of a group of waves and their initiation by external agents" (Lin & Shu 1971, pp.287-289). Back.

⁵¹ "In essence, I was there just echoing what Agris Kalnajs actually wrote in his not-very-conclusive but nonetheless farsighted concluding chapter on "Instabilities and Spiral Structure" of his 1965 thesis. Yes, it seemed to both him and me at the time - plus probably Hunter, Lynden-Bell, Lebovitz, etc. - that there was a lot of hard but very promising work to be done on the `global' behavior of full-scale disks." (Toomre) Back.