3.2. Group properties of tightly wrapped packets

...a shatteringly destructive article.
Lynden-Bell & Kalnajs 1972, p.1

Various properties of certain types of waves are described in a unified way, regardless of the specific sort of the medium in which they propagate. Such, for instance, are nearly plane - weakly modulated - waves (x, t) = A(x, t) cos[S(x, t)] whose amplitude A(x, t) is much less dependent of its arguments than the phase S(x, t). Their wave vector k = - S and frequency = S / t get connected through a link k / t + = 0 meaning conservation of the wave crests in number, their being neither created nor annihilated. One more link is the common dispersion relation (x, t) = f[k(x, t), (x, t)] (with parametric -dependence reflecting spatial inhomogeneity). Together, these two connections form equations

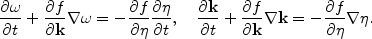(1)

Their characteristic curves coincide with the solution x(t) of the equation

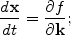(2)

they are understood as rays, in analogy with geometric optics. Determined by the left-hand side of (2), vector c_gr plays as group velocity, with it information on and k is conveyed along the ray. If the medium is in general motion with a speed U(x, t), the waves are carried away. A co-moving observer finds their frequency shifted, = _* + k U (asterisk marking the shifted quantity), and the equations (1), (2) preserving their form. In particular, for the Lin-Shu WKBJ waves they become

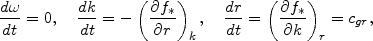(3)

right how Toomre wrote them having k and m as radial and azimuthal wavenumbers, and = _* + m(r).

Equations (3) describe the radial transmission of the signals informing one about invariable wave frequency and knowingly changing wavenumber. Toomre computed them for an easy-to-use but realistic model with Q = const, V = r (r) = const where the rays r(t) just repeat, in relabeled axes, the form of the dispersion curve _*(k). They are followed always in the sense of growing k, because of which leading waves (k < 0) can do nothing but unwind while those trailing (k > 0) wind up more and more. Given by the local `slope' dr / dt, c_gr changes its sign as the ray reflects from the near-corotation barrier, and the Lin-Shu adopted short-wave branch of the solutions has it negative inside corotation, or directed inwards. A value c_gr -10 km/sec that Toomre found for the solar vicinity yields an estimate of few galactic years only for the signal to travel from corotation to the ILR. To an already existing tightly wound trailing pattern, an entire ray family may be compared in its part after the near-corotation turning point, giving exhaustive knowledge on the current and following dynamics of such a wave packet (Fig.10): its information will simply be conveyed inward and gather all at the ILR where the wave group velocity and pitch angle tend to zero.

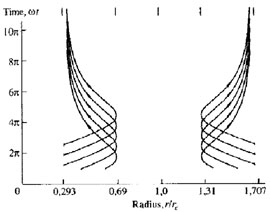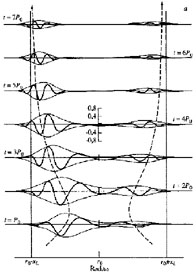
Figure 10. Some m = 2 characteristic curves (rays) for a disk in which Q = 1.2 The x-axis is scaled in corotation radius units. (The figure is reproduced from Toomre 1969)

To illustrate these `information' results, Toomre computed the wave-packet evolution. There he relied on the program that had served him and Julian for local needs of their Cartesian model (JT), because that model luckily revealed an ability to mimic not only the corotation resonance x = 0 but also the Lindblad resonances, since stars placed at and moving along lines x = ± x<sub>L</sub> = ± / 2A k<sub>y</sub> at the expense of shear were ascertained to feel a cos(k<sub>y</sub>y) wave at their natural frequency . <sup>52</sup> Toomre placed a short-term emitter of such waves a little below x = - x<sub>L</sub> - this imitated a bar - and purposely chose rather long-wave situations <sub>y</sub> / <sub>T</sub> 4 where the JT-exploited swing amplifier was all but shut off. His computations showed that the `bar'-induced trailing-wave packet propagates outwards; that its envelope drifts in approximate conformity with the established by the ray methods characteristic curve; that indeed a larger part of energy flow is reflected somewhere near corotation; and that the packet drifts back to x = - x_L where it eventually damps (Fig.11a).

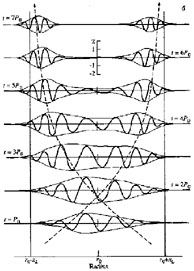Figure 11. A density wave evolving (a) in the Q = 1.2 and (b) Q = 1.0 local models. r0, r0-xL and r0 + xL are the corotation, ILR and OLR radii, xL = T, P0 = 2 / 0. (The figure is reproduced from Toomre 1969)

The wave-packet evolution in the threshold Q = 1.0 disk was of particular interest. While the Lin-Shu theory allowed the tightly wrapped waves to reach and touch the corotation circle, it did not know if they could cross it. And these waves showed they really could: the packet readily invaded all the healthy tissue between the ILR and OLR, and even got amplified to a degree, but then the inevitable group drift constricted it like a sausage at x = 0, squeezed it out of that region and took the forming parts to their LR destinations, as in the common case of Q > 1 (Fig.11b). ⁵³

Now what physically do the waves carry over the star disk and how do they do it? This question was not trivial at the time. Only by the mid-1960s Whitham had worked out a general variational principle for describing a wide class of wave fields with dispersion. For weakly modulated packets it led to the equation

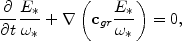(4)

expressing conservation of the wave-action density E_* / _* and its along-ray transmission with group velocity (E_* being the mean volume density of low-amplitude waves, and c_gr E_* - its flow). Toomre conceived that this should be applicable to the Lin-Shu waves as well, ⁵⁴ and felt that the 2^nd-order WKBJ theory, which Shu had already been developing to estimate the rates of change of wave amplitudes with radius, should also yield an accurate radial derivative of E_*. The dE_* / dr that he first inferred from Shu's analyses differed in two small but vital ways from that implied by equation (4). However Toomre suspected that some errors had crept into Shu's work. In due course he located them, and Shu soon concurred (Shu 1970b, c). ⁵⁵ After these small repairs, as Toomre remarked (T69, p.910), Shu's work unwittingly closed the main logical gap of his own paper, and this concluded his expose of the serious strategic error by Lin and Shu - their oversight of the group velocity.

⁵² Of interest is the following record made by Toomre in January 1968. "The linearly shearing, constant surface density model of a star disk that was used by Bill Julian and myself admittedly lacks i) curvature, ii) boundaries, and iii) any gradients of unperturbed quantities such as c_r² or . Nevertheless it can be used in the following manner to illustrate to all desired numerical accuracy not only C.C.'s dispersion relation for tightly wrapped spiral waves, but also the related transient behavior and the transfer of energy. The point is that if one were for some reason to choose any specific circumferential wave number in the JT model, then as Agris correctly pointed out during Frank Shu's thesis exam yesterday, our model, too, would have various Lindblad resonance radii [...and the region between them] will then correspond to what C.C. and Frank call the `principal range'." (Toomre) Back.

⁵³ The question on the preferable sense of spiral winding was not discussed explicitly in T69. Toomre (as well as several others) held that its full solution might be obtained only in the global-wave setting of the spiral problem. At the same time, he was sure that several local findings already gave a sufficient understanding of the trailing-sense benefits. He meant, above all, the delayed character of cooperative star wakes of non-axisymmetric forcing from individual material clumps in a galaxy disk, and the group properties of the Lin-Shu spirals. Indeed, since we do not observe them at the stages of very loose winding and cross orientations, these stages either went already (or were altogether absent) or they still shall have to go. In the first case we have the trailing spirals whose old times are almost unknown to us but whose long-lived future is unambiguously associated with states pretty close to the today's one. In the second case, we would have the leading spirals, huddling up to their ILR and extremely tightly wrapped in order to avoid premature unwinding before too long. Besides, not to forget, the waves of the short-length limit get excited with almost no concern of self-gravity, so that only some `pressure'-force mechanism can generate them. But what might be concretely any such `elastic' mechanism localized in a narrow circumcentral ILR region, and how would it manage to create a practically circular wave running away (c_gr > 0) from a gently sloping (inelastic) `beach' of the ILR instead of rushing on it just like an ocean wave? Only something akin to a Maxwell demon, Toomre guessed, could manufacture such short leading waves.

Yet he mentioned them once in T69 in the positive sense. Speaking in a footnote of plausible variants for either one or both m = 2 Lindblad resonances to be absent from a galaxy disk, he remarked that "in such cases the given wave packet must in some sense be reflected either from the outer edge of the disk or from its center" and that "in the process the character will presumably change from trailing to leading, and the sign of the group velocity should also reverse" (T69, p.909). But, true, at that time Toomre did not think seriously about any such conversion. Back.

⁵⁴ "I was glad enough to brag there that I could also figure out that energy density itself, [... but] I was yet prouder of noticing and pointing out that the main conserved density is not even that energy as such, but instead the action density [...] which Kalnajs in turn soon told me had to be `the excess density of angular momentum associated with the wave'. [...] There was nothing very original about either accomplishment, though of course it could not have been entirely obvious a priori that Whitham's Lagrangian reasoning would apply here as well, with these collisionless stars rather than some more standard fluid." (Toomre) Back.

⁵⁵ (Toomre): "Even in 1967 I was well aware that Frank Shu seemed to be progressing nicely with his thesis, and was still claiming to confirm and to expand upon the `gradient instability' which he and C.C. had announced rather cryptically in Lin & Shu 1966. In detail, I did not pay much attention until he had finished, but then gave his analysis an exceptionally close going-over once he had been awarded his PhD. [...] Amidst his immense and rather impressive 2^nd-order WKBJ calculation I eventually located two small algebraic errors, once I had suspected because his inferred dE/dr did not quite match what I had hoped for in what became eqn (34) of T69. Frank soon agreed, and that was the end of those gradient instabilities!"

(Kalnajs): "As to the famous `gradient instabilities' I went as far as to type up a short paper, dated July 29, 1968. I used my integral equation to show that if you put corotation at the outer edge and made the same sort of tightly wound approximations as Lin and Shu, then there could not be any instabilities. But David Layzer thought that it would be far better if my first publication on density waves made a positive contribution. So this effort remained in a drawer. As it turned out, the 1969 Toomre paper made a positive contribution to the field and at the same time debunked the `gradient instabilities'."

Indeed, in a year Shu found it "apparent that the growth (or decay) of the wave amplitude arises because the disturbance is propagated radially in an inhomogeneous medium and not because the disturbance is inherently overstable" (Shu 1970c, p.110). Back.