


B. The cosmological constant
Special relativity is very successful in laboratory physics. Thus
one might guess any inertial observer would see the same
vacuum. A freely moving inertial observer represents spacetime in
the neighborhood by locally Minkowskian coordinates, with the
metric tensor
 µ
µ given in Eq.
(14). A Lorentz transformation
to an inertial observer with another velocity does not change
this Minkowski form. The same must be true of the stress-energy
tensor of the vacuum, if all observers see the same vacuum,
so it has to be of the form
given in Eq.
(14). A Lorentz transformation
to an inertial observer with another velocity does not change
this Minkowski form. The same must be true of the stress-energy
tensor of the vacuum, if all observers see the same vacuum,
so it has to be of the form
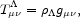 |
(19) |
where

 is
a constant, in a general coordinate labeling. On writing this
contribution to the stress-energy
tensor separately from all the rest, we bring the field
equation (17) to
is
a constant, in a general coordinate labeling. On writing this
contribution to the stress-energy
tensor separately from all the rest, we bring the field
equation (17) to
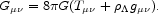 |
(20) |
This is
Einstein's (1917)
revision of the field equation of general relativity, where

 is
proportional to his cosmological constant
is
proportional to his cosmological constant
 ; his reason for
writing down this equation is discussed
in Sec. III.A. In many dark energy
scenarios
; his reason for
writing down this equation is discussed
in Sec. III.A. In many dark energy
scenarios 
 is a slowly varying function of time and its stress-energy
tensor differs slightly from Eq. (19), so the
observed properties of the vacuum do depend on the observer's velocity.
is a slowly varying function of time and its stress-energy
tensor differs slightly from Eq. (19), so the
observed properties of the vacuum do depend on the observer's velocity.
One sees from Eqs. (14), (18), and (19) that the new component in the stress-energy tensor looks like an ideal fluid with negative pressure
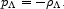 |
(21) |
This fluid picture is of limited use, but the following properties are worth noting. 10
The stress-energy tensor of an ideal fluid with four-velocity
uµ generalizes from Eq. (18) to
Tµ =
(
=
( +
p)uµ
u
+
p)uµ
u -
pgµ
-
pgµ . The
equations of fluid dynamics follow from the vanishing of the
divergence of
Tµ
. The
equations of fluid dynamics follow from the vanishing of the
divergence of
Tµ . Let
us consider the simple case of
locally Minkowskian coordinates, meaning free fall, and a fluid
that is close to homogeneous. By the latter we mean the fluid
velocity
. Let
us consider the simple case of
locally Minkowskian coordinates, meaning free fall, and a fluid
that is close to homogeneous. By the latter we mean the fluid
velocity  --
the space part of the four-velocity uµ -- and the
density fluctuation
--
the space part of the four-velocity uµ -- and the
density fluctuation 
 from
homogeneity may be treated in linear
perturbation theory. Then the equations of energy and momentum
conservation are
from
homogeneity may be treated in linear
perturbation theory. Then the equations of energy and momentum
conservation are
 |
(22) |
where cs2 = dp /
d and
the mean density and pressure are
<
and
the mean density and pressure are
< >
and <p>. These combine to
>
and <p>. These combine to
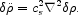 |
(23) |
If cs2 is positive this is a wave equation, and cs is the speed of sound.
The first of Eqs. (22) is the local energy
conservation law, as in Eq. (9). If p =
-  ,
the pdV work cancels the
,
the pdV work cancels the
 dV part:
the work done to increase the volume cancels the effect of the
increased volume. This has to be so for a Lorentz-invariant
stress-energy tensor, of course, where all
inertial observers see the same vacuum. Another way to see this
is to note that the energy flux density in Eqs. (22)
is (<
dV part:
the work done to increase the volume cancels the effect of the
increased volume. This has to be so for a Lorentz-invariant
stress-energy tensor, of course, where all
inertial observers see the same vacuum. Another way to see this
is to note that the energy flux density in Eqs. (22)
is (< > +
<p>)
> +
<p>) .
This vanishes
when p = -
.
This vanishes
when p = -  :
the streaming velocity loses meaning. When
cs2 is negative
Eq. (23) says the fluid is unstable, in general. But when p =
-
:
the streaming velocity loses meaning. When
cs2 is negative
Eq. (23) says the fluid is unstable, in general. But when p =
-  the
vanishing divergence of
Tµ
the
vanishing divergence of
Tµ becomes
the condition seen in Eq. (22) that
becomes
the condition seen in Eq. (22) that
 =
<
=
< > +
> +
 is constant.
is constant.
There are two measures of gravitational interactions with a
fluid: the passive gravitational mass density determines how the
fluid streaming velocity is affected by an applied gravitational
field, and the active gravitational mass density determines the
gravitational field produced by the fluid. When the fluid
velocity is nonrelativistic the expression for the former in
general relativity is
 + p, as
one sees by writing out the covariant divergence of
Tµ
+ p, as
one sees by writing out the covariant divergence of
Tµ .
This vanishes when
p = -
.
This vanishes when
p = -  ,
consistent with the loss of meaning of the streaming velocity.
The latter is
,
consistent with the loss of meaning of the streaming velocity.
The latter is  + 3p, as one sees from Eq. (8). Thus a fluid with
p = -
+ 3p, as one sees from Eq. (8). Thus a fluid with
p = -  /
3, if somehow kept homogeneous and
static, would produce no gravitational field.
11 In the model in
Eqs. (19) and (21) the active gravitational mass density is
negative when
/
3, if somehow kept homogeneous and
static, would produce no gravitational field.
11 In the model in
Eqs. (19) and (21) the active gravitational mass density is
negative when

 is
positive. When this positive
is
positive. When this positive

 dominates the stress-energy tensor
dominates the stress-energy tensor
 is positive: the rate
of expansion of the universe
increases. In the language of Eq. (20), this
cosmic repulsion is a gravitational effect of the negative active
gravitational mass density, not a new force law.
is positive: the rate
of expansion of the universe
increases. In the language of Eq. (20), this
cosmic repulsion is a gravitational effect of the negative active
gravitational mass density, not a new force law.
The homogeneous active mass represented by
 changes the
equation of relative motion of freely moving test particles in
the nonrelativistic limit to
changes the
equation of relative motion of freely moving test particles in
the nonrelativistic limit to
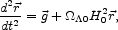 |
(24) |
where 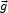 is the relative gravitational acceleration produced by the distribution of
ordinary matter. 12
For an illustration of the size of the last term
consider its effect on our motion in a nearly circular orbit
around the center of the Milky Way galaxy. The Solar System is
moving at speed vc = 220 km s-1 at radius
r = 8 kpc. The ratio of the acceleration
g
is the relative gravitational acceleration produced by the distribution of
ordinary matter. 12
For an illustration of the size of the last term
consider its effect on our motion in a nearly circular orbit
around the center of the Milky Way galaxy. The Solar System is
moving at speed vc = 220 km s-1 at radius
r = 8 kpc. The ratio of the acceleration
g produced by
produced by  to
the total gravitational acceleration g =
vc2 / r is
to
the total gravitational acceleration g =
vc2 / r is
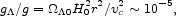 |
(25) |
a small number. Since we are towards the edge of the luminous
part of our galaxy, a search for the effect of
 on the
internal dynamics of galaxies like the Milky Way does not look
promising. The precision of celestial dynamics in the Solar System
is much greater, but the effect of
on the
internal dynamics of galaxies like the Milky Way does not look
promising. The precision of celestial dynamics in the Solar System
is much greater, but the effect of
 is very much smaller;
for the orbit of the Earth,
g
is very much smaller;
for the orbit of the Earth,
g / g ~ 10-22.
/ g ~ 10-22.
One can generalize Eq. (19) to a variable

 ,
by taking
p
,
by taking
p to be negative but different from
-
to be negative but different from
- 
 .
But if the dynamics were that of a fluid, with pressure a function of
.
But if the dynamics were that of a fluid, with pressure a function of

 ,
stability would require cs2 =
dp
,
stability would require cs2 =
dp / d
/ d
 > 0,
from Eq. (23), which seems quite contrived. A viable working
model for a dynamical
> 0,
from Eq. (23), which seems quite contrived. A viable working
model for a dynamical

 is
the dark energy of a scalar field
with self-interaction potential chosen to make the variation of the
field energy acceptably slow, as discussed next.
is
the dark energy of a scalar field
with self-interaction potential chosen to make the variation of the
field energy acceptably slow, as discussed next.
10 These arguments have been familiar, in some circles, for a long time, though in our experience discussed more often in private than the literature. Early statements of elements are in Lemaître (1934) and McCrea (1951); see Kragh (1999, pp. 397-8) for a brief historical account. Back.
11 Lest we contribute to a wrong problem
for the student we note that a fluid with
p = -  /
3 held in a
container would have net positive gravitational mass, from the
pressure in the container walls required for support against the
negative pressure of the contents. We have finessed the walls by
considering a homogeneous situation. We believe
Whittaker (1935)
gives the first derivation of the relativistic active
gravitational mass density. Whittaker also presents an example of
the general proposition that the active gravitational mass of an
isolated stable object is the integral of the time-time part of
the stress-energy tensor in the locally Minkowskian rest frame.
Misner and Putman (1959)
give the general demonstration.
Back.
/
3 held in a
container would have net positive gravitational mass, from the
pressure in the container walls required for support against the
negative pressure of the contents. We have finessed the walls by
considering a homogeneous situation. We believe
Whittaker (1935)
gives the first derivation of the relativistic active
gravitational mass density. Whittaker also presents an example of
the general proposition that the active gravitational mass of an
isolated stable object is the integral of the time-time part of
the stress-energy tensor in the locally Minkowskian rest frame.
Misner and Putman (1959)
give the general demonstration.
Back.
12 This assumes the particles are close enough for application of the ordinary operational definition of proper relative position. The parameters in the last term follow from Eqs. (8) and (21). Back.