


These comments on what people were thinking are gleaned from the literature and supplemented by private discussions and our own recollections. More is required for a satisfactory history of the subject, of course, but we hope we have captured the main themes of the discussion and the way the themes have evolved to the present appreciation of the situation.
Einstein disliked the idea of an island universe in asymptotically flat spacetime, because a particle could leave the island and move arbitrarily far from all the other matter in the universe, yet preserve all its inertial properties, which he considered a violation of Mach's idea of the relativity of inertia. Einstein's (1917) cosmological model accordingly assumes the universe is homogeneous and isotropic, on average, thus removing the possibility of arbitrarily isolated particles. Einstein had no empirical support for this assumption, yet it agrees with modern precision tests. There is no agreement on whether this is more than a lucky guess.
Motivated by the observed low velocities of the then known stars,
Einstein assumed that the large-scale structure of the universe
is static. He introduced the cosmological constant to reconcile
this picture with his general relativity theory. In the notation
of Eq. (12), one sees that a positive value of

 0
can balance the positive values of
0
can balance the positive values of
 M0 and
M0 and
 R0 for
consistency with
R0 for
consistency with
 = 0. The balance is
unstable: a small perturbation
to the mean mass density or the mass distribution causes expansion
or contraction of the whole or parts of the universe. One sees this in
Eq. (24): the mass distribution can be chosen
so the two terms on the right hand side cancel, but the balance
can be upset by redistributing the mass.
13
= 0. The balance is
unstable: a small perturbation
to the mean mass density or the mass distribution causes expansion
or contraction of the whole or parts of the universe. One sees this in
Eq. (24): the mass distribution can be chosen
so the two terms on the right hand side cancel, but the balance
can be upset by redistributing the mass.
13
Einstein did not consider the cosmological constant to be part of the stress-energy term: his form for the field equation (in the streamlined notation of Eq. [17]) is
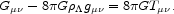 |
(34) |
The left hand side contains the metric tensor and its
derivatives; a new constant of nature,
 , appears
in the addition to Einstein's original field equation.
One can equally well put Einstein's new term on the right hand
side of the equation, as in Eq. (20), and count
, appears
in the addition to Einstein's original field equation.
One can equally well put Einstein's new term on the right hand
side of the equation, as in Eq. (20), and count

 gµ
gµ as
part of the source term in the stress-energy tensor.
The distinction becomes interesting when
as
part of the source term in the stress-energy tensor.
The distinction becomes interesting when

 takes part in the dynamics, and the field equation is properly written
with
takes part in the dynamics, and the field equation is properly written
with 
 , or
its generalization, as part of the
stress-energy tensor. One would then say that the differential
equation of gravity physics has not been changed from Einstein's
original form; instead there is a new component in the content of
the universe.
, or
its generalization, as part of the
stress-energy tensor. One would then say that the differential
equation of gravity physics has not been changed from Einstein's
original form; instead there is a new component in the content of
the universe.
Having taken it that the universe is static, Einstein did not write down the differential equation for a(t), and so did not see the instability. Friedmann (1922, 1924) found the evolving homogeneous solution, but had the misfortune to do it before the astronomy became suggestive. Slipher's measurements of the spectra of the spiral nebulae -- galaxies of stars -- showed most are shifted toward the red, and Eddington (1924, pp. 161-2) remarked that that might be a manifestation of the second, repulsive, term in Eq. (24). Lemaître (1927) introduced the relation between Slipher's redshifts and a homogeneous matter-filled expanding relativistic world model. He may have been influenced by Hubble's work that was leading to the publication in 1929 of the linear redshift-distance relation (eq. [5]): as a graduate student at MIT he attended a lecture by Hubble.
In Lemaître's (1927) solution the expanding universe traces asymptotically back to Einstein's static case. Lemaître then turned to what he called the primeval atom, and we would term a Big Bang model. This solution expands from densities so large as to require some sort of quantum treatment, passes through a quasi-static approximation to Einstein's solution, and then continues expanding to de Sitter's (1917) empty space solution. To modern tastes this "loitering" model requires incredibly special initial conditions, as will be discussed. Lemaître liked it because the loitering epoch allows the expansion time to be acceptably long for Hubble's (1929) estimate of H0, which is an order of magnitude high.
The record shows Einstein never liked the
 term. His
view of how general relativity might fit Mach's principle was
disturbed by
de Sitter's (1917)
solution to Eq. (34) for empty space
(Tµ
term. His
view of how general relativity might fit Mach's principle was
disturbed by
de Sitter's (1917)
solution to Eq. (34) for empty space
(Tµ = 0)
with
= 0)
with  > 0.
14,15
Pais (1982, p. 288)
points out that Einstein in a letter to Weyl in 1923 comments on the effect
of
> 0.
14,15
Pais (1982, p. 288)
points out that Einstein in a letter to Weyl in 1923 comments on the effect
of  in Eq. (24):
"According to
De Sitter two material points that are sufficiently far apart,
continue to be accelerated and move apart. If there is no
quasistatic world, then away with the cosmological term."
We do not know whether at this time Einstein was influenced by
Slipher's redshifts or Friedmann's expanding world model.
in Eq. (24):
"According to
De Sitter two material points that are sufficiently far apart,
continue to be accelerated and move apart. If there is no
quasistatic world, then away with the cosmological term."
We do not know whether at this time Einstein was influenced by
Slipher's redshifts or Friedmann's expanding world model.
The earliest published comments we have found on Einstein's
opinion of  within
the evolving world model
(Einstein, 1931;
Einstein and de Sitter,
1932)
make the point that, since
not all the terms in the expansion rate Eq. (11) are
logically required, and the matter term surely is present and
likely dominates over radiation at low redshift, a reasonable
working model drops
within
the evolving world model
(Einstein, 1931;
Einstein and de Sitter,
1932)
make the point that, since
not all the terms in the expansion rate Eq. (11) are
logically required, and the matter term surely is present and
likely dominates over radiation at low redshift, a reasonable
working model drops
 K0 and
K0 and

 0
and ignores
0
and ignores
 R0. This
simplifies the expansion rate equation to what has come to be
called the Einstein-de Sitter model,
R0. This
simplifies the expansion rate equation to what has come to be
called the Einstein-de Sitter model,
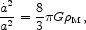 |
(35) |
where
 M is
the mass density in non-relativistic matter; here
M is
the mass density in non-relativistic matter; here
 M =
8
M =
8 G
G
 M /
(3H2) is unity.
The left side is a measure of the kinetic
energy of expansion per unit mass, and the right-hand side a
measure of the negative of the gravitational potential energy. In
effect, this model universe is expanding with escape velocity.
M /
(3H2) is unity.
The left side is a measure of the kinetic
energy of expansion per unit mass, and the right-hand side a
measure of the negative of the gravitational potential energy. In
effect, this model universe is expanding with escape velocity.
Einstein and de Sitter point out that Hubble's estimate of H0 and de Sitter's estimate of the mean mass density in galaxies are not inconsistent with Eq. (35) (and since both quantities scale with distance in the same way, this result is not affected by the error in the distance scale that affected Hubble's initial measurement of H0). But the evidence now is that the mass density is about one quarter of what is predicted by this equation, as we will discuss.
Einstein and de Sitter
(1932)
remark that the curvature term in
Eq. (11) is "essentially determinable,
and an increase in the precision of the data derived from
observations will enable us in the future to fix its sign and
determine its value." This is happening, 70 years later.
The cosmological constant term is measurable in principle, too,
and may now have been detected. But
Einstein and de Sitter say only that the theory of an expanding
universe with finite mean mass density "can be reached without
the introduction of"
 .
.
Further to this point, in the appendix of the second edition of
his book, The Meaning of Relativity,
Einstein (1945, p. 127)
states that the "introduction of the `cosmologic member'" --
Einstein's terminology for
 -- "into
the equations of
gravity, though possible from the point of view of relativity, is
to be rejected from the point of view of logical economy", and
that if "Hubble's expansion had been discovered at the time of
the creation of the general theory of relativity, the
cosmologic member would never have been introduced. It seems now
so much less justified to introduce such a member into the field
equations, since its introduction loses its sole original
justification, - that of leading to a natural solution of the
cosmologic problem."
Einstein knew that without the cosmological constant the
expansion time derived from Hubble's estimate of H0 is
uncomfortably short compared to estimates of the ages of the
stars, and opined that that might be a problem with the star
ages. The big error, the value of H0, was corrected by
1960
(Sandage, 1958,
1962).
-- "into
the equations of
gravity, though possible from the point of view of relativity, is
to be rejected from the point of view of logical economy", and
that if "Hubble's expansion had been discovered at the time of
the creation of the general theory of relativity, the
cosmologic member would never have been introduced. It seems now
so much less justified to introduce such a member into the field
equations, since its introduction loses its sole original
justification, - that of leading to a natural solution of the
cosmologic problem."
Einstein knew that without the cosmological constant the
expansion time derived from Hubble's estimate of H0 is
uncomfortably short compared to estimates of the ages of the
stars, and opined that that might be a problem with the star
ages. The big error, the value of H0, was corrected by
1960
(Sandage, 1958,
1962).
Gamow (1970, p. 44) recalls that "when I was discussing cosmological problems with Einstein, he remarked that the introduction of the cosmological term was the biggest blunder he ever made in his life." This certainly is consistent with all of Einstein's written comments we have seen on the cosmological constant per se; we do not know whether Einstein was also referring to the missed chance to predict the evolution of the universe.
13 To
help motivate the introduction of
 ,
Einstein (1917)
mentioned a modification of Newtonian gravity
physics that might make the theory well defined when the mass
distribution is homogeneous. In Einstein's example, similar to
what was considered by Seeliger and Neumann in the mid 1890s, the
modified field equation for the gravitational potential
,
Einstein (1917)
mentioned a modification of Newtonian gravity
physics that might make the theory well defined when the mass
distribution is homogeneous. In Einstein's example, similar to
what was considered by Seeliger and Neumann in the mid 1890s, the
modified field equation for the gravitational potential
 is
is
 2
2
 -
-

 =
4
=
4 G
G
 M.
This allows the nonsingular homogeneous static solution
M.
This allows the nonsingular homogeneous static solution
 =
- 4
=
- 4 G
G
 M /
M /
 . In this example the
potential for an isolated point mass is the Yukawa form,
. In this example the
potential for an isolated point mass is the Yukawa form,

 e-
e- 1/2r / r.
Trautman (1965)
points out that this is not the nonrelativistic
limit of general relativity with the cosmological term.
Rather, Eq. (24) follows from
1/2r / r.
Trautman (1965)
points out that this is not the nonrelativistic
limit of general relativity with the cosmological term.
Rather, Eq. (24) follows from
 2
2
 =
4
=
4 G(
G( M -
2
M -
2
 ),
where the active gravitational mass density of the
),
where the active gravitational mass density of the
 term
is
term
is 
 +
3p
+
3p = - 2
= - 2
 .
Norton (1999)
reviews the history of ideas of this
Seeliger-Neumann Yukawa-type potential in gravity physics.
Back.
.
Norton (1999)
reviews the history of ideas of this
Seeliger-Neumann Yukawa-type potential in gravity physics.
Back.
14
North (1965)
reviews the confused early history of ideas on the
possible astronomical significance of de Sitter's solution for an
empty universe with
 > 0; we add a
few comments on
the physics that contributed to the discovery of the expanding
world model. Suppose an observer in de Sitter's spacetime
holds a string tied to a source of light, so the source
stays at fixed physical distance r <<
H
> 0; we add a
few comments on
the physics that contributed to the discovery of the expanding
world model. Suppose an observer in de Sitter's spacetime
holds a string tied to a source of light, so the source
stays at fixed physical distance r <<
H -1. The
source is much less massive than the observer, the gravitational
frequency shift due to the observer's mass may be neglected, and
the observer is moving freely. Then the observer receives light
from the source shifted to the red by
-1. The
source is much less massive than the observer, the gravitational
frequency shift due to the observer's mass may be neglected, and
the observer is moving freely. Then the observer receives light
from the source shifted to the red by

 /
/
 = -
(H
= -
(H r)2 / 2. The observed
redshifts of particles moving on geodesics depend on the
initial conditions. Stars in the outskirts of our galaxy are held
at fixed mean distances from us by their transverse motions. The
mean shifts of the spectra of light from these stars include this
quadratic de Sitter term as well as the much larger Doppler and
ordinary gravitational shifts. The prescription for initial
conditions that reproduces the linear redshift-distance relation
for distant galaxies follows
Weyl's (1923)
principle: the world
particle geodesics trace back to a near common position in the
remote past, in the limiting case of the Friedmann-Lemaître
model at
r)2 / 2. The observed
redshifts of particles moving on geodesics depend on the
initial conditions. Stars in the outskirts of our galaxy are held
at fixed mean distances from us by their transverse motions. The
mean shifts of the spectra of light from these stars include this
quadratic de Sitter term as well as the much larger Doppler and
ordinary gravitational shifts. The prescription for initial
conditions that reproduces the linear redshift-distance relation
for distant galaxies follows
Weyl's (1923)
principle: the world
particle geodesics trace back to a near common position in the
remote past, in the limiting case of the Friedmann-Lemaître
model at  M0
M0
 0. This spatially
homogeneous coordinate
labeling of de Sitter's spacetime, with space sections with
negative curvature, already appears in
de Sitter (1917,
Eq. [15]), and is repeated in
Lanczos (1922).
This line element is the second expression in our Eq. (15) with
a
0. This spatially
homogeneous coordinate
labeling of de Sitter's spacetime, with space sections with
negative curvature, already appears in
de Sitter (1917,
Eq. [15]), and is repeated in
Lanczos (1922).
This line element is the second expression in our Eq. (15) with
a  cosh H
cosh H t.
Lemaître (1925) and
Robertson (1928)
present the coordinate labeling for the
spatially-flat case, where the line element is
ds2 = dt2 -
e2H
t.
Lemaître (1925) and
Robertson (1928)
present the coordinate labeling for the
spatially-flat case, where the line element is
ds2 = dt2 -
e2H t(dx2 + dy2
+ dz2) (in the
choice of symbols and signature in Eqs. [15] and [27]).
Lemaître (1925) and
Robertson (1928)
note that
particles at rest in this coordinate system present a linear
redshift-distance relation, v =
H
t(dx2 + dy2
+ dz2) (in the
choice of symbols and signature in Eqs. [15] and [27]).
Lemaître (1925) and
Robertson (1928)
note that
particles at rest in this coordinate system present a linear
redshift-distance relation, v =
H r, at small v.
Robertson (1928)
estimated
H
r, at small v.
Robertson (1928)
estimated
H ,
and Lemaître
(1927)
its analog for the Friedmann-Lemaître model, from
published redshifts and Hubble's galaxy distances. Their
estimates are not far off
Hubble's (1929)
published value.
Back.
,
and Lemaître
(1927)
its analog for the Friedmann-Lemaître model, from
published redshifts and Hubble's galaxy distances. Their
estimates are not far off
Hubble's (1929)
published value.
Back.
15 To the present way of thinking the lengthy debate about the singularity in de Sitter's static solution, chronicled in North (1965), seems surprising, because de Sitter (1917) and Klein (1918) had presented de Sitter's solution as a sphere embedded in 4 plus 1 dimensional flat space, with no physical singularity. Back.