B. The development of ideas

1. Early indications of

In the classic book, The Classical Theory of Fields, Landau and Lifshitz (1951, p. 338) second Einstein's opinion of the cosmological constant , stating there is "no basis whatsoever" for adjustment of the theory to include this term. The empirical side of cosmology is not much mentioned in this book, however (though there is a perceptive comment on the limited empirical support for the homogeneity assumption; p. 332). In the Supplementary Notes to the English translation of his book, Theory of Relativity, Pauli (1958, p. 220) also endorses Einstein's position.

Discussions elsewhere in the literature on how one might find empirical constraints on the values of the cosmological parameters usually take account of . The continued interest was at least in part driven by indications that might be needed to reconcile theory and observations. Here are three examples.

First, the expansion time is uncomfortably short if = 0. Sandage's recalibration of the distance scale in the 1960s indicates H₀ 75 km s^-1 Mpc^-1. If = 0 this says the time of expansion from densities too high for stars to have existed is < H₀^-1 13 Gyr, maybe less than the ages of the oldest stars, then estimated to be greater than about 15 Gyr. Sandage (1961a) points out that the problem is removed by adding a positive . The present estimates reviewed below (Sec. IV.B.3) are not far from these numbers, but still too uncertain for a significant case for .

Second, counts of quasars as a function of redshift show a peak at z ~ 2, as would be produced by the loitering epoch in Lemaître's model (Petrosian, Salpeter, and Szekeres, 1967; Shklovsky, 1967; Kardashev, 1967). The peak is now well established, centered at z ~ 2.5 (Croom et al., 2001; Fan et al., 2001). It usually is interpreted as the evolution in the rate of violent activity in the nuclei of galaxies, though in the absence of a loitering epoch the indicated sharp variation in quasar activity with time is curious (but certainly could be a consequence of astrophysics that is not well understood).

The third example is the redshift-magnitude relation. Sandage's (1961a) analysis indicates this is a promising method of distinguishing world models. The Gunn and Oke (1975) measurement of this relation for giant elliptical galaxies, with Tinsley's (1972) correction for evolution of the star population from assumed formation at high redshift, indicates curvature away from the linear relation in the direction that, as Gunn and Tinsley (1975) discuss, could only be produced by (within general relativity theory). The new application of the redshift-magnitude test, to Type Ia supernovae (Sec. IV.B.4), is not inconsistent with the Gunn-Oke measurement; we do not know whether this agreement of the measurements is significant, because Gunn and Oke were worried about galaxy evolution. ¹⁶

2. The coincidences argument against

An argument against an observationally interesting value of , from our distrust of accidental coincidences, has been in the air for decades, and became very influential in the early 1980s with the introduction of the inflation scenario for the very early universe.

If the Einstein-de Sitter model in Eq. (35) were a good approximation at the present epoch, an observer measuring the mean mass density and Hubble's constant when the age of the universe was one tenth the present value, or at ten times the present age, would reach the same conclusion, that the Einstein-de Sitter model is a good approximation. That is, we would flourish at a time that is not special in the course of evolution of the universe. If on the other hand two or more of the terms in the expansion rate equation (11) made substantial contributions to the present value of the expansion rate, it would mean we are present at a special epoch, because each term in Eq. (11) varies with the expansion factor in a different way. To put this in more detail, we imagine that the physics of the very early universe, when the relativistic cosmological model became a good approximation, set the values of the cosmological parameters. The initial values of the contributions to the expansion rate equation had to have been very different from each other, and had to have been exceedingly specially fixed, to make two of the _i0's have comparable values. This would be a most remarkable and unlikely-looking coincidence. The multiple coincidences required for the near vanishing of and at a redshift not much larger than unity makes an even stronger case against Lemaître's coasting model, by this line of argument.

The earliest published comment we have found on this point is by Bondi (1961, p. 166), in the second edition of his book Cosmology. Bondi notes the "remarkable property" of the Einstein-de Sitter model: the dimensionless parameter we now call _M is independent of the time at which it is computed (since it is unity). The coincidences argument follows and extends Bondi's comment. It is presented in McCrea (1971, p. 151). When Peebles was a postdoc, in the early 1960s, in R. H. Dicke's gravity research group, the coincidences argument was discussed, but published much later (Dicke, 1970, p. 62; Dicke and Peebles, 1979). We do not know its provenance in Dicke's group, whether from Bondi, McCrea, Dicke, or someone else. We would not be surprised to learn others had similar thoughts.

The coincidences argument is sensible but not a proof, of course. The discovery of the 3 K thermal cosmic microwave background radiation gave us a term in the expansion rate equation that is down from the dominant one by four orders of magnitude, not such a large factor by astronomical standards. This might be counted as a first step away from the argument. The evidence from the dynamics of galaxies that _M0 is less than unity is another step (Peebles, 1984, p. 442; 1986). And yet another is the development of the evidence that the and dark matter terms differ by only a factor of three (Eq. [2]). This last is the most curious, but the community has come to accept it, for the most part. The precedent makes Lemaître's coasting model more socially acceptable.

A socially acceptable value of cannot be such as to make life impossible, of course. ¹⁷ But perhaps the most productive interpretation of the coincidences argument is that it demands a search for a more fundamental underlying model. This is discussed further in Sec. III.E and the Appendix.

3. Vacuum energy and

Another tradition to consider is the relation between and the vacuum or dark energy density. In one approach to the motivation for the Einstein field equation, taken by McVittie (1956) and others, appears as a constant of integration (of the expression for local conservation of energy and momentum). McVittie (1956, p. 35) emphasizes that, as a constant of integration, "cannot be assigned any particular value on a priori grounds." Interesting variants of this line of thought are still under discussion (Weinberg, 1989; Unruh, 1989, and references therein).

The notion of as a constant of integration may be related to the issue of the zero point of energy. In laboratory physics one measures and computes energy differences. But the net energy matters for gravity physics, and one can imagine represents the difference between the true energy density and the sum one arrives at by laboratory physics. Eddington (1939) and Lemaître (1934, 1949) make this point.

Bronstein (1933) ¹⁸ carries the idea further, allowing for transfer of energy between ordinary matter and that represented by . In our notation, Bronstein expresses this picture by generalizing Eq. (9) to

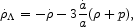(36)

where and p are the energy density and pressure of ordinary matter and radiation. Bronstein goes on to propose a violation of local energy conservation, a thought that no longer seems interesting. North (1965, p. 81) finds Eddington's (1939) interpretation of the zero of energy also somewhat hard to defend. But for our purpose the important point is that the idea of as a form of energy has been in the air, in at least some circles, for many years.

The zero-point energy of fields contributes to the dark energy density. To make physical sense the sum over the zero-point mode energies must be cut off at a short distance or a high frequency up to which the model under consideration is valid. The integral of the zero-point energy (k / 2) of normal modes (of wavenumber k) of a massless real bosonic scalar field (), up to the wavenumber cutoff k_c, gives the vacuum energy density quantum-mechanical expectation value ¹⁹

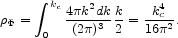(37)

Nernst (1916) seems to have been the first to write down this equation, in connection with the idea that the zero-point energy of the electromagnetic field fills the vacuum, as a light aether, that could have physically significant properties. ²⁰ This was before Heisenberg and Schrödinger: Nernst's hypothesis is that each degree of freedom, which classical statistical mechanics assigns energy kT/2, has "Nullpunktsenergie" h / 2. This would mean the ground state energy of a one-dimensional harmonic oscillator is h, twice the correct value. Nernst's expression for the energy density in the electromagnetic field thus differs from Eq. (37) by a factor of two (after taking account of the two polarizations), which is wonderfully close. For a numerical example, Nernst noted that if the cutoff frequency were = 10²⁰ Hz, or ~ 0.4 MeV, the energy density of the "Lichtäther" (light aether) would be 10²³ erg cm^-3, or about 100 g cm^-3.

By the end of the 1920s Nernst's hypothesis was replaced with the demonstration that in quantum mechanics the zero-point energy of the vacuum is as real as any other. W. Pauli, in unpublished work in the 1920s, ²¹ repeated Nernst's calculation, with the correct factor of 2, taking k_c to correspond to the classical electron radius. Pauli knew the value of is quite unacceptable: the radius of the static Einstein universe with this value of "would not even reach to the moon" (Rugh and Zinkernagel, 2000, p. 5). ²² The modern version of this "physicists' cosmological constant problem" is even more acute, because a natural value for k_c is thought to be much larger than what Nernst or Pauli used. ²³

While there was occasional discussion of this issue in the middle of the 20^th century (as in the quote from N. Bohr in Rugh and Zinkernagel, 2000, p. 5), the modern era begins with the paper by Zel'dovich (1967) that convinced the community to consider the possible connection between the vacuum energy density of quantum physics and Einstein's cosmological constant. ²⁴

If the physics of the vacuum looks the same to any inertial observer its contribution to the stress-energy tensor is the same as Einstein's cosmological constant (Eq. [19]). Lemaître (1934) notes this: "in order that absolute motion, i.e., motion relative to the vacuum, may not be detected, we must associate a pressure p = - c² to the energy density c² of vacuum". Gliner (1965) goes further, presenting the relation between the metric tensor and the stress-energy tensor of a vacuum that appears the same to any inertial observer. But it was Zel'dovich (1968) who presented the argument clearly enough and at the right time to catch the attention of the community.

With the development of the concept of broken symmetry in the now standard model for particle physics came the idea that the expansion and cooling of the universe is accompanied by a sequence of first-order phase transitions accompanying the symmetry breaking. Each first-order transition has a latent heat that appears as a contribution to an effective time-dependent (t) or dark energy density. ²⁵ The decrease in value of the dark energy density at each phase transition is much larger than an acceptable present value (within relativistic cosmology); the natural presumption is that the dark energy is negligible now. This final condition seems bizarre, but the picture led to the very influential concept of inflation. We discussed the basic elements in connection with Eq. (27); we turn now to some implications.

¹⁶ Early measurements of the redshift-magnitude relation were meant in part to test the Steady State cosmology of Bondi and Gold (1948) and Hoyle (1948). Since the Steady State cosmology assumes spacetime is independent of time its line element has to have the form of the de Sitter solution with _K0 = 0 and the expansion parameter in Eq. (27). The measured curvature of the redshift-magnitude relation is in the direction predicted by the Steady State cosmology. But this cosmology fails other tests discussed in Sec. IV.B. Back.

¹⁷ If were negative and the magnitude too large there would not be enough time for the emergence of life like us. If were positive and too large the universe would expand too rapidly to allow galaxy formation. Our existence, which requires something resembling the Milky Way galaxy to contain and recycle heavy elements, thus provides an upper bound on the value of . Such anthropic considerations are discussed by Weinberg (1987, 2001), Vilenkin (2001), and references therein. Back.

¹⁸ Kragh (1996, p. 36) describes Bronstein's motivation and history. We discuss this model in more detail in Sec. III.E, and comment on why decay of dark energy into ordinary matter or radiation would be hard to reconcile with the thermal spectrum of the 3 K cosmic microwave background radiation. Decay into the dark sector may be interesting. Back.

¹⁹ Eq. (37), which usually figures in discussions of the vacuum energy puzzle, gives a helpful indication of the situation: the zero-point energy of each mode is real and the sum is large. The physics is seriously incomplete, however. The elimination of spatial momenta with magnitudes k > k_c only makes sense if there is a preferred reference frame in which k_c is defined. Magueijo and Smolin (2002) mention a related issue: In which reference frame is the Planck momentum of a virtual particle at the threshold for new phenomena? In both cases one may implicitly choose the rest frame for the large-scale distribution of matter and radiation. It seems strange to think the microphysics cares about large-scale structure, but maybe it happens in a sea of interacting fields. The cutoff in Eq. (37) might be applied at fixed comoving wavenumber k_c a(t)^-1, or at a fixed physical value of k_c. 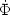The first prescription can be described by an action written as a sum of terms 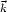² / 2 + k^{2 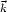2} / (2a(t)²) for the allowed modes. The zero-point energy of each mode scales with the expansion of the universe as a(t)^-1, and the sum over modes scales as a(t)^-4, consistent with k_c a(t)^-1. In the limit of exact spatial homogeneity, an equivalent approach uses the spatial average of the standard expression for the field stress-energy tensor. Indeed, DeWitt (1975) and Akhmedov (2002) show that the vacuum expectation value of the stress-energy tensor, expressed as an integral cut off at k = k_c, and computed in the preferred coordinate frame, is diagonal with space part p = / 3, for the massless field we are considering. That is, in this prescription the vacuum zero point energy acts like a homogeneous sea of radiation. This defines a preferred frame of motion, where the stress-energy tensor is diagonal, which is not unexpected because we need a preferred frame to define k_c. It is unacceptable as a model for the properties of dark energy, of course. For example, if the dark energy density were normalized to the value now under discussion, and varied as a(t)^-4, it would quite mess up the standard model for the origin of the light elements. We get a more acceptable model for the behavior of from the second prescription, with the cutoff at a fixed physical momentum. If we also want to satisfy local energy conservation we must take the pressure to be p = - . This does not contradict the derivation of p in the first prescription, because the second situation cannot be described by an action: the pressure must be stipulated, not derived. What is worse, the known fields at laboratory momenta certainly do not allow this stipulation; they are well described by analogs of the action in the first prescription. This quite unsatisfactory situation illustrates how far we are from a theory of the vacuum energy. Back.

²⁰ A helpful discussion of Nernst's ideas on cosmology is in Kragh (1996, pp. 151-7). Back.

²¹ This is discussed in Enz and Thellung (1960), Enz (1974), Rugh and Zinkernagel (2000, pp. 4-5), and Straumann (2002). Back.

²² In an unpublished letter in 1930, G. Gamow considered the gravitational consequences of the Dirac sea (Dolgov, 1990, p. 230). We thank A. Dolgov for helpful correspondence on this point. Back.

²³ In terms of an energy scale defined by = ⁴, the Planck energy G^-1/2 is about 30 orders of magnitude larger than the "observed" value of . This is, of course, an extreme case, since a lot of the theories of interest break down well below the Planck scale. Furthermore, in addition to other contributions, one is allowed to add a counterterm to Eq. (37) to predict any value of . With reference to this point, it is interesting to note that while Pauli did not publish his computation of , he remarks in his famous 1933 Handbuch der Physik review on quantum mechanics that it is more consistent to "exclude a zero-point energy for each degree of freedom as this energy, evidently from experience, does not interact with the gravitational field" (Rugh and Zinkernagel, 2000, p. 5). Pauli was fully aware that one must take account of zero-point energies in the binding energies of molecular structure, for example (and we expect he was aware that what contributes to the energy contributes to the gravitational mass). He chose to drop the section with the above comment from the second (1958) edition of the review (Pauli, 1980, pp. iv-v). In a globally supersymmetric field theory there are equal numbers of bosonic and fermionic degrees of freedom, and the net zero-point vacuum energy density vanishes (Iliopoulos and Zumino, 1974; Zumino, 1975). However, supersymmetry is not a symmetry of low energy physics, or even at the electroweak unification scale. It must be broken at low energies, and the proper setting for a discussion of the zero-point in this case is locally supersymmetric supergravity. Weinberg (1989, p. 6) notes "it is very hard to see how any property of supergravity or superstring theory could make the effective cosmological constant sufficiently small". Witten (2001) and Ellwanger (2002) review more recent developments on this issue in the superstring/M theory/branes scenario. Back.

²⁴ For subsequent more detailed discussions of this issue, see Zel'dovich (1981), Weinberg (1989), Carroll, Press, and Turner (1992), Sahni and Starobinsky (2000), Carroll (2001), and Rugh and Zinkernagel (2000). Back.

²⁵ Early references to this point are Linde (1974), Dreitlein (1974), Kirzhnitz and Linde (1974), Veltman (1975), Bludman and Ruderman (1977), Canuto and Lee (1977), and Kolb and Wolfram (1980). Back.