11.2.1. The Data

a) Hydrogen Mass

The mass of neutral hydrogen galaxy is derived from its 21-cm emission spectrum. The surface density (atom cm^-2) of hydrogen radiating in a 1 km sec^-1 interval is given by

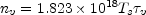(1)

where T_s is the spin temperature of the gas, and _v the optical depth (see, for example, Chapter 2).

T_s is assumed here to be constant along Galactic and Extra-Galactic Radio Astronomy the column of radiating gas. If the gas is optically thin (T_B << T_s), then the surface density is given by

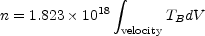(2)

and the total number of atoms, N, is obtained by integrating the surface density across the galaxy

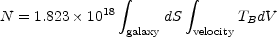(3)

An element of surface area dS is related to the distance D by dS = D² d. Thus the number of atoms is proportional to D² and the integrated line flux is given by

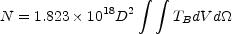(4)

or in convenient units,

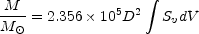(5)

where D is in Mpc, S_v in flux units ¹, and dV in km sec^-1.

The assumption of small optical depth may be invalid, particularly where the velocity dispersion of the gas is small or the line of-sight thickness is large owing to the high inclination of the galaxy. In this case the mass of neutral hydrogen derived above is a lower limit. Also, the variation of T_s (known to occur in our galaxy) makes the mass a lower limit from another point of view, as some of the hydrogen will be in cold clouds of substantial opacity. It is tacitly assumed that there is no interaction between radio continuum and line radiation. Epstein (1964) has considered these problems for different cases.

b) Total Masses

The masses of spiral galaxies are estimated by assuming that the galaxies are in rotational equilibrium. The line-of-sight velocity of some component of the galaxy - usually neutral hydrogen or ionized hydrogen, oxygen, and nitrogen - can be measured by the Doppler shift of its corresponding line emission. In the case of irregular galaxies (or for low-resolution neutral hydrogen measurements) the mass of the galaxy can be estimated (e.g., Bottinelli et al., 1968) directly from the measured velocity dispersion using the virial theorem (Chandrasekhar, 1942). More usually, for spiral galaxies a rotation velocity is estimated as a function of radius and a mass is derived from a model for the centrifugal equilibrium of the gas. The basic equation is of the same form in either case and the estimated mass scales linearly with the assumed distance to the galaxy. Assuming that the galaxy is a plane rotating disk in centrifugal equilibrium, a simple Keplerian estimate of the total mass is obtained as M_T = (rv² / G), where the maximum rotational velocity v occurs at a radius r. In convenient units this gives

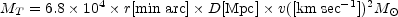(6)

As discussed in more detail in Sections 11.5 and 11.6, the neutral hydrogen data usually have poor angular resolution and the total mass must be derived from a model for the rotation curve. The optical data, however, have high angular resolution and provide a detailed mass distribution, but only out to the limiting radius of the emission lines (e.g., Burbidge, Burbidge, and Prendergast, 1963). There is some difficulty, then, in comparing masses derived from optical and radio data.

c) Luminosity

The measured luminosity of a galaxy increases with the area of the photographic image integrated. The Holmberg (1958) system of luminosities and diameters of galaxies provides a well-defined measurement down to a sky-brightness-limited isophote of 26.^m5 per square second arc. The measured luminosities and colors on the UBV system can be corrected for an average galactic extinction by -0.25 cosec (latitude) and for inclination of the observed galaxy. The absolute luminosity of a galaxy is usually quoted in units of the solar luminosity and of course scales as the square of the assumed distance.

d) Selection Effects

Observational requirements force a selection of galaxies which may affect the correlations described below. The neutral hydrogen measurements are biased toward the late-type (Sc and Irr) galaxies and optical measurements of rotation curves tend to be of intrinsically bright galaxies. Upper limits for the HI-to-total mass ratio of 0.1% have been established for several elliptical galaxies (Bottinelli et al. 1973), and we shall confine ourselves in what follows to the spiral and irregular galaxies.

¹ 1 flux unit = 10^-26 Wm^-2 Hz^-1. Back.