11.6.1. Observational Requirements
a) Angular Resolution
Model fitting of low-resolution maps or of simple interferometer observations is clearly inadequate to analyze the details of the HI distribution and kinematics in spiral galaxies. Aspects concerning the spiral structure can be investigated only when we have obtained a map of the neutral hydrogen distribution with a resolution comparable to the angular separation of the luminous spiral arms. In the nearest galaxies this is of the order of 1 minute arc, and such resolution can at present be obtained only by the use of aperture synthesis techniques. Aperture synthesis observations of external galaxies are currently being made at four observatories. The instruments being used are the Cambridge Half-Mile Telescope in England (Baldwin et al. 1971), the 12-element Westerbork Synthesis Radio Telescope (Brouw, 1971) in the Netherlands, the 2-element interferometer at the Owens Valley Radio Observatory, and the 3-element interferometer at the National Radio Astronomy Observatory (NRAO) in the United States.
Observations are usually made with the telescopes at each of several
separations at which the telescopes track the source over a
range of hour angle. Maps of the sky brightness are computed from a
Fourier inversion of the recorded data. This is the method of
Earth rotation synthesis (see Chapter 10). The maximum angular
resolution is determined by the largest interferometer baseline,
D, used in the aperture synthesis. The synthesized
beam subtends a solid angle
(
/ D)2
cosec
,
where is the
declination of the source.
If observations are made with interferometer baselines at intervals d
to a maximum D, then a grating sidelobe response occurs
at an angle
/ d in
RA and
( / d ) ×
cosec
in declination. The area of sky which can be
mapped without ambiguity from grating side-lobes is
( /
d)2 cosec
. The baseline interval,
d, should be sufficiently small that this area includes the
extent of the neutral hydrogen radiating in any velocity channel;
otherwise the synthesized map will be confused by
grating sidelobes. There is no point, however, in making d much smaller
than the diameter of the antennas, since the reception pattern
of these then limits the area of sky which can be mapped.
b) Frequency Resolution
Observations of spiral galaxies show that the greatest range of velocities expected is about ± 300 km sec-1, and it is desirable that a multi-channel receiver should cover the whole of this range. The maximum useful resolution in velocity is dependent on the angular size of the synthesized beam, since in general the line-of-sight radial velocity varies in a systematic way across the galaxy. Near the center of the galaxy the area of the synthesized beam intersects many isovelocity contours (see Figure 11.2); a large range of velocities is present within one beam area, and a high-velocity resolution is not required. Further out in the galaxy, however, there is a small range of rotation velocities within one beam area and a higher resolution might be useful. Dispersion in the gas along the line of sight might be of order 10 km sec-1 and this accordingly is a useful resolution. Thus a desirable minimum for a multi-channel receiver is 60 channels, each 10 km sec-1 wide, for each interferometer.
c) Sensitivity
Suppose that we spend equal times observing at each interferometer
baseline at intervals d to a maximum D. The total integration time is
proportional to D / d. The angular resolution obtained
is proportional to 
=
/ D so that
for a given stepping interval d
(which is determined by the angular extent of
the hydrogen) the fluctuations in aerial temperature,
Ta, are proportional to
1/2. As a
result of the aperture synthesis, only flux
collected by the synthesized beam contributes
to the effective aerial temperature of the
source. The aerial temperature, Ta, due to a
source of uniform brightness temperature,
Tb, is obtained by multiplying Tb by
the ratio of the synthesized beam area to the antenna beam area. Thus
Ta 
Tb
2, and the
sensitivity of the
telescope to extended objects decreases with resolution as
 |
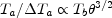(11) |
This degrading of the signal-to-noise ratio with increasing resolution can be offset by spending a longer time at the larger aerial spacing, and the reason for this requirement may be understood in terms of the increased rate of sampling of the (u - v) plane at the longer baselines (see Chapter 10). It does, however, mean that the sensitivity requirements may limit the resolution rather than the available baseline.