11.3.2. Velocity Distribution

a) Line-of-Sight Velocity

Observations of neutral hydrogen are usually made with a multi-channel spectrometer so that the frequency or velocity distribution of the line radiation is also determined. Neutral hydrogen-line radiation arises from a forbidden transition, and the low-transition probability implies a small natural width of the line (5 × 10^-16 Hz). The observed width of the line is therefore due to Doppler broadening (-4.74 kHz / km sec^-1) at the line rest frequency of 1420.4 MHz.

The line broadening is partly due to random and thermal motions in the gas, but is mainly due to larger-scale motions of the gas. In a spiral galaxy the dominant motion is one of rotation, although expansion motions and other "peculiar" velocities are of great interest. The line-of-sight velocity of the neutral hydrogen in any portion of the galaxy can be measured as a Doppler shift, and with sufficient angular and frequency resolution we observe different Doppler shifts across the face of the galaxy. The line-of-sight velocity is interpreted in terms of the rotation, expansion, and other velocities in the galaxy, which is assumed to have a plane rotating disk geometry.

b) Isovelocity Contours

The observed line-of-sight velocity u(r, ) of hydrogen with azimuthal coordinates (r, ) in a plane galaxy inclined at an angle i to the plane of the sky is given by

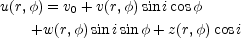(7)

where v₀ is the systemic velocity, v(r, ) the tangential velocity (including both the rotation of the galaxy and "peculiar" streaming and random components), w(r, ) a radial velocity in the plane of the galaxy, and z(r, ) a velocity out of the plane of the galaxy. A complete analysis of the kinematics of a galaxy should include all these effects. If the motion of the hydrogen in a galaxy is one of pure rotation, then the lines of constant observed radial velocity will be the lines

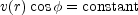(8)

A plot of v(r) against radius r is called the rotation curve for the galaxy and typically has the form shown in Figure 11.1. For a rotation curve of this form the lines of constant observed velocity (the isovelocity contours) will have the form shown in Figure 11.2. Where the rotation is solid-body, i.e., v(r) r, the isovelocity contours are parallel to the minor axis of the galaxy. The region of solid-body rotation is shown enclosed by the dashed line in Figure 11.2. Other systematic motions of the galaxy have characteristic isovelocity contours; e.g., the addition of an expansion, w(r) r, gives isovelocity contours in the solid-body region inclined at an angle to the minor axis. Closed isovelocity contours are produced by the region of the rotation curve where the rotation velocity is decreasing with radius.

Figure 11.1. Model rotation curve showing (1) solid-body rotation out to 3 units radius, (2) constant velocity region between radii 3 and 4, (3) region of decreasing rotation velocity. (M. C. H. Wright.)

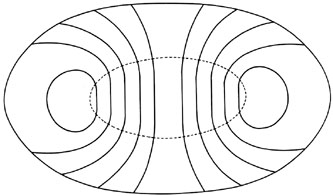Figure 11.2. Isovelocity contours (lines of constant line-of-sight velocity) in a rotating galaxy. The contours are drawn at intervals of the units of velocity in Figure 11.1 The region of solid-body rotation is shown enclosed by the dashed line. [M. C. H. Wright, Astrophys. J. (1971) 166:455.]

The highest physical resolution so far obtained has been the observations of the Magellanic Clouds with the 210-foot Parkes dish, where the half-power bandwidth is equivalent to about 200 pc at the distance of the clouds. In order to obtain comparable resolution in the nearest spiral galaxies an angular resolution of the order of 1 minute arc is required and we must resort to aperture synthesis techniques. Aperture synthesis in general is discussed in Chapter 10, and its application to spectral-line work is discussed in Section 11.6, but let us first see what has been achieved with single dish measurements.