11.6.2. Correlation Receivers

The requirement for a large number of velocity channels has favored the use of cross-correlation receivers. The principle on which the cross-correlation receiver operates is that, for two random time-varying signals, V₁(t) and V₂(t), the cross-correlation function

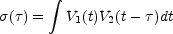(12)

is the Fourier transform of the visibility spectrum V₁() V₂() of the two signals. Here the signals V₁(t) and V₂(t) are the voltages from the two telescopes forming the interferometer, and V₁() V₂() is the cross-correlated spectrum at an angular frequency . The cross-correlation function is sampled over a range of delays ± T, ± 2T, . . . to a maximum delay ± T sec, and the visibility spectrum is obtained as the Fourier transform of the sampled cross-correlation function.

The maximum delay T determines the resolution of the synthesized frequency channel, 1/2T Hz, and the sampling interval AT produces a grating response in frequency at an interval 1/2T. The exact shape of the equivalent frequency filter is the Fourier transform of the weighting applied to the cross-correlation function. If the latter is transformed with equal weight applied to each delay, then the equivalent frequency filters have a (sin ) / response, with a half-width of 1.2 / 2T Hz and 22% sidelobes. Both positive and negative delays must be sampled to determine the amplitude and phase of the interferometer, and the correlation receiver is equivalent to a bank of T / T adjacent frequency filters at intervals of 1 / T Hz.

The cross-correlation may be achieved in practice either in an analogue device using physical delay steps or in a digital correlator. In the latter, simplified logic results if one-bit sampling of the correlation function is employed (so that only the sign of the sampled correlation function is recorded). This results in some loss in signal-to-noise ratio, but the visibility spectrum may be fully restored (Weinreb, 1963) through the Van Flyck correction. While increasing the complexity of the data processing, as an extra Fourier transform must be computed, the correlation receiver has a number of advantages over a conventional filter bank receiver in that the relative sensitivity of the frequency channels is easily calibrated. A digital correlator has good stability essential for a good synthesis, and the additional advantage that the bandwidth can be changed by simply changing the clock rate which determines the sampling interval.