2. CONSTRAINTS FROM THE KRAMERS-KRONIG RELATION

As already mentioned in Section 1, with specific assumptions made concerning the grain size, shape, geometry and composition, in principle one can calculate the absorption cross section C_abs and the opacity _abs as a function of wavelength. But this is limited to spherical grains; even for grains with such simple shapes as spheroids and cylinders, the calculation is complicated and limited to small size parameters defined as 2 a / . As a result, astronomers often adopt a simplified formula

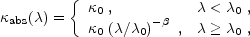(1)

where ₀ and the exponent index are usually treated as free parameters, while ₀ is often taken from experimental measurements of cosmic dust analogs or values predicted from interstellar dust models; or

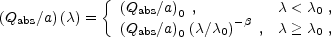(2)

where again ₀ and are free parameters and (Q_abs / a)₀ is usually taken from model calculations.

The Kramers-Kronig dispersion relation, originally deduced by Kronig [33] and Kramers [32] from the classical Lorentz theory of dispersion of light, connects the real (m'; dispersive) and imaginary (m''; absorptive) parts of the index of refraction (m[] = m' + i m'') based on the fundamental requirement of causality. Purcell [55] found that the Kramers-Kronig relation can be used to relate the extinction cross section integrated over the entire wavelength range to the dust volume V

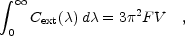(3)

where C_ext is the extinction cross section, and F, a dimensionless factor, is the orientationally-averaged polarizability relative to the polarizability of an equal-volume conducting sphere, depending only upon the grain shape and the static (zero-frequency) dielectric constant ₀ of the grain material (Purcell [55]; Draine [18]). Since C_ext is the sum of the absorption C_abs and scattering C_abs cross sections both of which are positive numbers at all wavelengths, replacing C_ext by C_abs in the left-hand-side of Eq. (3) would give a lower limit on its right-hand-side; therefore we can write Eq. (3) as

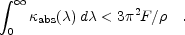(4)

It is immediately seen in Eq. (4) that should be larger than 1 for since F is a finite number and the integration in the left-hand-side of Eq. (4) should be convergent (also see Emerson [23]), although we cannot rule out 1 over a finite range of wavelengths.

Astronomers often use the opacity _abs of the formula described in Eq. (1) to fit the far-IR, submm and mm photometric data and then estimate the dust mass of interstellar clouds:

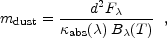(5)

where d is the distance of the cloud, T is the dust temperature, F is the measured flux density at wavelength . By fitting the photometric data points, one first derives the best-fit parameters , ₀, and T. For a given ₀, one then estimates m_dust from Eq. (5). In this way, various groups of astronomers have reported the detection of appreciable amounts of very cold dust (T < 10 K) both in the Milky Way and in external galaxies (Reach et al. [56]; Chini et al. [14]; Krügel et al. [35]; Siebenmorgen, Krügel, & Chini [59]; Boulanger et al. [10]; Popescu et al. [54]; Galliano et al. [24]; Dumke, Krause, & Wielebinski [20]).

As can be seen in Eq. (5), if the dust temperature is very low, one then has to invoke a large amount of dust to account for the measured flux densities. This often leads to too large a dust-to-gas ratio to be consistent with that expected from the metallicity of the region where the very cold dust is detected (e.g. see Dumke et al. [20]), unless the opacity _abs is very large. It has been suggested that such a large _abs can be achieved by fractal or porous dust (Reach et al. [56]; Dumke et al. [20]). Can _abs be really so large for physically realistic grains? At a first glance of Eq. (4), this appears plausible if the dust is sufficiently porous (so that its mass density is sufficiently small). However, one should keep in mind that for a porous grain, the decrease in will be offset by a decrease in F because the effective static dielectric constant ₀ becomes smaller when the dust becomes porous, leading to a smaller F factor (see Fig. 1 in Purcell [55] and Fig. 15 in Draine [18]).

Similarly, if one would rather use Q_abs / a of Eq. (2) instead of _abs of Eq. (1), we can also apply the Kramers-Kronig relation to place (1) a lower limit on - cannot be smaller than or equal to 1 at all wavelengths, and (2) an upper limit on (Q_abs / a)₀ from

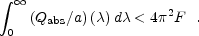(6)

Finally, the best-fit parameters , ₀, and T should be physically reasonable. This can be checked by comparing the best-fit temperature T with the dust equilibrium temperature T_d calculated from the energy balance between absorption and emission

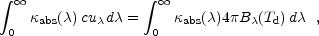(7)

where c is the speed of light, and u is the energy density of the radiation field. Alternatively, one can check whether the strength of the radiation field required by T_d T is in good agreement with the physical conditions of the environment where the dust is located.