It is seen in Section 2 that the Kramers-Kronig
relation
requires 
> 1 for 
.
For the Milky Way diffuse ISM, the 100 µm-1mm dust
emission spectrum obtained by
the Diffuse Infrared Background Experiment (DIRBE)
instrument on the Cosmic Background Explorer (COBE)
satellite is well fitted by the product of a single Planck curve of
T 
17.5 K and
an opacity law characterized by
2 (i.e.
abs
-2;
Boulanger et al. [10]),
although other sets of T
and are also
able to provide (almost) equally good fits to the observed emission
spectrum (e.g.
T 19.5 K and
1.7; see
Draine [17]).
But we should emphasize here that it is never flatter
than
1.65
(Draine [17]).
Smaller in
the submm and mm wavelength range has been reported for cold molecular
cores (e.g.
Walker et al. [63]:
0.9 - 1.8),
circumstellar disks around young stars (e.g.
Beckwith & Sargent [4]:
- 1-1;
Mannings & Emerson [47]:
0.6;
Koerner, Chandler, &
Sargent [28]:
0.6),
and circumstellar envelopes around evolved stars (e.g.
Knapp, Sandell, & Robson
[27]:
0.9)
including the prototypical carbon star IRC+10126
(Campbell et al. [13]:
1).
However, these results are not unique since the dust
temperature and density gradients in the clouds, disks
or envelopes have not been taken into account
in deriving
- the
exponent was usually estimated by fitting the submm and mm spectral
energy distribution by a modified black-body
-
B(T) under the "optically-thin"
assumption, with
and T
as adjustable parameters. If the dust spatial distribution is not
constrained, the very same emission spectrum can be equally well fitted
by models with different
values.
As a matter of fact, an asymptotic value of
2 (i.e.
abs
-2) is
expected for both dielectric and conducting spherical grains:
in the Rayleigh regime (where the wavelength is much
larger than the grain size)
 |
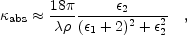(8) |
where 
() =
1 +
i 2
is the complex dielectric function of the grain at wavelength
.
For dielectric spheres,
abs
-1
2
-2 as
since
1
approaches a constant (>>
2)
while 2
-1;
for metallic spheres with a conductivity of
,
abs
-1
2-1
-2
as
since
2 =
2
/ c
and 1
<<
2.
Even for dielectric grains with such an extreme
shape as needle-like prolate spheroids
(of semiaxes l along the symmetry axis
and a perpendicular to the symmetry axis),
in the Rayleigh regime we expect
abs
-2:
 |
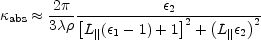(9) |
where
L||
(a / l)2 ln(l / a) is the
depolarization factor parallels to the symmetry axis;
since for dielectric needles
1
constant and
L||(1 - 1) + 1 >> L||
2,
therefore abs
-1
2
-2 (see
Li [36]
for a detailed discussion). Only for both conducting and
extremely-shaped grains
abs can still
be large at very long wavelengths. But even for those grains,
the Kramers-Kronig relation places an upper limit
on the wavelength range over which large
abs
can be attainable (see
Li & Dwek [43]
for details). The Kramers-Kronig relation has also been applied to
interstellar dust models to see if the subsolar interstellar
abundance problem can be solved by fluffy dust
(Li [40])
and to TiC nanoparticles to relate their UV absorption
strength to their quantities in protoplanetary nebulae
(Li [37]).
The inverse-square dependence of
abs on
wavelength derived above applies to both crystalline and amorphous
materials (see
Tielens & Allamandola
[61]
for a detailed
discussion). Exceptions to this are amorphous layered materials
and very small amorphous grains in both of which the phonons are
limited to two dimensions and their phonon spectrum is
thus proportional to the frequency. Therefore, for both
amorphous layered materials and very small amorphous grains
the far-IR opacity is in inverse proportional to wavelength, i.e.
abs
-1
(Seki & Yamamoto [58];
Tielens & Allamandola
[61]).
Indeed, the experimentally measured far-IR absorption
spectrum of amorphous carbon shows a
abs
-1
dependence at 5 µm <
< 340 µm
(Koike, Hasegawa, & Manabe
[29]).
If there is some degree of cross-linking between the layers
in the amorphous layered grains, we would expect
1 < < 2
(Tielens & Allamandola
[61]).
This can explain the experimental far-IR absorption spectra
of layer-lattice silicates which were found to have
1.25 <
< 1.5 at 50 µm <
< 300 µm
(Day [15]).
For very small amorphous grains, if the IR absorption
due to internal bulk modes (for which the density of
states frequency spectrum is proportional to
-2)
is not negligible compared to that due to surface
vibrational modes (for which the frequency spectrum is proportional to
-1),
we would also expect 1 <
< 2
(Seki & Yamamoto [57]).
If there exists a distribution of grain sizes,
ranging from small grains in the Rayleigh regime for which
~ 2 and very
large grains in the geometric optics limit for which
~ 0,
we would expect
to be intermediate between 0 and 2. This can explain the small
values
of dense regions such as molecular cloud cores, protostellar nebulae and
protoplanetary disks where grain growth occurs (e.g. see
Miyake & Nakagawa [50]).
The exponent index
is
temperature-dependent, as measured by
Agladze et al. [1]
for silicates at T = 1.2-30 K and
= 700-2900
µm, and by
Mennella et al. [49]
for silicates and carbon dust at T = 24-295 K and
= 20-2000 µm.
Agladze et al. [1]
found that at T = 1.2-30 K,
first
increases with increasing T, after reaching a maximum at T
~ 10-15 K it starts to decrease with increasing T.
Agladze et al. [1]
attributed this to a two-level population effect
(Bösch [9]):
because of the temperature-dependence of the two-level
density of states (i.e. the variation in temperature results
in the population change between the two levels), the exponent index
is also
temperature dependent. In contrast,
Mennella et al. [49]
found that
increases by ~ 10%-50% from T = 295 K to 24 K,
depending on the grain material (e.g. the variation of
with T for crystalline silicates is not as marked as for
amorphous silicates). The increase of
with decreasing
T at T = 24-295 K is due to the weakening of the long
wavelength absorption as T decreases because at lower
temperatures fewer vibrational modes are activated.
Finally, it is noteworthy that the inverse temperature
dependence of
has been reported by
Dupac et al. [21]
for a variety of regions.