4. OPACITY: ABSOLUTE VALUES

In literature, one of the widely adopted opacities is that of Hildebrand [26]:

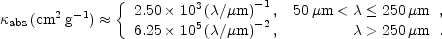(10)

Hildebrand [26] arrived at the above values from first estimating _abs(125 µm) and then assuming 1 for < 250 µm and 2 for > 250 µm. He estimated the 125 µm opacity from _abs(125 µm) = 3Q_abs(125 µm) / (4a ) = 3 / (4a ) [Q_abs(125 µm) / Q_ext(UV)] Q_ext(UV) by taking a = 0.1 µm, = 3 g cm^-3, Q_ext(UV) = 3, and Q_ext(UV) / Q_abs(125 µm) = 4000, where Q_ext(UV) is the ultraviolet extinction efficiency at ~ 0.15-0.30 µm.

The most recent silicate-graphite-PAHs interstellar dust model for the diffuse ISM (Li & Draine [41]) gives

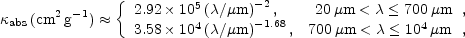(11)

while _abs() 4.6 × 10⁵( / µm)^-2 cm² g^-1 for the classical Draine & Lee [19] silicate-graphite model. The fluffy composite dust model of Mathis & Whiffen [48] has _abs() 2.4 × 10⁵( / µm)^-1.6 cm² g^-1 in the wavelength range of 100 µm < < 1000 µm. The silicate core-carbonaceous mantle dust model of Li & Greenberg [44] gives _abs() 1.8 × 10⁵( / µm)^-2 cm² g^-1 for 30 µm < < 1000 µm. We see that these _abs values differ by over one order-of-magnitude; e.g., the 1350 µm opacity calculated from the composite model [_abs(1350 µm) 2.35 cm² g^-1; Mathis & Whiffen [48]] is higher than that from the silicate-graphite-PAHs model [_abs(1350 µm) 0.20 cm² g^-1; Li & Draine [41]] by a factor of ~ 12.

While the Mathis & Whiffen [48] composite dust model predicts an IR emission spectrum too flat to be consistent with the COBE-FIRAS observational spectrum, and the dust IR emission has not been calculated for the Li & Greenberg [44] core-mantle model which focuses on the near-IR to far-UV extinction and polarization, the silicate-graphite-PAHs model has been shown successful in reproducing the infrared emission spectra observed for the Milky Way (Li & Draine [41]), the Small Magellanic Cloud (Li & Draine [42]), and the ringed Sb galaxy NGC7331 (Regan et al. [57], Smith et al. [60]). Therefore, at this moment the dust opacity calculated from the silicate-graphite-PAHs model is preferred.

It has recently been suggested that the long wavelength opacity can be estimated from the comparison of the visual or near-IR optical depth with the (optically thin) far-IR, submm and mm dust emission measured for the same region with high angular resolution, assuming that both the short wavelength extinction and the long wavelength emission are caused by the same dust (e.g. see Alton et al. [2, 3], Bianchi et al. [5, 6], Cambrésy et al. [12], Kramer et al. [30, 31])

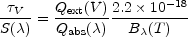(12)

where _V is the visual optical depth, S() is the surface brightness at wavelength , and Q_ext(V) is the extinction efficiency in the V-band ( = 5500Å). With the dust temperature T determined from a modified black-body ^- B(T) fit to the far-IR dust emission spectrum ( is not treated as a free parameter but taken to be a chosen number), Q_abs() can be calculated from the far-IR, submm, or mm surface density S(), and the measured visual optical depth _V [if what is measured is the near-IR color-excess, say E(H - K), instead of _V, one can derive _V from _V 14.6E(H - K)]. In so doing, Q_ext(V) is usually taken to be 1.5.

The long wavelength _abs values recently determined using this method (Eq. [12]) are generally higher than those predicted from the dust models for the diffuse ISM. Although this can be explained by the fact that we are probably looking at dust in dense regions where the dust has accreted an ice mantle and coagulated into fluffy aggregates for which a higher _abs is expected (e.g. see Krügel & Siebenmorgen [34], Pollack et al. [52], Ossenkopf & Henning [51], Henning & Stognienko [25], Li & Lunine [46]), the method itself is subject to large uncertainties: (1) the grains responsible for the visual/near-IR extinction may not be the same as those responsible for the far-IR, submm and mm emission; the latter is more sensitive to large grains while the former is dominated by submicron-sized grains; (2) the dust temperature T may have been underestimated if the actual is larger than chosen; and (3) the fact that in many cases the IRAS (Infrared Astronomical Satellite) 60 µm photometry was included in deriving the dust temperature T results in appreciable uncertainties since the 60 µm emission is dominated by stochastically heated ultrasmall grains; ignoring the temperature distributions of those grains would cause serious errors in estimating the dust mass (see Draine [16]) and therefore also in deriving the long wavelength opacity _abs. These problems could be solved by a detailed radiative transfer treatment of the interaction of the dust with starlight (e.g. Popescu et al. [53], Tuffs et al. [62]) together with a physical interstellar dust model (e.g. the silicate-graphite-PAHs model; see Li & Draine [41, 42]).

Based on the laboratory measurements of the far-IR and mm absorption spectra of both amorphous and crystalline silicates as well as disordered carbon dust as a function of temperature, Agladze et al. [1] and Mennella et al. [49] found that not only the wavelength dependence exponent index but also the absolute values of the absorption are temperature dependent: the far-IR and mm opacity systematically decreases (almost linearly) with decreasing temperature to T ~ 10-15 K and then increases with decreasing temperature at very low temperature. While the linear dependence of _abs on T at T > 10-15 K was interpreted by Mennella et al. [49] in terms of two-phonon difference processes, the inverse-temperature dependence of _abs on T at very low temperature was attributed to a two-level population effect (Agladze et al. [1]). Agladze et al. [1] and Mennella et al. [49] also found that the far-IR and mm opacity of amorphous materials are larger than that of their crystalline counterparts. This is because for amorphous materials, the loss of long-range order of the atomic arrangement leads to a relaxation of the selection rules that govern the excitation of vibrational modes so that all modes are infrared active, while for crystalline solids, only a small number of lattice vibrations are active.