Annu. Rev. Astron. Astrophys. 2003. 41: 191-239 Copyright © 2003 by Annual Reviews. All rights reserved

5. GAS DYNAMICAL EQUATIONS AND CLASSIC COOLING FLOWS

To understand cooling flows at the next level beyond static models, the assumption of steady state flow is often made (Bailey 1980; White & Chevalier 1983, 1984; Nulsen, Stewart & Fabian 1984; Thomas 1986; Sarazin & White 1987; Vedder, Trester & Canizares 1988; Sarazin & Ashe 1989; Tabor & Binney 1993; Bertin & Toniazzo 1995). Although the steady state approximation is useful in gaining insight into various dynamical aspects of subsonic cooling flows, particularly at small galactic radii, inconsistencies can arise if this approximation is applied globally. In particular for subsonic flows there are ambiguities in selecting the boundary conditions near the stagnation radius where the inward integrations begin, as recognized and discussed by Vedder, Trester & Canizares (1988). Steady flows are also incapable of properly allowing for some essential time dependencies such as the strongly decreasing rate of stellar mass loss, variations in the frequencies of Type Ia supernovae, heating by central AGN, and the accretion of intergalactic gas in an evolving cosmology. For these reasons we emphasize non-steady flows in the following discussion.

For galactic scale cooling flows, the usual time-dependent gas dynamical equations must include appropriate source and sink terms:

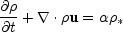(3)

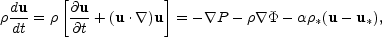(4)

and

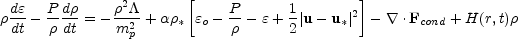(5)

where = 3kT / 2 µ m_p is the specific thermal energy. The gravitational potential in the momentum Equation (4) includes contributions from both stellar and dark mass; the mass of hot gas is usually negligible. The coefficient = _* + _sn is the specific rate of mass loss from the stars and Type Ia supernovae, i.e. M_*t 0.15 M_*t / (10¹¹ M) M yr^-1 is the total current rate of mass loss from evolving stars in NGC 4472. Because _sn is much less than _*, _* is an excellent approximation. The specific mass loss rate from a single burst stellar population with Salpeter IMF and age t varies as _*(t) = 4.7 × 10^-20(t / t_n)^-1.3 s^-1 where t_n = 13 Gyrs (Mathews 1989); for other powerlaw IMFs _*(t_n) varies inversely with the stellar mass to light ratio.

A fundamental assumption is that gas ejected from evolving giant stars as winds or planetary nebulae eventually becomes part of the hot phase. The interaction of gas ejected from orbiting stars with the hot galactic gas is extremely complicated, involving complex hydrodynamic instabilities that enormously increase the surface area between the ejected gas and its hot environment until, as usually assumed, the two gases thermally fuse. As we discuss below, the positive temperature gradients observed in inner cooling flows of cluster-centered elliptical galaxies and the hot gas oxygen abundance gradients provide indirect evidence that such mixing does occur. The term _* (u - u_*) in Equation (4) represents a drag on the flow, assuming gas expelled from stars has on average the mean stellar velocity u_*, which is non-zero only in rotating galaxies. This drag term is generally negligible if the flow is subsonic. If u_* = 0, this term has the effect of making subsonic flow even more subsonic and supersonic flow even more supersonic.

The thermal energy Equation (5) contains a term - ( / m_p)² (T, z) for the loss of energy by X-ray emission; the radiative cooling coefficient (T, z) erg cm³ s^-1 varies with both gas temperature and metal abundance (e.g. Sutherland & Dopita 1993). The dissipative heating _{* *} |u - u_*|² / 2 involved in accelerating stellar ejecta to the local flow velocity is usually very small. The hot gas temperature is also influenced by stellar mass loss and Type Ia supernovae. The source terms _{* *} (_o - P / - ) represent the heating of the hot interstellar gas of specific energy by the mean energy of stellar ejecta _o less the work done P / in displacing the hot gas. The mean gas injection energy is _o = 3k T_o / 2 µ m_p where T_o = (_* T_* + _sn T_sn) / . The stellar temperature T_* can be found by solving the Jeans equation, but this term is small and it is often sufficient to use an isothermal approximation, T_* = ( µ m_p / k)², where is the average stellar velocity dispersion. Supernova heating is assumed to be distributed smoothly in the gas, ignoring the detailed evolution of individual blast waves (Mathews 1990). The heating by Type Ia supernovae, each of energy E_sn 10⁵¹ ergs, is described by multiplying the characteristic temperature of the mass M_sn ejected, T_sn = 2 µ m_p E_sn / 3k M_sn, by the specific mass loss rate from supernovae, _sn = 3.17 × 10^-20 SNu(t)(M_sn / M) _B^-1 s^-1. Here the supernova rate SNu is expressed in the usual SNu-units, the number of supernovae in 100 yrs expected from stars of total luminosity 10¹⁰ L_B .

Supernovae in ellipticals today are infrequent and all of Type Ia. Cappellaro et al. (1999) find SNu(t_n) = (0.16 ± 0.05) h₇₀² for E+S0 galaxies. The past evolution of this rate SNu(t) is unknown, although some provisional data is beginning to emerge (Gal-Yam, Maoz, & Sharon 2002). Clearly, it would be very useful to have more information about SNu(t) for E galaxies at high redshift because this can have a decisive influence on the evolution of the hot gas and its iron abundance. Type Ia supernovae may involve mass exchange between binary stars of intermediate mass, but the details are very uncertain (e.g. Hillebrandt et al. 2000). However, like all cosmic phenomena, it is generally assumed that SNu(t) is a decreasing function of time, SNu(t) = SNu(t_n)(t / t_n)^-s. This is consistent with measurements at intermediate redshifts if s ~ 1 (Pain et al. 2002), although these observations refer to all galaxy types.

Ciotti et al. (1991) recognized that the relative rates of stellar mass ejection (_* ~ t^-1.3) and Type Ia supernova (SNu ~ t^-s) determine the dynamical history of the hot interstellar gas in ellipticals. For example, if s > 1.3 in isolated ellipticals then the supernova energy per unit mass of gas expelled from stars ( _sn / _*) was large in the distant past, promoting early galactic winds, but if s < 1.3, outflows or winds tend to develop at late times. However, in the presence of circumgalactic gas, the early time galactic winds driven by Type Ia supernovae can be suppressed. Each Type Ia supernova injects ~ 0.7 M of iron into the hot gas, producing a negative iron abundance gradient in the hot gas that depends on _* / and the radial flow velocity of the gas. The observed SNIa enrichment provides an important constraint on dSNu(t) / dt (Loewenstein & Mathews 1991). Evolutionary flow solutions with s > 1.3 produce iron abundances far in excess of those observed today, unless the iron is preferentially removed by selective cooling. We therefore have tentatively adopted s = 1 with SNu(t_n) = 0.06 SNu (similar to the estimate of Kobayashi et al 2000) although this is by no means the only possibility. This adopted current Type Ia supernova rate is less than the rate observed in E plus S0 galaxies, but the rate may be lower for ellipticals than for S0 galaxies.

Thermal conductivity in a hot plasma, 5.36 × 10^-7 T^5/2 erg s^-1 cm^-1 K^-1 is important at high temperatures, but may be reduced by tangled magnetic fields. The conductive energy flux in Equation (5), F_cond = f dT / dr, usually includes an additional factor f 1 to account for magnetic suppression. In the past f << 1 has often been assumed, but Narayan & Medvedev (2001) have recently shown that f ~ 0.2 is appropriate for thermal conduction in a hot plasma with chaotic magnetic field fluctuations. The final term in Equation (5), H(r, t) , is an ad hoc AGN heating term that is discussed later.

Using the relation _* 8.54 × 10^-20 n_e² from Figure 2a, we find at the current time t_n that ( / m_p)² is about an order of magnitude greater than _{* *}(_o - P / - ). For galactic flows with T ~ 10⁷ K thermal conduction is important for f 0.5. Therefore, if dissipation and AGN heating are small in NGC 4472, ( / m_p)² dominates all other non-adiabatic terms in Equation (5), generating a classic cooling inflow driven by radiative losses. As radiative energy is lost in a Lagrangian frame moving with the gas, the entropy decreases, but the gas temperature ~ T_vir remains relatively constant as the gas is heated in the gravitational potential by Pdv compression. The compression drives gas slowly toward the galactic center where, in this simple example, Pdv heating is no longer available and catastrophic cooling ensues. Because of this self-regulating mechanism, the temperature profile T(r) in cooling flows is very insensitive to modest changes in the source terms in the thermal energy Equation (5), including ( / m_p)² .

To gain further insight, it is instructive to insert the observed gas density and temperature profiles for NGC 4472 into Equations (3) and (5) and estimate the steady state radial gas velocity, assuming _* is fixed at its current value. For a steady inflow Equation (3) can be integrated from r to and solved for the flow velocity, u(r) = {() - _*[M_*t - M_*(r)]} / 4 r² . This is the negative velocity required to continuously remove mass supplied by mass-losing galactic stars without changing (r). Assuming () 0 and using NGC 4472 parameters, we find u(r) - 51 r_kpc^-1.05 km s^-1 for 0.25 r_kpc 10; at larger r in NGC 4472 the inflow of circumgalactic gas () < 0 must be considered but for r R_e = 8.57 kpc we can assume the mass lost from the stars determines (r). Another steady state velocity can be found by inserting the observed (r) and T(r) (Fig. 2) into the first three terms of Equation (5),

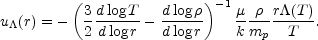(6)

This "slump" velocity in NGC 4472, u(r) -27r_kpc^-0.36 km s^-1 for 0.3 r_kpc 40, is the inflow that occurs because gas is cooling near the center and occupying less volume. Both u and u are very small compared to the adiabatic sound speed in the hot gas, 476(T / 10⁷ K)^1/2 km s^-1, so either type of flow satisfies the requirement for hydrostatic equilibrium. However, for r_kpc 2.5, |u| > |u|, i.e., the inflow required to conserve the observed gas density profile exceeds the rate that the gas can cool, violating the assumption of steady flow. Consequently, if the observed (r) and T(r) are taken as initial conditions in a time-dependent gasdynamical calculation for NGC 4472, subsonic inflowing solutions evolve toward higher gas densities near the origin, increasing the radiative losses there until u(r) u(r). This explains why the central gas density exceeds observed values in every otherwise successful steady state or time-dependent inflow model without central AGN heating or thermal conduction.