Annu. Rev. Astron. Astrophys. 2005. 43: 861-918 Copyright © 2005 by Annual Reviews. All rights reserved

2. THE NEUTRAL-GAS CONTENT OF THE UNIVERSE

In this section we describe how the surveys allow us to measure _g(z), the mass per unit comoving volume of neutral gas in damped Ly systems at redshift z divided by the critical density, _crit. The results, first derived by Wolfe (1986) and Lanzetta, Wolfe & Turnshek (1995) show that damped Ly systems contain most of the neutral gas in the Universe at redshifts 1.6 < z < 5.0.

2.1. Formalism

To estimate _g(z) we first derive an expression for the column-density distribution, f(N, X). Let the number of absorbers per sightline with H I column densities and redshifts in the intervals (N, N + dN) and (z, z + dz) be given by

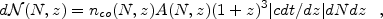(1)

where n_co(N, z)dN is the comoving density of absorbers within (N, N + dN) at z and A(N, z) is the absorption cross-section at (N, z). Defining dX (H₀ / c)(1 + z)³ |c dt / dz| dz (Bahcall & Peebles 1969) we have

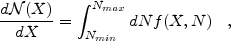(2)

where

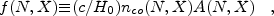(3)

and N_min and N_max are minimum and maximum column densities, respectively. ¹ Therefore, one cannot infer the comoving density nor the area of damped Ly systems from their incidence along the line of sight, but only their product. Note that d / dX will be independent of redshift if the product of the comoving density and absorption cross-section at (N, X) is independent of redshift. Since the gaseous mass per damped Ly system is given by µ m_HNA(N,X), it follows from Equation 3 that

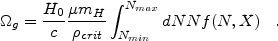(4)

where µ is the mean molecular weight, which is included to account for the contribution of He to the neutral gas content.

Using these expressions in the discrete limit, several authors have determined f(N, X) and its first two moments, d / dX and _g(z), where

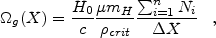(5)

and n is the number of damped Ly systems within (X, X + X). We now discuss each of these in turn.

2.2. f(N, X)

Figure 3 shows the most recent determination of f(N, X) from the statistical sample of over 600 damped Ly systems (Prochaska, Herbert-Fort & Wolfe 2005). The figure also shows best-fit solutions for the three functional forms used to describe f(N, X): a single power-law, f(N, X) = k₁ N^₁; a function (e.g., Pei & Fall 1993) f(N, X) = k₂(N / N)^₂ exp(-N / N); and a double power-law f(N, X) = k₃(N / N) where = ₃ at N < N_d and ₄ at N N_d. The single power-law solution with a best-fit slope of ₁ = -2.20 ± 0.05 is a poor description of the data since a KS test shows there is a 0.1% probability that the data and power-law solution are drawn from the same parent population. This result is in contrast with the Ly forest where a single power-law with ₁ -1.5 provies a good fit to the data (Kirkman & Tytler 1997).

Although a single power-law is a poor fit to the observations, the f(N, X) distribution is steeper than N^-2 at large column densities. This is illustrated by the other two curves in Figure 3 that show the function (dashed line) and the double power-law (dashed-dot line). Both solutions are good fits to the data. Furthermore, the solutions provide good agreement between the "break" column densities N and N_d, and between the power-law indices at low column densities, which approach a "low-end" slope = -2.0. Most importantly, both solutions indicate << - 2.0 at N 10^21.5 cm^-2. The significance of this very steep slope at the "high end" will be explored further in Section 2.4.

Prochaska, Herbert-Fort & Wolfe (2005) also find evidence for evolution in f(N, X), which will be clearly visible in the redshift dependence of d / dX, the zeroth moment of f(N, X), and of _g(z), the first moment of f(N, X) (see Sections 2.3 and 2.4). At low column densities, f(N, X) increases with redshift by a factor of 2 at z 2.2. Prochaska, Herbert-Fort & Wolfe (2005) detect a similar evolution at higher values of N. By contrast, the shape of f(N, X) does not appear to evolve with redshift. This is in disagreement with the earlier results of Storrie-Lombardi & Wolfe (2000) and Péroux et al. (2003b) who used much smaller samples to claim that f(N, X) steepened at z > 3.5.

2.3. d / dX

In Figure 4 we plot the most recent evaluation of d / dX versus z for damped Ly systems with z 0 (see Prochaska, Herbert-Fort & Wolfe 2005). The solid line traces the value of d / dX derived in a series of 0.5 Gyr time intervals to reveal the effects of binning. The data points at z = 0 are three estimates of (d / dX)_z=0 based on the H I properties of nearby galaxies. The figure shows a decrease by a factor of two in d / dX from z = 4 to 2. From Equations 2 and 3 we see that the decrease in d / dX reflects a decrease in either H I cross section, comoving density, or of both quantities. Prochaska, Herbert-Fort & Wolfe (2005) use the Press-Schecter formalism to show that significant variations in comoving density with time are unlikely to occur. Therefore, within the context of CDM models the most likely explanation for the changes in d / dX is a decrease in H I cross section with time. This is probably due to feedback mechanisms such as galactic winds.

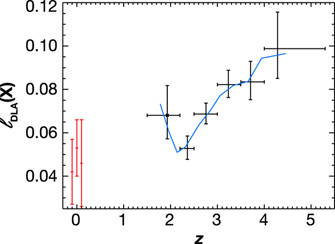Figure 4. Incidence of damped Ly systems per unit cosmological distance d / dX (denoted as c in the figure) as a function of redshift. The three data points at z = 0 are all local measurements from 21 cm observations (Rosenberg & Schneider 2003; Ryan-Weber, Webster & Staveley-Smith 2003; Zwaan et al. 2001). The curve overplotted on the data traces the evaluation of d / dX in a series of O.S Gyr intervals. Plot taken from Procheska, Herbert-Fort & Wolfe (2005).

Figure 4 also shows that d / dX at z 2 is consistent with the present-day value, i.e., the data are consistent with an unevolving population of galaxies. ² By comparison, Wolfe et al. (1986) required an increase of more than a factor of 4 with redshift in d / dX. The discrepancy arises from the earlier use of an Einstein-deSitter rather than the modern CDM cosmology to estimate X intervals, and from the lower values of (d / dX)_z=0 used in the earlier work. This result implies that between z = 1 and 2 smaller galaxies merged to produce bigger ones such that the product of comoving density and total H I cross-section for N(H I) 2 × 10²⁰ cm^-2 is conserved.

2.4. _g(z)

Figure 5 shows the most recent determination of _g(z). From Equation 4 we see that _g(z) is sensitive to the upper limit N_max unless << -2. This led to large uncertainties in _g(z) in previous work because was not measured with sufficient accuracy to rule out -2. However, with the large sample of over 600 damped Ly systems, Prochaska, Herbert-Fort & Wolfe (2005) use several tests to show that _g(z) converges. First, they compute ₁ for a single power-law fit to f(N, X) by increasing N_min from 2 × 10²⁰ cm^-2. Using the full sample of damped Ly systems they find ₁ decreases with increasing N_min from -2.2 at N_min = 2 × 10²⁰ cm^-2 to less than -3 at N_min > 10²¹cm^-2. At the same time they find that ₁ is insensitive to variations in N_max. Second, they compute the sensitivity of _g(z) to N_max. Both the double power-law and function solutions converge to the value indicated by the data (Equation 5). By contrast the single power-law solution does not converge. This is the first evidence that _g(z) converges by N 10²² cm^-2.

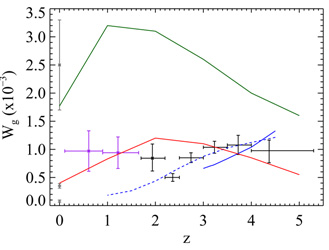Figure 5. Neutral gas mass density versus z from Prochaska et al. (2005). H I data at (a) z 2.2 from SDSS-DR3_4 survey, (b) 0 < z < 1.6 from the MgII survey of S.M. Rao, D.A. Turnshek & D.B. Nestor (private communication), and (c) at z = 0 (red diamond) from Fukugita et al. (1998). Stellar mass density at z = 0 (red star) from Cole et al. (2001) and stellar mass density of Irr galaxies (red plus sign) from Fukugita et al. (1998). Theoretical curves from Cen et al. (2003) (green), Somerville et al. (2001) (yellow), and Nagamine et al. (2004a) (blue; dotted is D5 model and solid is Q5 model).

Next, consider the redshift evolution of _g(z). Starting at the highest redshifts, no increase of _g(z) with decreasing z is present at z > 3.5, contrary to earlier claims (Storrie-Lombardi & Wolfe 2000, Péroux et al. 2003b). On the other hand, Figure 5 shows the first statistically significant evidence that _g(z) evolves with redshift. Specifically, _g(z) decreases from 1 × 10^-3 at z = 3.5 to 0.5 × 10^-3 at z = 2.3, which mirrors the decline in d / dX discussed in Section 2.3. The same mechanism is likely to cause the decline in both quantities, i.e., a decrease in H I cross section due to feedback. But at z < 2.3 the picture is somewhat confusing. Figure 5 shows an increase of _g(z) by z ~ 2, which is consistent with the values of _g(z) in the two lower redshift bins at 0 < z < 2. Indeed, the data are consistent with no evolution, if one ignores the redshift interval centered at z = 2.3. However, Prochaska, Herbert-Fort and Wolfe (2005) emphasize that the uncertainties in the data at 0 < z < 2.3 are much larger than at z > 2.3, and thus such conclusions should be treated with caution.

Next, we compare the high-z values of _g(z) with various mass densities at z = 0. First, comparison with the current density of visible stars, _*, reveals that _g(z) at z 3.5 is a factor of 2 to 3 lower than _*: If the census of visible stars were restricted to stellar disks, then _g(z) at these redshifts would exceed _* (z = 0). A straightforward interpretation of this concurrence is that damped Ly systems provide the neutral gas reservoirs for star formation at high redshifts. However, since _* (z = 0) exceeds _g(z 3.5), the reservoir must be replenished with new neutral gas before the present epoch. Further evidence for replenishment is that it is required to compensate for gas depletion due to star formation detected in damped Ly systems (see Section 8). As a result, the "closed box" hypothesis for evolution in damped Ly systems is unlikely to be correct (see Lanzetta et al. 1995).

Figure 5 also shows that _g(z) at z 3.5 is significantly higher than _g(z) at z = 0, which is deduced from surveys for 21-cm emission. Therefore, damped Ly systems provide direct evidence for the widely held theoretical view that the neutral gas content of the universe was larger at high redshifts than it is today. Figure 5 also shows that _g(z) at z 3.5 is at least a factor of 10 greater than _* in dwarf irregular galaxies, which argues against the idea that damped Ly systems evolve into such objects (e.g., Jimenez et al. 1999).

Therefore, since Lyman limit systems do not contribute significantly to the neutral gas content at any redshift (see Prochaska, Herbert-Fort & Wolfe 2005) and ignoring the possible existence of a significant population of dusty giant molecular clouds, we conclude that damped Ly systems contain most of the gas available for star formation at z 1.6. At low redshifts the ionizing background is reduced and lower N(H I) systems might be mainly neutral. But at z = 0, Minchin et al. (2003) find a paucity of galaxies with column densities less than N(H I) = 2 × 10²⁰ cm^-2 measured from 21 cm emission, implying that at the lowest redshifts, damped Ly system column densities comprise most of the neutral gas in the universe. As a result, damped Ly systems dominate the neutral-gas content of the universe in the redshift interval 0 < z < 5.

Of course, all of these conclusions ignore obscuration by dust in damped Ly systems, which may have biased the form of f(N, X) (see Pei, Fall & Bechtold 1991; Fall & Pei 1993). We discuss this possibility in Section 10. They also ignore biassing due to lensing, which may be present (see Section 12).

2.5. Model Comparisons

Here we discuss attempts to use the H I content of damped Ly systems to test models of galaxy formation and evolution.

2.5.1. PASSIVE EVOLUTION: THE NULL HYPOTHESIS

Boissier, Péroux & Pettini (2003) modeled the evolution of H I content within the null hypothesis of passive evolution. In this scenario damped Ly absorption arises in disk galaxies with the comoving density of current spiral galaxies. The models are hybrids of passive evolution, in which the H I content is changed only by processes of stellar evolution, and the spherical collapse model in an expanding Universe, in which high-z disks are smaller than current disks. The models successfully explain the measurement of d / dX, f(N, X), and _g(z) at z < 2 but fall short at higher redshifts because of delayed disk formation. For these reasons, the authors suggest the added presence of a population of low-surface brightness, gas-rich galaxies at z 2. However, evidence against the "closed box" hypothesis discussed in Section 2.4 is a difficult challenge for this and all passive evolution models.

2.5.2. NUMERICAL SIMULATIONS

Several aspects of cosmology and galaxy formation have been examined through comparisons of numerical simulations of galaxy formation in a CDM Universe with the observed H I properties of damped Ly systems. A critical feature of these models is that gas falling onto dark-matter halos is heated to their virial temperatures, then cools off, and collapses toward the central regions of the halos. Galaxies arise from the formation of stars out of the cool (presumably neutral) collapsed gas and evolve through mergers between dark-matter halos and further infall of gas onto the halos.

The first studies (Klypin et al. 1995, Ma & Bertschinger 1994) constrained the cosmological mass constituents through comparisons with _g(z). The observations severely restricted the contribution from a hot component (i.e., neutrinos) as these cold + hot dark matter cosmogonies underpredicted structure formation at early times (Katz et al. 1996). Subsequent papers by Gardner et al. (1997a, b, 2001) examined the properties of damped Ly systems in their smooth particle hydrodynamic (SPH) simulations. These models generically underpredicted the incidence of damped Ly systems, which the authors argued was due to an insufficient mass resolution of 10¹¹ M. They did find reasonable agreement with the data, however, by extrapolating to halos with M_h 10¹⁰ M using the Press-Schechter formalism, and by assuming that the H I cross-section followed the power-law expression A v_c^1.6. As stressed by Prochaska & Wolfe (2001), this power-law expression implies a v_c distribution that is incompatible with the observed damped Ly velocity widths (see Section 6).

Nagamine, Springel & Hernquist (2004a) recently analyzed a comprehensive set of high-resolution SPH simulations of a CDM Universe. By contrast with Gardner et al. (1997a), they find that halo masses down to M_h 10⁸ M contribute to the H I cross-sections: halos with M_h < 10⁸ M do not contribute since they contain only photo-ionized gas. In turn, Nagamine et al. find a steeper power-law expression A v^2.7_c, i.e., massive halos make a larger contribution to d / dX than in previous models. They conclude that Gardner et al. (1997a) predicted an overabundance of damped Ly systems with M_h < 10¹⁰ M because the slope of their A versus v_c relation was too shallow. Nagamine, Springel & Hernquist (2004a) were the first to include mass loss of neutral gas due to winds, which increases the median halo-mass contribution to d / dX to 10¹¹ M. Winds also prevent an overabundance of _g(z) at z 4, but underpredict _g(z) at z < 4. Nagamine, Springel & Hernquist (2004a) continue to find a deficit of damped Ly systems with N(H I) < 10²¹cm^-2. The deficit of systems with low N(H I) is a generic effect seen in most (e.g., Figure 3 in Katz et al. 1996) but not all numerical simulations (Cen et al. 2003) and is a shortcoming that needs to be addressed. On the other hand, the Nagamine, Springel & Hernquist (2004a) models are the most successful in reproducing the evolution of _g(z) at z 2 (Figure 5).

2.5.3. SEMIANALYTIC AND ANALYTIC MODELS

The semianalytic models were proposed to include processes beneath the resolution of the numerical simulations with phenomenological descriptions of star formation, gas cooling, and the spatial distribution of the gas. The latter is included since the simulations failed to reproduce the correct sizes and angular momenta of present-day galactic disks (Navarro & Steinmetz 2000), and we do not know whether the simulations produce the correct spatial distribution of neutral gas at z ~ 3. This is a concern because damped Ly systems are a cross-section weighted population of high-redshift layers of neutral gas and therefore the results will be sensitive to the gas distribution at large impact parameters. By contrast with the numerical simulations, one uses analytic expressions from Press-Schechter theory or its extensions (Press & Schechter 1974; Sheth, Mo & Tormen 2001) to compute the mass function of halos that evolve from a given power spectrum.

Mo & Miralda-Escudé (1994) modeled damped Ly systems with the Press-Schechter formalism in both mixed cold + hot dark matter and CDM cosmologies. Kauffmann (1996) used a SCDM cosmology ([_M, , h] = 1.0, 0.0, 0.5) to construct improved semianalytic models for damped Ly systems. She assumed spherical geometry for the halos and let the neutral-gas in a given halo be confined to a smaller, centrifugally supported disk. To compute the radial distribution of the neutral gas, the angular momentum per unit mass of the disk was set equal to that of the halo. Using Monte Carlo methods, she computed the formation and growth of individual halos with time. The neutral-gas content was assumed to be regulated by accretion due to mergers and star formation, but feedback due to winds was omitted. In common with the Nagamine, Springel & Hernquist (2004a) simulations, the Kauffmann (1996) models exhibited a deficit of systems with N(H I) < 10²¹cm^-2.

Mo, Mao & White (1998) constructed models for disk formation that were also based on the Press-Schechter formalism. These models extended the work of Kauffmann (1996) by considering disks drawn from a distribution of halo spin parameters, _H, rather than using Kauffmann's technique of assigning the mean value of _H to each disk. Since disks detected in a survey for damped Ly systems are drawn from a cross-section weighted sample favoring bigger disks, the distribution of _H will be skewed to values higher than the unweighted mean. The result is larger H I cross-sections and higher detected rotation speeds. Consequently, they found agreement between the predicted and observed d / dX relation. Maller et al. (2001) then suggested a model in which the gas is in extended Mestel (1963) disks in which the surface density falls off inversely with the radius. In this case the disks overlap and as a result the observed f(N, X) is reproduced; i.e., there is no deficit of systems with N(H I) < 10²¹cm^-2. However, it is unclear whether such extended disks will either form or survive sufficiently long to contribute to the H I cross-sections of damped Ly systems. Furthermore, most semianalytic models overestimate _g(z) at z 2, since they underpredict feedback processes at these redshifts (Figure 5).

¹ Note that dX / dz = (1 + z)²[(1 + z)²(1 + z _m) - z(z + 2) ]^-1/2 Back.

² Ryan-Weber et al.(2003) present evidence that f (N, X) at z = 0 is significantly lower in amplitude than the results at higher redshifts, but this result is puzzling since comparison between the resultant d / dX at z = 0 with the higher redshift data in Figure 4 reveals no evidence for evolution. Back.