Annu. Rev. Astron. Astrophys. 2005. 43: 861-918 Copyright © 2005 by Annual Reviews. All rights reserved

3. CHEMICAL ABUNDANCES

Because the damped Ly systems comprise the neutral gas reservoir for star formation at high redshifts, a determination of their metal content is a crucial step for understanding the chemical evolution of galaxies. Therefore, the mass of metals per unit comoving volume that they contribute indicates the level to which the neutral gas reservoir has been chemically enriched. Since the metal abundances of damped Ly systems have been determined in the redshift interval z = [0, 5], it is now possible to track the chemical evolution of the reservoir back 10 Gyr to the time the thin disk of the galaxy formed (z = 1.8 for the WMAP cosmological parameters adopted here), and to earlier epochs. As a result, one can construct an "age-metallicity" relation not just for the solar neighborhood (see Edvardsson et al. 1993) but for a fair sample of galaxies in the Universe.

In this section we describe the main results that have emerged from abundance studies of damped Ly systems. This subject has also recently been reviewed in an excellent article by Pettini (2004).

3.1. Methodology

The element abundances of the damped Ly systems are the most accurate measurements of chemical enrichment of gas in the high-redshift Universe. The measurements are accurate for several reasons: (1) For the majority of damped Ly systems, hydrogen is mostly neutral, i.e., H⁰/H = 1, and most of the abundant elements are singly ionized, though a minority are neutral, i.e., Fe⁺/Fe = Si⁺/Si = 1, etc., while O⁰/O = N⁰/N = 1. The singly ionized elements have ionization potentials of their neutral states that are lower than the ionization potential of hydrogen, IP(H) (= 13.6 eV). With Lyman limit optical depths, _LL >> 10³, damped Ly systems are optically thick at photon energies, IP(H) < h < 400 eV. As a result, only photons with h < IP(H) and h 400 eV penetrate deep into the neutral gas. When FUV photons with h < IP(H) penetrate, they photoionize the neutral state of each element to the singly ionized state. But this state is shielded from photons with IP(H) < h < 400 eV, which would otherwise photoionize the elements to higher states. Photons with h > 400 eV will produce species that are doubly ionized (e.g., Fe²⁺ and Al²⁺) and singly ionized (e.g., Ar⁺), but because the photoionization cross-sections are low at such high photon energies, the ionization rates are low. It is possible to detect all of these species because they exhibit resonance transitions that are redshifted to optical wavelengths accessible with ground-based spectrographs. (2) In Section 1 we saw that Voigt fits to the damped Ly profiles result in typical errors of 0.1 dex in N(H I). As we shall see, the errors in the column densities which give rise to the narrow low-ion lines are typically 0.05 dex. Consequently, errors in [X/H] are relatively low (typically about 0.1 dex).³ (3) Column densities are straightforward to measure from resonance lines, since their optical depths are independent of poorly determined physical parameters such as the density and temperature of the absorbing gas.

By contrast, abundance determinations for the other constituents of the high-redshift Universe are more uncertain primarily because the gas is ionized. As a result, the abundances are subject to ionization corrections that depend on uncertainties in the spectral shape of the ionizing continuum radiation and on the transport of such radiation. Furthermore, the strengths of QSO emission lines depend on the temperature and density of the emitting gas as well as uncertain photon escape probabilities in the case of resonance scattering. Typical error estimates are about 50% per object, which is several times higher than for damped Ly systems (see Hamann & Ferland 1999 for an excellent review of this subject).

Figure 6 shows examples of absorption profiles obtainable with the HIRES Echelle spectrograph mounted on the Keck I 10-m telescope. The figure shows velocity profiles for abundant low ions in two damped Ly systems. As in most damped Ly systems the gas that gives rise to low-ion absorption lines in these two objects comprises multiple discrete velocity structures of enhanced density, i.e., clouds. To infer the ionic column densities required for element abundance determinations, one integrates the "apparent optical depth" (Jenkins 1996, Savage & Sembach 1991) over the velocity profile.

Figure 6. Velocity profiles of metal-line transitions for (a) the metal-poor damped Ly system at z = 3.608 toward Q1108 - 07 and (b) the metal-strong damped Ly system at z = 2.626 toward Q0812 + 32. Gray indicates the range of flux between 0 and 1. Red lines are blends due to other transitions.

To illustrate the essentials of abundance determinations we focus on two damped Ly systems, one metal-poor (DLA1108-07 at z = 3.608) and the other metal-rich (DLA0812 + 32 at z = 2.626). ⁴ The corresponding velocity profiles in Figure 6 describe the challenges as well as the advantages of measuring damped Ly abundances. First, consider the challenges. The abundance of carbon has not been accurately determined for any damped Ly system because the only resonance transition outside the Ly forest, C II 1334.5, is not only saturated in the metal-rich system (Figure 6b), but also saturated in the metal-poor system (Figure 6a). The availability of several O I transitions makes it possible to place bounds on the oxygen abundance. Several authors used saturated O I 1302.1 to obtain lower limits and the weaker O I 971.1 or O I 950.8 transitions for upper limits since the latter transitions are usually blended with Ly forest absorption features (Dessauges-Zavadsky, Prochaska & D'Odorico 2002; D'Odorico & Molaro 2004; Molaro et al. 2000). On the other hand, a direct determination of [O/H] is possible for the metal-rich system shown in Figure 6b because this is the only known case in which an unsaturated transition, O I 1355.6, is detected.

Second, consider the advantages. Abundance determinations are possible for Fe, Si, and S because of the presence of transitions with a wide range of oscillator strengths. In the case of Fe, the oscillator strengths f_1611.2 = 0.00136 for Fe II 1611.2 and f_1608.4 = 0.0580 for Fe II 1608.4. Thus, in the metal-poor damped Ly system in Figure 6a Fe II 1611.2 is undetected, while unsaturated Fe II 1608.4 is detected. By contrast, in the metal-rich damped Ly system in Figure 6b unsaturated Fe II 1611.2 is detected, while Fe II 1608.4 is saturated. In both systems the iron abundance is determined from the unsaturated transitions. Similarly, Figure 6 also demonstrates how the Si II 1304.3, 1808.0 pair of transitions determines the silicon abundance for the two damped Ly systems.

3.2. Metallicity

Whereas the abundance ratios discussed above refer only to elements in the gas phase, some fraction of each element could be depleted onto dust grains, as in the Galaxy ISM (Jenkins 1987). Meyer, Welty & York (1989) and Pettini, Boksenberg & Hunstead (1990) recognized this possibility early on and made use of the Zn II 2026.1, 2062.6 doublet to measure the metallicities of damped Ly systems. Zn is well suited for this purpose because it is relatively undepleted in the Galaxy ISM with a mean depletion of [Zn/H] -0.23 (Savage & Sembach 1996). Moreover, Zn was believed to be an accurate tracer of Fe peak elements since [Zn/Fe] 0 for stars with metallicities -2.0 < [Fe/H] < 0 (but see the discussion below). In addition, the combination of the low solar abundance of Zn and the oscillator strengths of the Zn II transitions implies that they should be unsaturated for N(H I) < 10²¹cm^-2, provided the velocity dispersion of the gas, _v 4 km s^-1. Because of its proximity in wavelength, the Cr II 2056.2, 2062.2, 2066.1 triplet was used to study depletion, since most of the Cr in the Galaxy ISM is locked up in grains (Jenkins 1987).

In subsequent surveys on several 4-m class telescopes, Pettini and colleagues (Pettini et al. 1994a, 1997b, 1999) increased the size of their sample and confirmed that damped Ly systems are metal poor in the redshift interval z = [0.5, 3.0]. Pettini (2004) found that the cosmic metallicity < Z> = -1.11 ± 0.38, where < Z> is defined as the log of the ratio of the comoving densities of metals and gas, _metals / _g, relative to the solar abundance, i.e., from Equation 5

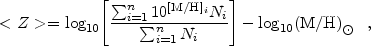(6)

where M stands for the metallicity indicator, which in this case is Zn. Second, surprisingly, there is no positive evidence for redshift evolution. Specifically, Pettini (2004) finds no statistically significant evidence for redshift evolution in < Z>. This is contrary to most models of chemical evolution (see Section 9), which predict an increase in the mean Zn abundance with decreasing redshift, and further predict that the metallicity should approach < Z> = 0, by the current epoch. The sub-solar values of < Z> at z < 1 raised the possibility that damped Ly systems do not evolve into normal current galaxies (Pettini et al. 1999).

Further progress was achieved with the completion of a larger survey of over 120 damped Ly systems carried out primarily on the Keck 10-m telescopes (Prochaska et al. 2003a). In this survey most of the metallicities, [M/H], are obtained from measurements of -enhanced elements Si, S, and O in order of decreasing priority and in a few cases from Zn. Like Zn, S and O are volatile elements that are essentially undepleted in the Galaxy ISM. While the refractory element Si is depleted in the Galaxy ISM, it is only mildly depleted in damped Ly systems, where Si tracks S, i.e., [Si/S] > -0.1 (Prochaska & Wolfe 2002), and thus can generally be used as an unbiased metallicity tracer. Furthermore, since S and Si have higher solar abundances than Zn, they can be used to probe down to metallicities below the Zn threshold of [Zn/H] -1.7. In addition, the shorter wavelengths of crucial transitions such as S II 1250.5 and Si II 1304.3 allow one to obtain metal abundances at higher redshifts than are accessible with the Zn II transitions alone. Note that the idea of combining abundances of Zn and -enhanced elements is plausible if Zn is a tracer of elements such as S and Si. The recent finding by Prochaska & Wolfe (2002) that [Si/Zn] = 0.03 ± 0.05 supports this hypothesis. Further support comes from the finding that [Zn/Fe] ranges between 0.10 and 0.20 (Bihain et al. 2004, Nissen et al. 2004, Prochaska et al. 2000) in stars with [Zn/H] -1.5, which indicates that Zn is not a strict tracer of Fe peak elements. In fact, there is currently little reason to expect [Zn/Fe] = 0 apart from a coincidence related to the star-formation history of the Galaxy (Fenner, Prochaska & Gibson 2004).

The results of Prochaska et al. (2003a) are shown in Figure 7 (updated to include new data at z < 1.5 from Kulkarni et al. 2004 and Rao et al. 2004). The new survey confirms the low metallicities of damped Ly systems found by Pettini and colleagues. However, the greater accuracy and larger redshift range of the new survey allow one to draw additional conclusions. First, there are no damped Ly systems with [M/H] < -2.6. This limit is robust because there are no damped Ly systems without significant metal absorption. Second, Prochaska et al. (2003a) find statistically significant evidence for a linear increase of < Z > with decreasing z. This result is robust owing to the large value of _i^m N_i. This is important since the shape of f(N, X) indicates that < Z > is sensitive to the metallicity of systems with the largest values of N(H I). Because _i^m N_i 1 × 10²² cm^-2 in each of the high-redshift bins, only unusual, very metal-rich systems with N(H I) > 10²² cm^-2 could increase < Z > significantly, i.e., only systems which depart significantly from the current N(H I) versus [M/H] relation could cause a marked increase in < Z >. Earlier claims for evolution had statistical significance lower than 3 and sampled lower values of _iⁿ N_i (Kulkarni & Fall 2002, Vladilo 2002).

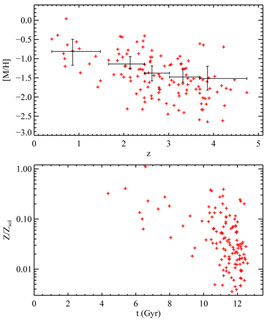Figure 7. Current summary of the metallicity measurements of the damped Ly systems as summarized in Prochaska et al. (2003a), Kulkarni et al. (2004), and Rao et al. (2004). The upper panel plots metallicities against redshift and the binned points indicate the cosmological mean metallicity with 95% confidence level uncertainty. The lower panel plots the metallicity versus look-back time. The overwhelming majority of observations are from t 10 Gyr.

The "age-metallicity" relationship depicted in Figure 7 provides new information about the enrichment history of damped Ly systems. Specifically, the absence of any system with a metallicity [M/H] < -2.6 sets the damped Ly systems apart from the Ly forest. From their analysis of the Ly forest, Simcoe, Sargent & Rauch (2004) find a median abundance, [C,O/H] = -2.8, and find that 30% of their systems have [C,O/H] < -3.5. Schaye et al. (2003) find similar results for [C/H]. While they deduce a higher median abundance for Si, i.e., [Si/H] = -2.0, about 40% of their systems are predicted to have [Si/H] < -2.6. Clearly the bulk of the damped Ly population has a different enrichment history than the Ly forest. To explain the presence of the metallicity floor, Qian & Wasserburg (2003) use a standard chemical evolution model to show that star formation in damped Ly systems results in a rise in metal abundance that is so rapid that the probability for detecting systems with [M/H] < - 2.6 is exceedingly small.

Figure 7 also poses several dilemmas for models of chemical evolution. First, if most of the gas in damped Ly systems in the redshift interval z = [1.6, 4.5] were converted into stars, then most of the stellar mass in current galaxies would be metal poor, contrary to observations (Tremonti et al. 2004). Second, the age-metallicity relation of the thin disk of the Galaxy (Edvardsson et al. 1993) indicates that the thin disk formed at lookback times less than 10 Gyr (i.e., z 1.8) and that chemical enrichment proceeded such that all thin disk stars formed with [M/H] -1.0. But the lower panel in Figure 7 shows that [M/H] < -1.0 in about half of the damped Ly systems with look-back times under 10 Gyr. While this result is subject to the uncertainties of small number statistics and observational bias, the current metallicity trends in low-redshift-damped Ly systems suggest that damped Ly systems may not trace the star-formation history of normal galaxies (Pettini et al. 1999). Third, if the linear increase of < Z > with decreasing redshift deduced at z > 1.6 is extrapolated to z = 0, the current mean metal abundance of galaxies would be equal to -0.69, which appears too low. But since the age-metallicity relationship is essentially unconstrained by the data at z < 1.6, such extrapolations should be treated with caution. Indeed, < Z > is doubling every Gyr at z > 2, and if we assumed < Z > to be a linear function of time rather than redshift, then we would find that < Z > 0 by z 0.5.

3.3. Relative Abundances

In Section 3.2 we described evidence that damped Ly systems are metal poor. We discussed measurements of Zn and Cr that indicate a gas-phase abundance ratio, [Zn/Cr] > 0, implying depletion of Cr by dust. Since metal-poor stars in the Galaxy exhibit different nucleosynthetic abundance ratios than the Sun (Wheeler, Sneden & Truran 1989), the abundance patterns observed in damped Ly systems are probably due to some combination of nucleosynthetic and dust depletion patterns. In this section we briefly describe efforts to unravel these effects. The reader is referred to a series of recent papers for a more thorough discussion of these issues (Pettini 2004, Prochaska & Wolfe 2002, Vladilo 2002b).

3.3.1. DEPLETION

The discussions of metallicity in the previous subsections implicitly assumed that deviations of (X/H)_gas, the gas-phase abundance of element X, from the solar abundance, (X/H), were only due to changes in the intrinsic abundance, (X/H)_int. However, as mentioned previously, (X/H)_gas will also deviate from (X/H) if element X is depleted onto grains. One of the major challenges in damped Ly research is to untangle these two effects.

The traditional method used by most workers in the field is to compare the abundance of refractory element, X, to volatile element, Y, for which (X/Y)_int = (X/Y) in stars with a wide range of absolute abundances. In that case the condition [X/Y] 0 is unlikely to have a nucleosynthetic origin. Rather it likely arises from depletion of the refactory element onto grains. Such a comparison is made in Figure 8a, which is a plot of [Zn/Fe] versus [Zn/H] for a sample of 32 damped Ly systems. The figure reveals an unambiguous correlation between [Zn/Fe] and [Zn/H]: a Kendall -test rules out the null hypothesis of no correlation at more than 99.7% confidence. Because [Zn/Fe] < 0.2 for galactic stars with [Fe/H] > -2.0, the most plausible explanation for this correlation is that in damped Ly systems the depletion of Fe onto grains increases with metal abundance. This argument also suggests that the depletion level decreases with decreasing metal abundance. In that case [Zn/Fe] should approach the intrinsic nucleosynthetic ratio, [Zn/Fe]_int, in the limit [Zn/H] < 0. Determination of [Zn/Fe]_int is important as it indicates the nucleosynthetic history of these elements (Hoffman et al. 1996), and it is required for determining the dust-to-gas ratio, . For example, Wolfe, Prochaska & Gawiser (2003) show that

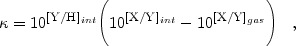(7)

where in this case X = Fe and Y = Zn.

Figure 8. Plot of (a) gas-phase [Zn/Fe] observations against Zn metallicity for all damped Ly systems with high signal-to-noise echelle observations and (b) gas-phase [Si/Fe] observations against Si metallicity for all damped Ly systems with high signal-to-noise echelle observations. Damped Ly systems with upper limits to Zn were suppressed from panel (a). The red arrow in panel (b) corresponds to an upper limit set on [Si/Fe] for one damped Ly system.

Our discussion emphasizes the importance of estimating the intrinsic, nucleosynthetic ratio, [Zn/Fe]_int. On the other hand, the observed Zn abundances are not sufficiently low for the asymptotic approach to [Zn/Fe]_int to be detected. Specifically, because the Zn II transitions are weak, only two damped Ly systems with [Zn/H] < -1.5 have been detected (Lu, Sargent & Barlow 1998; Molaro et al. 2000; Prochaska & Wolfe 2001). By contrast, clouds of such low metallicity can be easily detected in the strong Si II transitions, as shown in Figure 8b, which plots [Si/Fe] versus [Si/H] down to [Si/H] = -2.6. The figure gives convincing evidence that in the limit of vanishing metallicity, [Si/Fe] approaches 0.3 rather than 0. Furthermore, at metallicities [Si/H] > -1 we see evidence for an increase in [Si/Fe] with increasing [Si/H]. This is the same phenomenon seen in the [Zn/Fe] versus [Zn/H] diagram, which we plausibly attributed to dust. The amplitude of the increase is weaker for [Si/Fe] because Si is weakly depleted. On the other hand the increase of [Si/Fe] with [Si/H] is stronger evidence for dust since the nucleosynthetic origin of Si is better understood than that of Zn (Hoffman et al. 1996).

3.3.2. NUCLEOSYNTHETIC ABUNDANCE PATTERNS

3.3.2.1. Enhancements? In Section 3.3.1 we argued that the asymptotic behavior exhibited by the [Si/Fe] ratio in the limit [Si/H] < 0 (Figure 8b) indicated a nucleosynthetic ratio, [Si/Fe]_int 0.3. This asymptotic limit is robust, as it is based on a large number (56) of precision measurements obtained with echelle spectrometers on 8- to 10-m-class telescopes. It also has important implications for the chemical evolution of damped Ly systems if it equals the intrinsic nucleosynthetic ratio. The reason is that disk stars in the Galaxy exhibit a systematic decrease of [/Fe] with increasing [Fe/H], which indicates the increase with time of Fe contributed to the Galaxy ISM by type Ia supernovae relative to type II supernovae (Edvardsson et al. 1993). The presence of such trends in damped Ly systems would support the argument that they are the progenitors of ordinary galaxies. However, the existence of intrinsic enhancements in damped Ly systems is controversial. Using the Vladilo (1998, 2002a) models, Vladilo (2002b) and Ledoux, Bergeron & Petitjean (2002) examined [Si/Fe] ratios corrected for depletion effects and found median values of [Si/Fe]_int consistent with solar. Similarly, several studies of the depletion-free [O/Zn] and [S/Zn] ratios resulted in [/Zn] ratios below those of metal-poor stars (Centurión et al. 2000, Molaro et al. 2000, Nissen et al. 2004).

Is it possible to resolve these conflicts? The lower values of [/Zn] are compatible with the higher value of [/Fe]_int indicated by Figure 8b since [/Fe] = [/Zn] + [Zn/Fe] and Prochaska et al. (2000) and Chen, Kennicutt & Rauch (2004) find [Zn/Fe] 0.15 for thick disk stars with -0.9 < [Fe/H] < -0.6, while Nissen et al. (2004) find [Zn/Fe] 0.1 for stars with [Fe/H] < -1.8. Both results are consistent with [Si/Fe]_int 0.2-0.4. If such enhancements are confirmed in damped Ly systems, one would conclude that the depletion corrections used by Vladilo (2002a) and Ledoux, Bergeron & Petitjean (2002) were too large. The latter are compatible with the dust content suggested by the Pei, Fall & Bechtold (1991) study of reddening in damped Ly systems. But, since the more recent study of Murphy & Liske (2004) argues against such a high dust content, the depletions used to correct the [Si/Fe] ratios may be too large. We also note that [/Fe]_int = 0 would imply significant depletion of Fe at [Si/H] < -1, which is apparently at odds with the insensitivity of [Si/Fe] to increases in [Si/H] shown in Figure 8b. But this behavior may result from two compensating effects: an increase in [Si/Fe] due to Fe depletion and a decrease in [Si/Fe] due to increasing Fe enrichment from type Ia supernovae. Because of these uncertainties, it may be premature to use the [/Fe] ratios in damped Ly systems as discriminants between competing galaxy formation scenarios (e.g., Tolstoy & Venn 2003, Venn et al. 2004).

3.3.2.2. Nitrogen enrichment Pettini, Lipman & Hunstead (1995) first detected nitrogen in damped Ly systems and suggested that the [N / ] versus [ / H] plane could be used as a clock to infer their ages. According to Henry, Edmunds & Köppen (2000) a burst of star formation would coincide with the injection of elements into the surrounding ISM by type II supernovae, followed by the injection of ¹⁴N by AGB stars more than 0.25 Gyr later. In the local Universe, one identifies a plateau of [N / ] values (with value -0.7 dex) at low metallicity presumably consisting of objects with ages greater than 0.25 Gyr. Within this interpretation, metal-poor objects with ages less than 0.25 Gyr would have systematically lower [N / ] values while more evolved damped Ly systems, in which ¹⁴N production has caught up, would have [N / ] - 0.7. Recent studies (Prochaska et al. 2002a, Pettini et al. 2002, Centurión et al. 2003) have shown that the majority of [N / ] values for the damped Ly systems are near the plateau, but there is a population of damped Ly systems with [N / ] -1.5 and very few damped Ly systems with intermediate [N / ] values. The damped Ly systems with [N / ] = -0.7 must be older than 0.25 Gyr. This casts doubt on schemes in which they are transient objects (see Qian & Wasserburg 2003) but rather suggests that they have ages comparable to the age of the Universe at z ~ 3.

The observations also pose a challenge to interpreting the [N / ] value as a strict age diagnostic. If the ages of the damped Ly systems are comparable to 2.5 Gyr, the age of the Universe at z 2.5, then fewer than 10% of the objects would have [N / ] = -1.5, contrary to the current observations. Prochaska et al. (2002a) interpret the paucity of systems with -1.5 < [N / ] < -0.7 as evidence for a bimodal IMF where systems near the plateau at [N / ]=-1.5 are drawn from an IMF truncated from below at M = 7.5 M. In this scenario, damped Ly systems near the plateau at [N / ] = -1.5 need not be younger than 0.25 Gyr, while systems near the plateau at [N / ] = -0.7 are objects older than 0.25 Gyr in which N production is due to the full mass range of intermediate-mass stars drawn from a standard IMF. More recently, Molaro (2003) argued against a bimodal IMF by suggesting that damped Ly systems near the [N / ] = -1.5 plateau are younger than the 0.25 Gyr "catch-up" time. Meynet & Maeder (2002) and Chiappini, Matteucci & Meynet (2003) suggested a mechanism for obtaining a more uniform distribution between the two plateaux. They showed that stellar rotation causes enhanced mixing between the H-burning and He-burning layers, thereby producing greatly enhanced ¹⁴N production in massive stars. Meynet & Maeder (2002) reproduced the [N / ] = -1.5 plateau for stars with M = 8-120 M for rotation speeds vsini = 400 km s^-1. Moreover, rotation may extend the effective lag time between N and production for intermediate mass stars beyond 0.25 Gyr. However, the lack of many damped Ly systems with [N / ] in between -1.5 and -0.7 dex argues against this mechanism and in favor of the bimodal IMF.

3.3.2.3. Metal-strong damped Ly system There exists a small subset of damped Ly systems for which the product of H I column density and metallicity implies very strong "metal-line" transitions. These "metal-strong" damped Ly systems yield abundance measurements for over 20 elements including O, B, Ge, Cu, and Sn. Figure 9 shows the elemental abundance pattern obtained for DLA0812 + 32, the z = 2.626, metal-rich damped Ly system discussed in Section 3.1 (Prochaska, Howk & Wolfe 2003). This is the first damped Ly system for which absolute abundances for B and Ge have been determined, and it is one of the few objects for which an accurate measurement of [O/H] is possible. With the detection of over 20 elements, the metal-strong damped Ly systems permit a global inspection of its enrichment history. The dotted line in Figure 9 is the solar abundance pattern scaled to oxygen. The good match to the data shows that this system exhibits an enrichment pattern resembling that of the Sun. Furthermore, specific abundance ratios constrain various nucleosynthetic processes in the young Universe. For example, the abundance of the odd-Z elements P, Ga, and Mn compared to Si, Ge, and Fe indicates an enhanced "odd-even effect" and impact theories of explosive nucleosynthesis. Similarly, measurements of the B/O ratio help develop theories of light element nucleosynthesis while constraints on Sn, Kr, and other heavy elements will test scenarios of the r- and s-process.

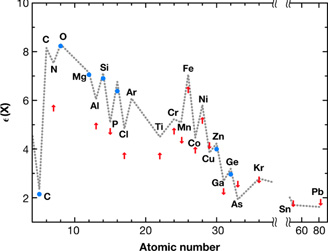Figure 9. Abundance pattern for the metal-strong damped Ly system at z = 2.626 toward Q0812 + 32. Because of the high metal abundance, [O/H] = -0.44, a dust correction is necessary, and in this case a conservative "warm halo" correction (Savage & Sembach 1996) was applied. The dotted line traces the Solar abundance pattern scaled to match the oxygen abundance of the damped Ly system. The red arrows are lower and upper limits on e(X) and the blue dots correspond to measured values of e(X).

³ Here and in what follows the relative abundance of elements X and Y is defined with respect to the solar abundance on a logarithmic scale; i.e. [X/Y] = log₁₀(X/Y) - log₁₀(X/Y). Back.

⁴ Here and in what follows we designate a damped Ly system toward a QSO with coordinates hhmm±deg as DLAhhmm±deg. Back.