


In the previous section we have learn that galaxy formation and
evolution are definitively related to cosmological conditions.
Cosmology provides the theoretical framework for the
initial and boundary conditions of the cosmic structure formation
models. At the same time, the confrontation of model predictions
with astronomical observations became the most powerful testbed
for cosmology. As a result of this fruitful convergence between
cosmology and astronomy, there emerged the current paradigmatic scenario
of cosmic structure formation and evolution of the Universe
called  Cold Dark
Matter (
Cold Dark
Matter ( CDM). The
CDM). The
 CDM scenario
integrates nicely: (1) cosmological theories (Big Bang and Inflation),
(2) physical models (standard and extensions of the particle physics
models), (3) astrophysical models (gravitational cosmic structure
growth, hierarchical clustering, gastrophysics), and (4) phenomenology
(CMBR anisotropies, non-baryonic DM, repulsive dark energy, flat
geometry, galaxy properties).
CDM scenario
integrates nicely: (1) cosmological theories (Big Bang and Inflation),
(2) physical models (standard and extensions of the particle physics
models), (3) astrophysical models (gravitational cosmic structure
growth, hierarchical clustering, gastrophysics), and (4) phenomenology
(CMBR anisotropies, non-baryonic DM, repulsive dark energy, flat
geometry, galaxy properties).
Nowadays, cosmology passed from being the Cinderella of astronomy
to be one of the highest precision sciences. Let us consider only the
Inflation/Big Bang cosmological models with the F-R-W
metric and adiabatic perturbations. The number of parameters that
characterize these models is high, around 15 to be more precise.
No single cosmological probe constrain all of these parameters. By using
multiple data sets and probes it is possible to constrain with precision
several of these parameters, many of which correlate among them
(degeneracy). The main cosmological probes used for
precision cosmology are the CMBR anisotropies, the type-Ia SNe and long
Gamma-Ray Bursts,
the Ly power spectrum,
the large-scale power spectrum from
galaxy surveys, the cluster of galaxies dynamics and abundances, the
peculiar velocity surveys, the weak and strong lensing,
the baryonic acoustic oscillation in the large-scale galaxy distribution.
There is a model that is systematically consistent with most of these probes
and one of the goals in the last years has been to improve the error
bars of the parameters for this 'concordance' model. The geometry in the
concordance model is flat with an energy composition dominated in ~ 2/3 by
the cosmological constant
power spectrum,
the large-scale power spectrum from
galaxy surveys, the cluster of galaxies dynamics and abundances, the
peculiar velocity surveys, the weak and strong lensing,
the baryonic acoustic oscillation in the large-scale galaxy distribution.
There is a model that is systematically consistent with most of these probes
and one of the goals in the last years has been to improve the error
bars of the parameters for this 'concordance' model. The geometry in the
concordance model is flat with an energy composition dominated in ~ 2/3 by
the cosmological constant
 (generically
called Dark Energy),
responsible for the current accelerated expansion of the Universe. The other
~ 1/3 is matter, but ~ 85% of this 1/3 is in form of
non-baryonic DM. Table 2 presents the central
values of different parameters of the
(generically
called Dark Energy),
responsible for the current accelerated expansion of the Universe. The other
~ 1/3 is matter, but ~ 85% of this 1/3 is in form of
non-baryonic DM. Table 2 presents the central
values of different parameters of the
 CDM cosmology from
combined model fittings
to the recent 3-year WMAP CMBR and several other cosmological probes
[109]
(see the WMAP website).
CDM cosmology from
combined model fittings
to the recent 3-year WMAP CMBR and several other cosmological probes
[109]
(see the WMAP website).
| Parameter | Constraint |
| Total density |  = 1
= 1 |
| Dark Energy density |   = 0.74 = 0.74 |
| Dark Matter density |  DM = 0.216 DM = 0.216 |
| Baryon Matter dens. |  B = 0.044 B = 0.044 |
| Hubble constant | h = 0.71 |
| Age | 13.8 Gyr |
| Power spectrum norm. |  8 = 0.75 8 = 0.75 |
| Power spectrum index | ns(0.002) = 0.94 |
In the following, I will describe some of the ingredients of the
 CDM scenario,
emphasizing that most of these ingredients are well established aspects
that any alternative scenario to
CDM scenario,
emphasizing that most of these ingredients are well established aspects
that any alternative scenario to
 CDM should be able
to explain.
CDM should be able
to explain.
The Big Bang 4 is now a mature theory, based on well established observational pieces of evidence. However, the Big Bang theory has limitations. One of them is namely the origin of fluctuations that should give rise to the highly inhomogeneous structure observed today in the Universe, at scales of less than ~ 200 Mpc. The smaller the scales, the more clustered is the matter. For example, the densities inside the central regions of galaxies, within the galaxies, cluster of galaxies, and superclusters are about 1011, 106, 103 and few times the average density of the Universe, respectively.
The General Relativity equations that describe the Universe dynamics
in the Big Bang theory are for an homogeneous and isotropic fluid
(Cosmological Principle); inhomogeneities are not taken into
account in this theory "by definition". Instead, the concept
of fluctuations is inherent to the Inflationary theory introduced
in the early 80's by A. Guth and A. Linde namely to overcome the
Big Bang limitations. According to this theory, at the energies
of Grand Unification
( 1014 GeV or T
1014 GeV or T
 1027 K!),
the matter was in the state known in quantum field theory as vacuum.
Vacuum is characterized by quantum fluctuations -temporary changes
in the amount of energy in a point in space, arising from Heisenberg
uncertainty principle. For a small time interval
1027 K!),
the matter was in the state known in quantum field theory as vacuum.
Vacuum is characterized by quantum fluctuations -temporary changes
in the amount of energy in a point in space, arising from Heisenberg
uncertainty principle. For a small time interval
 t, a virtual
particle-antiparticle pair of energy
t, a virtual
particle-antiparticle pair of energy
 E is created
(in the GU theory, the field particles are supposed to be the X- and
Y-bossons), but then the pair disappears so that there is no violation
of energy conservation. Time and energy are related by
E is created
(in the GU theory, the field particles are supposed to be the X- and
Y-bossons), but then the pair disappears so that there is no violation
of energy conservation. Time and energy are related by
 E
E
 t
t
 h /
2
h /
2 . The vacuum quantum
fluctuations are proposed to be the seeds of present-day
structures in the Universe.
. The vacuum quantum
fluctuations are proposed to be the seeds of present-day
structures in the Universe.
How is that quantum fluctuations become density inhomogeneities?
During the inflationary period, the expansion is described approximately
by the de Sitter cosmology, a
 eHt,
H
eHt,
H 
 / a is the
Hubble parameter and it is constant in this cosmology. Therefore, the
proper length of any fluctuation grows as
/ a is the
Hubble parameter and it is constant in this cosmology. Therefore, the
proper length of any fluctuation grows as
 p
p
 eHt. On the other hand, the proper radius of the
horizon for de Sitter metric is equal to c / H = const,
so that initially causally connected (quantum) fluctuations become
suddenly supra-horizon (classical) perturbations to the spacetime
metric. After inflation, the Hubble radius grows proportional to
ct, and at some time a given curvature
perturbation cross again the horizon (becomes causally connected,
eHt. On the other hand, the proper radius of the
horizon for de Sitter metric is equal to c / H = const,
so that initially causally connected (quantum) fluctuations become
suddenly supra-horizon (classical) perturbations to the spacetime
metric. After inflation, the Hubble radius grows proportional to
ct, and at some time a given curvature
perturbation cross again the horizon (becomes causally connected,
 p <
LH). It becomes now a true density perturbation. The
interesting aspect of the perturbation 'trip' outside the horizon is
that its amplitude remains roughly constant, so that if the amplitude of
the fluctuations at the time of exiting the horizon during inflation is
constant (scale invariant), then their amplitude at the time of entering
the horizon should be also scale
invariant. In fact, the computation of classical perturbations generated
by a quantum field during inflation demonstrates that the amplitude of
the scalar fluctuations at the time of crossing the horizon is nearly
constant,
p <
LH). It becomes now a true density perturbation. The
interesting aspect of the perturbation 'trip' outside the horizon is
that its amplitude remains roughly constant, so that if the amplitude of
the fluctuations at the time of exiting the horizon during inflation is
constant (scale invariant), then their amplitude at the time of entering
the horizon should be also scale
invariant. In fact, the computation of classical perturbations generated
by a quantum field during inflation demonstrates that the amplitude of
the scalar fluctuations at the time of crossing the horizon is nearly
constant,

 H
H
 const. This can be
understood on dimensional grounds: due to the Heisenberg principle
const. This can be
understood on dimensional grounds: due to the Heisenberg principle

 /
/
 t
t
 const,
where
const,
where  t
t
 H-1. Therefore,
H-1. Therefore,

 H
H
 H, but H
is roughly constant during inflation, so that
H, but H
is roughly constant during inflation, so that

 H
H
 const.
const.
3.2. Gravitational evolution of fluctuations
The  CDM scenario
assumes the gravitational instability paradigm:
the cosmic structures in the Universe were formed as a consequence of
the growth of primordial tiny fluctuations (for example seeded in the
inflationary epochs) by gravitational instability in an expanding frame.
The fluctuation or perturbation is characterized by its density contrast,
CDM scenario
assumes the gravitational instability paradigm:
the cosmic structures in the Universe were formed as a consequence of
the growth of primordial tiny fluctuations (for example seeded in the
inflationary epochs) by gravitational instability in an expanding frame.
The fluctuation or perturbation is characterized by its density contrast,
 |
(1) |
where  is the average density of the Universe and
is the average density of the Universe and
 is the
perturbation density. At early epochs,
is the
perturbation density. At early epochs,
 << 1
for perturbation of all scales, otherwise the homogeneity condition
in the Big Bang theory is not anymore obeyed. When
<< 1
for perturbation of all scales, otherwise the homogeneity condition
in the Big Bang theory is not anymore obeyed. When
 << 1, the
perturbation is in the linear regime and its physical size grows
with the expansion proportional to a(t). The perturbation
analysis in the linear approximation shows whether a given perturbation
is stable (
<< 1, the
perturbation is in the linear regime and its physical size grows
with the expansion proportional to a(t). The perturbation
analysis in the linear approximation shows whether a given perturbation
is stable ( ~ const or
even
~ const or
even  0) or unstable
(
0) or unstable
( grows).
In the latter case, when
grows).
In the latter case, when 
 1, the linear
approximation
is not anymore valid, and the perturbation "separates" from the expansion,
collapses, and becomes a self-gravitating structure. The gravitational
evolution in the non-linear regime is complex for realistic
cases and is studied with numerical N-body simulations. Next,
a pedagogical review of the linear evolution of perturbations is presented.
More detailed explanations on this subject can be found in the books
[72,
94,
90,
30,
77,
92].
1, the linear
approximation
is not anymore valid, and the perturbation "separates" from the expansion,
collapses, and becomes a self-gravitating structure. The gravitational
evolution in the non-linear regime is complex for realistic
cases and is studied with numerical N-body simulations. Next,
a pedagogical review of the linear evolution of perturbations is presented.
More detailed explanations on this subject can be found in the books
[72,
94,
90,
30,
77,
92].
Relevant times and scales.
The important times in the problem of linear gravitational evolution of
perturbations are: (a) the epoch when inflation
finished (tinf
 10-34 s,
at this time the primordial fluctuation
field is established); (b) the epoch of matter-radiation equality
teq (corresponding to aeq
10-34 s,
at this time the primordial fluctuation
field is established); (b) the epoch of matter-radiation equality
teq (corresponding to aeq
 1/3.9 ×
104(
1/3.9 ×
104( 0 h2), before
teq the dynamics of the universe is dominated by
radiation density,
after teq dominates matter density); (c) the epoch of
recombination trec,
when radiation decouples from baryonic matter (corresponding
to arec=1/1080, or trec
0 h2), before
teq the dynamics of the universe is dominated by
radiation density,
after teq dominates matter density); (c) the epoch of
recombination trec,
when radiation decouples from baryonic matter (corresponding
to arec=1/1080, or trec
 3.8 ×
105yr for the concordance cosmology).
3.8 ×
105yr for the concordance cosmology).
Scales: first of all, we need to characterize
the size of the perturbation. In the linear regime, its physical size
expands with the Universe:
 p =
a(t)
p =
a(t)
 0, where
0, where
 0 is the
comoving size, by convention fixed (extrapolated) to the present epoch,
a(t0) = 1. In a given (early) epoch, the size
of the perturbation can be larger than the so-called Hubble
radius, the typical radius over which
physical processes operate coherently (there is causal connection):
LH
0 is the
comoving size, by convention fixed (extrapolated) to the present epoch,
a(t0) = 1. In a given (early) epoch, the size
of the perturbation can be larger than the so-called Hubble
radius, the typical radius over which
physical processes operate coherently (there is causal connection):
LH
 (a /
(a /
 )-1 =
H-1 = n-1
ct. For the radiation or matter
dominated cases, a(t)
)-1 =
H-1 = n-1
ct. For the radiation or matter
dominated cases, a(t)
 tn,
with n = 1/2 and n = 2/3, respectively,
that is n < 1. Therefore, LH grows faster
than
tn,
with n = 1/2 and n = 2/3, respectively,
that is n < 1. Therefore, LH grows faster
than  p and
at a given "crossing" time tcross,
p and
at a given "crossing" time tcross,
 p <
LH. Thus, the
perturbation is supra-horizon sized at epochs t <
tcross and sub-horizon
sized at t > tcross. Notice that if n
> 1, then at some time the
perturbation "exits" the Hubble radius. This is what happens in the
inflationary epoch, when a(t)
p <
LH. Thus, the
perturbation is supra-horizon sized at epochs t <
tcross and sub-horizon
sized at t > tcross. Notice that if n
> 1, then at some time the
perturbation "exits" the Hubble radius. This is what happens in the
inflationary epoch, when a(t)
 et:
causally-connected fluctuations of any size are are suddenly "taken out"
outside the Hubble radius becoming causally disconnected.
et:
causally-connected fluctuations of any size are are suddenly "taken out"
outside the Hubble radius becoming causally disconnected.
For convenience, in some cases it is better to use masses instead of sizes.
Since in the linear regime
 << 1
(
<< 1
(

 ),
then M
),
then M 
 M(a)
M(a)
 3, where
3, where
 is the size of a
given region of the Universe with average matter density
is the size of a
given region of the Universe with average matter density
 M. The
mass of the perturbation, Mp, is invariant.
M. The
mass of the perturbation, Mp, is invariant.
Supra-horizon sized perturbations.
In this case, causal, microphysical processes are not possible, so that it does not matter what perturbations are made of (baryons, radiation, dark matter, etc.); they are in general just perturbations to the metric. To study the gravitational growth of metric perturbations, a General Relativistic analysis is necessary. A major issue in carrying out this program is that the metric perturbation is not a gauge invariant quantity. See e.g., [72] for an outline of how E. Lifshitz resolved brilliantly this difficult problem in 1946. The result is quite simple and it shows that the amplitude of metric perturbations outside the horizon grows kinematically at different rates, depending on the dominant component in the expansion dynamics. For the critical cosmological model (at early epochs all models approach this case), the growing modes of metric perturbations according to what dominates the background are:
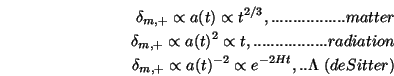 |
(2) (3) |
Sub-horizon sized perturbations.
Once perturbations are causally connected, microphysical processes are
switched on (pressure, viscosity, radiative transport, etc.)
and the gravitational evolution of the perturbation depends
on what it is made of. Now, we deal with true density perturbations.
For them applies the classical perturbation analysis for a fluid,
originally introduced by J. Jeans in 1902, in the context of the problem
of star formation in the ISM.
But unlike in the ISM, in the cosmological context the fluid
is expanding. What can prevent the perturbation amplitude from growing
gravitationally? The answer is pressure support. If the fluid pressure
gradient can re-adjust itself in a timescale tpress
smaller than the gravitational collapse timescale,
tgrav, then pressure prevents the gravitational
growth of  . Thus, the
condition for gravitational instability is:
. Thus, the
condition for gravitational instability is:
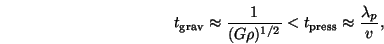 |
(4) |
where  is the
density of the component that is most
gravitationally dominant in the Universe, and v is the sound speed
(collisional fluid) or velocity dispersion (collisionless fluid) of the
perturbed component. In other words, if the perturbation scale is larger
than a critical scale
is the
density of the component that is most
gravitationally dominant in the Universe, and v is the sound speed
(collisional fluid) or velocity dispersion (collisionless fluid) of the
perturbed component. In other words, if the perturbation scale is larger
than a critical scale
 J ~
v(G
J ~
v(G
 )-1/2,
then pressure loses, gravity wins.
)-1/2,
then pressure loses, gravity wins.
The perturbation analysis applied to the
hydrodynamical equations of a fluid at rest shows that
 grows exponentially with time for perturbations obeying the
Jeans instability criterion
grows exponentially with time for perturbations obeying the
Jeans instability criterion
 p >
p >
 J, where the
exact value of
J, where the
exact value of
 J is
v(
J is
v( / G
/ G
 )1/2.
If
)1/2.
If  p
<
p
<  J,
then the perturbations are described by stable gravito-acustic
oscillations. The situation is conceptually similar for
perturbations in an expanding cosmological fluid, but the growth of
J,
then the perturbations are described by stable gravito-acustic
oscillations. The situation is conceptually similar for
perturbations in an expanding cosmological fluid, but the growth of
 in the unstable
regime is algebraical instead of exponential. Thus, the cosmic
structure formation process is relatively slow. Indeed, the typical
epochs of galaxy and cluster of galaxies formation are at redshifts
z ~ 1 - 5 (ages of ~ 1.2 - 6 Gyrs) and z < 1 (ages larger
than 6 Gyrs), respectively.
in the unstable
regime is algebraical instead of exponential. Thus, the cosmic
structure formation process is relatively slow. Indeed, the typical
epochs of galaxy and cluster of galaxies formation are at redshifts
z ~ 1 - 5 (ages of ~ 1.2 - 6 Gyrs) and z < 1 (ages larger
than 6 Gyrs), respectively.
Baryonic matter. The Jeans instability analysis for a
relativistic (plasma) fluid of baryons ideally
coupled to radiation and expanding at the rate H =
 / a shows that
there is an instability critical scale
/ a shows that
there is an instability critical scale
 J =
v(3
J =
v(3 / 8G
/ 8G
 )1/2,
where the sound speed for adiabatic perturbations is v = p /
)1/2,
where the sound speed for adiabatic perturbations is v = p /
 = c
/ (3)1/2; the latter
equality is due to pressure radiation. At the epoch when
radiation dominates,
= c
/ (3)1/2; the latter
equality is due to pressure radiation. At the epoch when
radiation dominates,
 =
=
 r
r
 a-4
and then
a-4
and then  J
J
 a2
a2
 ct. It is not
surprising that at this
epoch
ct. It is not
surprising that at this
epoch  J
approximates the Hubble scale LH
J
approximates the Hubble scale LH
 ct
(it is in fact ~ 3 times larger). Thus, perturbations that might
collapse gravitationally are in fact outside the horizon, and those
that already entered the horizon, have scales smaller than
ct
(it is in fact ~ 3 times larger). Thus, perturbations that might
collapse gravitationally are in fact outside the horizon, and those
that already entered the horizon, have scales smaller than
 J:
they are stable gravito-acoustic oscillations. When matter
dominates,
J:
they are stable gravito-acoustic oscillations. When matter
dominates,  =
=  M
M
 a-3, and a
a-3, and a
 t2/3.
Therefore,
t2/3.
Therefore,  J
J
 a
a
 t2/3
t2/3
 LH, but still
radiation is coupled to baryons, so that radiation pressure is dominant
and
LH, but still
radiation is coupled to baryons, so that radiation pressure is dominant
and  J
remains large. However, when radiation decouples
from baryons at trec, the pressure support drops
dramatically by a factor of Pr / Pb
J
remains large. However, when radiation decouples
from baryons at trec, the pressure support drops
dramatically by a factor of Pr / Pb
 nr
T / nb T
nr
T / nb T
 108! Now,
the Jeans analysis for a gas mix of H and He at temperature
Trec
108! Now,
the Jeans analysis for a gas mix of H and He at temperature
Trec  4000 K shows that baryonic clouds with masses
4000 K shows that baryonic clouds with masses
 106
M
106
M can collapse
gravitationally, i.e. all masses of
cosmological interest. But this is literally too "ideal" to be true.
can collapse
gravitationally, i.e. all masses of
cosmological interest. But this is literally too "ideal" to be true.
The problem is that as the Universe expands, radiation cools
(Tr = T0 a-1)
and the photon-baryon fluid becomes less and less perfect: the mean free
path for scattering of photons by electrons (which at the same time
are coupled electrostatically to the protons) increases. Therefore,
photons can
diffuse out of the bigger and bigger density perturbations as the photon
mean free path increases. If perturbations are in the gravito-acoustic
oscillatory regime, then the oscillations are damped out and the
perturbations disappear. The "ironing out" of perturbations continues until
the epoch of recombination. In a pioneering work, J. Silk
[104]
carried out a perturbation analysis of a relativistic cosmological fluid
taking into account radiative transfer in the diffusion approximation. He
showed that all photon-baryon perturbations of masses smaller than
Ms are "ironed out" until trec by
the (Silk) damping process. The first crisis in galaxy formation theory
emerged: calculations showed that
Ms is of the order of 1013 - 1014
M h-1! If somebody
(god, inflation, ...) seeded primordial fluctuations in the Universe,
by Silk damping all galaxy-sized perturbation are "ironed out".
5
h-1! If somebody
(god, inflation, ...) seeded primordial fluctuations in the Universe,
by Silk damping all galaxy-sized perturbation are "ironed out".
5
Non-baryonic matter. The gravito-acoustic oscillations and their
damping by photon diffusion
refer to baryons. What happens for a fluid of non-baryonic DM?
After all, astronomers, since Zwicky in the 1930s, find routinely pieces
of evidence for the presence of large amounts of DM in the Universe.
As DM is assumed to be collisionless and not interacting
electromagnetically, then the radiative or thermal pressure supports are
not important for linear DM perturbations. However, DM perturbations can be
damped out by free streaming if the particles are relativistic: the
geodesic motion of the particles at the speed of light will iron out any
perturbation smaller than a scale close to the particle horizon radius,
because the particles can freely propagate from an overdense region to an
underdense region. Once the particles cool and become non relativistic,
free streaming is not anymore important. A particle of mass
mX and
temperature TX becomes non relativistic when
kB TX ~ mX
c2. Since TX
 a-1, and a
a-1, and a
 t1/2 when radiation dominates,
one then finds that the epoch when a thermal-relic particle becomes non
relativistic is tnr
t1/2 when radiation dominates,
one then finds that the epoch when a thermal-relic particle becomes non
relativistic is tnr
 mX-2. The more massive the DM particle, the
earlier it becomes non relativistic, and the smaller are therefore the
perturbations damped out by free streaming (those smaller than ~
ct; see Fig. 4). According to the epoch
when a given thermal DM particle species
becomes non relativistic, DM is called Cold Dark Matter (CDM, very early),
Warm Dark Matter (WDM, early) and Hot Dark Matter (HDM, late)
6.
mX-2. The more massive the DM particle, the
earlier it becomes non relativistic, and the smaller are therefore the
perturbations damped out by free streaming (those smaller than ~
ct; see Fig. 4). According to the epoch
when a given thermal DM particle species
becomes non relativistic, DM is called Cold Dark Matter (CDM, very early),
Warm Dark Matter (WDM, early) and Hot Dark Matter (HDM, late)
6.
The only non-baryonic particles confirmed experimentally are (light) neutrinos (HDM). For neutrinos of masses ~ 1 - 10eV, free streaming attains to iron out perturbations of scales as large as massive clusters and superclusters of galaxies (see Fig. 4). Thus, HDM suffers the same problem of baryonic matter concerning galaxy formation 7. At the other extreme is CDM, in which case survive free streaming practically all scales of cosmological interest. This makes CDM appealing to galaxy formation theory. In the minimal CDM model, it is assumed that perturbations of all scales survive, and that CDM particles are collisionless (they do not self-interact). Thus, if CDM dominates, then the first step in galaxy formation study is reduced to the calculation of the linear and non-linear gravitational evolution of collisionless CDM perturbations. Galaxies are expected to form in the centers of collapsed CDM structures, called halos, from the baryonic gas, first trapped in the gravitational potential of these halos, and second, cooled by radiative (and turbulence) processes (see Section 5).
The CDM perturbations are free of any physical damping processes and
in principle their amplitudes may grow by gravitational instability.
However, when radiation dominates, the perturbation growth is
stagnated by expansion. The gravitational instability timescale for
sub-horizon linear CDM perturbations is tgrav ~
(G  DM)-2,
while the expansion (Hubble) timescale is given by
texp ~ (G
DM)-2,
while the expansion (Hubble) timescale is given by
texp ~ (G
 )-2. When radiation dominates,
)-2. When radiation dominates,


 r
and
r
and  r
>>
r
>>
 M.
Therefore texp << tgrav, that
is, expansion is faster than the gravitational shrinking.
M.
Therefore texp << tgrav, that
is, expansion is faster than the gravitational shrinking.
Fig. 5 resumes the evolution of primordial
perturbations. Instead of spatial scales, in Fig. 5
are shown masses, which are invariant for the perturbations. We
highlight the following conclusions
from this plot: (1) Photon-baryon perturbations of masses <
Ms are washed
out ( B
B
 0) as long as baryon
matter is coupled to radiation.
(2) The amplitude of CDM perturbations that enter the horizon before
teq is "freezed-out"
(
0) as long as baryon
matter is coupled to radiation.
(2) The amplitude of CDM perturbations that enter the horizon before
teq is "freezed-out"
( DM
DM
 const)
as long as radiation dominates; these are perturbations of masses
smaller than MH,eq
const)
as long as radiation dominates; these are perturbations of masses
smaller than MH,eq
 1013(
1013( M h2)-2
M
M h2)-2
M , namely
galaxy scales. (3) The
baryons are trapped gravitationally by CDM perturbations, and within a
factor of two in z, baryon perturbations attain amplitudes half
that of
, namely
galaxy scales. (3) The
baryons are trapped gravitationally by CDM perturbations, and within a
factor of two in z, baryon perturbations attain amplitudes half
that of  DM.
For WDM or HDM perturbations, the free-streaming damping
introduces a mass scale Mfs
DM.
For WDM or HDM perturbations, the free-streaming damping
introduces a mass scale Mfs
 MH,n.r. in Fig. 5, below
which
MH,n.r. in Fig. 5, below
which 
 0;
Mfs increases as the DM mass particle decreases
(Fig. 4).
0;
Mfs increases as the DM mass particle decreases
(Fig. 4).
The processed power spectrum of perturbations. The exact solution to the problem of linear evolution of cosmological perturbations is much more complex than the conceptual aspects described above. Starting from a primordial fluctuation field, the perturbation analysis should be applied to a cosmological mix of baryons, radiation, neutrinos, and other non-baryonic dark matter components (e.g., CDM), at sub- and supra-horizon scales (the fluid assumption is relaxed). Then, coupled relativistic hydrodynamic and Boltzmann equations in a general relativity context have to be solved taking into account radiative and dissipative processes. The outcome of these complex calculations is the full description of the processed fluctuation field at the recombination epoch (when fluctuations at almost all scales are still in the linear regime). The goal is double and of crucial relevance in cosmology and astrophysics: 1) to predict the physical and statistical properties of CMBR anisotropies, which can be then compared with observations, and 2) to provide the initial conditions for calculating the non-linear regime of cosmic structure formation and evolution. Fortunately, there are now several public friendly-to-use codes that numerically solve the cosmological linear perturbation equations (e.g., CMBFast and CAMB 8).
The description of the density fluctuation field is statistical. As any
random field, it is convenient to study perturbations in the Fourier space.
The Fourier expansion of
 (x) is:
(x) is:
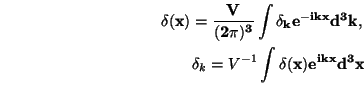 |
(5) (6) |
The Fourier modes
 k evolve
independently while the perturbations are in
the linear regime, so that the perturbation analysis can be applied to this
quantity. For a Gaussian random field, any statistical
quantity of interest can be specified in terms of the power spectrum
P(k)
k evolve
independently while the perturbations are in
the linear regime, so that the perturbation analysis can be applied to this
quantity. For a Gaussian random field, any statistical
quantity of interest can be specified in terms of the power spectrum
P(k)  |
| k|2,
which measures the amplitude of the fluctuations at
a given scale k
9. Thus, from the linear
perturbation analysis we may follow the evolution of
P(k). A more intuitive quantity than P(k) is
the mass variance
k|2,
which measures the amplitude of the fluctuations at
a given scale k
9. Thus, from the linear
perturbation analysis we may follow the evolution of
P(k). A more intuitive quantity than P(k) is
the mass variance
 M2
M2
 <(
<( M /
M)r2> of the fluctuation field.
The physical meaning of
M /
M)r2> of the fluctuation field.
The physical meaning of
 M is that of
an rms density contrast on a given
sphere of radius R associated to the mass M =
M is that of
an rms density contrast on a given
sphere of radius R associated to the mass M =
 VW(R), where W(R)
is a window (smoothing) function. The mass variance is related to
P(k). By
assuming a power law power spectrum, P(k)
VW(R), where W(R)
is a window (smoothing) function. The mass variance is related to
P(k). By
assuming a power law power spectrum, P(k)
 kn,
it is easy to show that
kn,
it is easy to show that
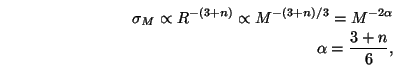 |
(7) |
for 4 < n < -3 using a Gaussian window function. The
question is: How the scaling law of perturbations,
 M, evolves
starting from an initial
(
M, evolves
starting from an initial
( M)i?
M)i?
In the early 1970s, Harrison and Zel'dovich independently asked themselves
about the functionality of
 M (or the
density contrast) at the time adiabatic
perturbations cross the horizon, that is, if
(
M (or the
density contrast) at the time adiabatic
perturbations cross the horizon, that is, if
( M)H
M)H
 M
M H, then what is the value of
H, then what is the value of
 H? These
authors concluded that -0.1
H? These
authors concluded that -0.1 
 H
H
 0.2,
i.e.
0.2,
i.e.  H
H
 0
(nH
0
(nH  -3). If
-3). If  H
>> 0 (nH >> -3), then
H
>> 0 (nH >> -3), then
 M
M

 for
M
for
M  0; this
means that for a given small mass scale M,
the mass density of the perturbation at the time of becoming causally
connected can correspond to the one of a (primordial) black
hole. Hawking evaporation of black holes put a constraint on
MBH,prim
0; this
means that for a given small mass scale M,
the mass density of the perturbation at the time of becoming causally
connected can correspond to the one of a (primordial) black
hole. Hawking evaporation of black holes put a constraint on
MBH,prim
 1015
g, which corresponds
to
1015
g, which corresponds
to  H
H
 0.2, otherwise the
0.2, otherwise the
 -ray
background radiation would be more intense than that observed. If
-ray
background radiation would be more intense than that observed. If
 H
<< 0 (nH << -3), then larger scales
would be denser than the small ones, contrary to what is observed. The
scale-invariant Harrison-Zel'dovich power spectrum,
PH(k)
H
<< 0 (nH << -3), then larger scales
would be denser than the small ones, contrary to what is observed. The
scale-invariant Harrison-Zel'dovich power spectrum,
PH(k)
 k-3, is for perturbations at the time of entering the
horizon. How should the primordial power spectrum
Pi(k) = Akin or
(
k-3, is for perturbations at the time of entering the
horizon. How should the primordial power spectrum
Pi(k) = Akin or
( M)i
= BM-
M)i
= BM- i (defined at some fixed initial time)
be to produce such scale invariance? Since ti until
the horizon crossing time
tcross(M) for a given perturbation of mass
M,
i (defined at some fixed initial time)
be to produce such scale invariance? Since ti until
the horizon crossing time
tcross(M) for a given perturbation of mass
M,
 M(t)
evolves as a(t)2
(supra-horizon regime in the radiation era).
At tcross, the horizon mass MH is
equal by definition to M. We have
seen that MH
M(t)
evolves as a(t)2
(supra-horizon regime in the radiation era).
At tcross, the horizon mass MH is
equal by definition to M. We have
seen that MH
 a3
(radiation dominion), so that across
a3
(radiation dominion), so that across
 MH1/3 = M1/3. Therefore,
MH1/3 = M1/3. Therefore,
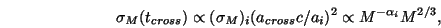 |
(8) |
i.e.  H = 2/3
-
H = 2/3
-  i or
nH = ni - 4. A similar result is
obtained if the perturbation enters the horizon during the matter
dominion era. From this analysis
one concludes that for the perturbations to be scale invariant at horizon
crossing (
i or
nH = ni - 4. A similar result is
obtained if the perturbation enters the horizon during the matter
dominion era. From this analysis
one concludes that for the perturbations to be scale invariant at horizon
crossing ( H =
0 or nH = -3), the primordial (initial) power spectrum
should be Pi(k) = Ak1 or
(
H =
0 or nH = -3), the primordial (initial) power spectrum
should be Pi(k) = Ak1 or
( M)i
M)i
 M-2/3
M-2/3 
 0-2
(i.e. ni = 1 and
0-2
(i.e. ni = 1 and
 = 2/3; A is a
normalization constant). Does inflation predict such power spectrum?
We have seen that, according to the quantum field theory and assuming that
H = const during inflation, the fluctuation amplitude is scale
invariant at the time to exit the horizon,
= 2/3; A is a
normalization constant). Does inflation predict such power spectrum?
We have seen that, according to the quantum field theory and assuming that
H = const during inflation, the fluctuation amplitude is scale
invariant at the time to exit the horizon,
 H ~ const. On
the other hand, we have seen
that supra-horizon curvature perturbations during a de Sitter period
evolve as
H ~ const. On
the other hand, we have seen
that supra-horizon curvature perturbations during a de Sitter period
evolve as 
 a-2
(eq. 4). Therefore, at the end of inflation we have that
a-2
(eq. 4). Therefore, at the end of inflation we have that
 inf =
inf =
 H(
H( 0)(ainf /
aH)-2.
The proper size of the fluctuation when crossing the horizon is
0)(ainf /
aH)-2.
The proper size of the fluctuation when crossing the horizon is
 p =
aH
p =
aH
 0
0
 H-1; therefore, aH
H-1; therefore, aH
 1 /
(
1 /
( 0 H).
Replacing now this expression in the equation for
0 H).
Replacing now this expression in the equation for
 inf we get that:
inf we get that:
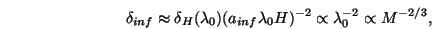 |
(9) |
if  H ~
const. Thus, inflation predicts
H ~
const. Thus, inflation predicts
 i
nearly equal to 2/3 (ni
i
nearly equal to 2/3 (ni
 1)!
Recent results from the analysis of CMBR anisotropies by the WMAP
satellite
[109]
seem to show that ni is slightly smaller than 1 or
that ni changes with the scale (running power-spectrum
index). This is in more agreement with several inflationary models,
where H actually
slightly vary with time introducing some scale dependence in
1)!
Recent results from the analysis of CMBR anisotropies by the WMAP
satellite
[109]
seem to show that ni is slightly smaller than 1 or
that ni changes with the scale (running power-spectrum
index). This is in more agreement with several inflationary models,
where H actually
slightly vary with time introducing some scale dependence in
 H.
H.
The perturbation analysis, whose bases were presented in
Section 3.2 and
resumed in Fig. 5, show us that
 M grows
(kinematically) while perturbations are in the supra-horizon
regime. Once perturbations enter the horizon (first the smaller ones),
if they are made of CDM, then the gravitational growth is "freezed out"
whilst radiation dominates (stangexpantion). As shown
schematically in Fig. 6, this "flattens" the
variance
M grows
(kinematically) while perturbations are in the supra-horizon
regime. Once perturbations enter the horizon (first the smaller ones),
if they are made of CDM, then the gravitational growth is "freezed out"
whilst radiation dominates (stangexpantion). As shown
schematically in Fig. 6, this "flattens" the
variance  M
at scales smaller than MH,eq; in fact,
M
at scales smaller than MH,eq; in fact,
 M
M
 ln(M)
at these scales, corresponding to galaxies! After teq
the CDM variance
(or power spectrum) grows at the same rate at all scales. If perturbations
are made out of baryons, then for scales smaller than
Ms, the gravito-acoustic
oscillations are damped out, while for scales close to the Hubble radius at
recombination, these oscillations are present. The "final" processed
mass variance or power spectrum is defined at the recombination epoch.
For example, the power spectrum is expressed as:
ln(M)
at these scales, corresponding to galaxies! After teq
the CDM variance
(or power spectrum) grows at the same rate at all scales. If perturbations
are made out of baryons, then for scales smaller than
Ms, the gravito-acoustic
oscillations are damped out, while for scales close to the Hubble radius at
recombination, these oscillations are present. The "final" processed
mass variance or power spectrum is defined at the recombination epoch.
For example, the power spectrum is expressed as:
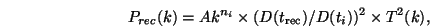 |
(10) |
where the first term is the initial power spectrum Pi(k); the second one is how much the fluctuation amplitude has grown in the linear regime (D(t) is the so-called linear growth factor), and the third one is a transfer function that encapsulates the different damping and freezing out processes able to deform the initial power spectrum shape. At large scales, T2(k) = 1, i.e. the primordial shape is conserved (see Fig. 6).
Besides the mass power spectrum, it is possible to calculate the
angular power spectrum of temperature fluctuation in the
CMBR. This spectrum consists basically of 2 ranges divided by a
critical angular scales:
the angle  h
corresponding to the horizon scale at the epoch of recombination
((LH)rec
h
corresponding to the horizon scale at the epoch of recombination
((LH)rec
 200(
200( h2)-1/2 Mpc, comoving). For scales grander
than
h2)-1/2 Mpc, comoving). For scales grander
than  h the
spectrum is featureless and corresponds to the scale-invariant
supra-horizon Sachs-Wolfe fluctuations. For scales smaller than
h the
spectrum is featureless and corresponds to the scale-invariant
supra-horizon Sachs-Wolfe fluctuations. For scales smaller than
 h,
the sub-horizon fluctuations are dominated by the Doppler scattering
(produced by the gravito-acoustic oscillations) with a series of decreasing
in amplitude peaks; the position (angle) of the first Doppler peak
depends strongly on
h,
the sub-horizon fluctuations are dominated by the Doppler scattering
(produced by the gravito-acoustic oscillations) with a series of decreasing
in amplitude peaks; the position (angle) of the first Doppler peak
depends strongly on  ,
i.e. on the geometry of the Universe.
In the last 15 years, high-technology experiments as COBE,
Boomerang, WMAP provided valuable information (in particular
the latter one) on CMBR anisotropies. The results of this exciting
branch of astronomy (called sometimes anisotronomy) were of paramount
importance for astronomy and cosmology (see for a review
[62]
and the W. Hu website
10).
,
i.e. on the geometry of the Universe.
In the last 15 years, high-technology experiments as COBE,
Boomerang, WMAP provided valuable information (in particular
the latter one) on CMBR anisotropies. The results of this exciting
branch of astronomy (called sometimes anisotronomy) were of paramount
importance for astronomy and cosmology (see for a review
[62]
and the W. Hu website
10).
Just to highlight some of the key results of CMBR studies, let us
mention the next ones: 1) detailed predictions of the
 CDM scenario
concerning the linear evolution of perturbations were accurately proved, 2)
several cosmological parameters as the geometry of the Universe, the
baryonic fraction
CDM scenario
concerning the linear evolution of perturbations were accurately proved, 2)
several cosmological parameters as the geometry of the Universe, the
baryonic fraction
 B, and
the index of the primordial power spectrum, were determined
with high precision (see the actualized, recently delivered results
from the 3 year analysis of WMAP in
[109]),
3) by studying
the polarization maps of the CMBR it was possible to infer the epoch when
the Universe started to be significantly reionized by the formation of
first stars, 4) the amplitude (normalization) of the primordial fluctuation
power spectrum was accurately measured. The latter
is crucial for further calculating the non-linear regime of cosmic structure
formation. I should emphasize that while the shape of the power spectrum is
predicted and well understood within the context of the
B, and
the index of the primordial power spectrum, were determined
with high precision (see the actualized, recently delivered results
from the 3 year analysis of WMAP in
[109]),
3) by studying
the polarization maps of the CMBR it was possible to infer the epoch when
the Universe started to be significantly reionized by the formation of
first stars, 4) the amplitude (normalization) of the primordial fluctuation
power spectrum was accurately measured. The latter
is crucial for further calculating the non-linear regime of cosmic structure
formation. I should emphasize that while the shape of the power spectrum is
predicted and well understood within the context of the
 CDM model, the
situation is fuzzy concerning the power spectrum normalization. We have a
phenomenological value for A but not a theoretical prediction.
CDM model, the
situation is fuzzy concerning the power spectrum normalization. We have a
phenomenological value for A but not a theoretical prediction.
4 It is well known that the name of 'Big Bang' is not appropriate for this theory. The key physical conditions required for an explosion are temperature and pressure gradients. These conditions contradict the Cosmological Principle of homogeneity and isotropy on which is based the 'Big Bang' theory. Back.
5 In the
1970s Y. Zel'dovich and collaborators worked out a scenario of galaxy
formation starting from very large perturbations, those that were not
affected by Silk damping. In this elegant scenario,
the large-scale perturbations, considered in a first approximation
as ellipsoids, collapse most rapidly along their shortest axis, forming
flattened structures ("pancakes"), which then fragment into galaxies
by gravitational or thermal instabilities. In this 'top-down' scenario,
to obtain galaxies in place at z~ 1, the amplitude of the
large perturbations at recombination should be
 3 × 10-3.
Observations of the CMBR anisotropies showed that the amplitudes are
1-2 order of magnitudes smaller than those required.
Back.
3 × 10-3.
Observations of the CMBR anisotropies showed that the amplitudes are
1-2 order of magnitudes smaller than those required.
Back.
6 The
reference to "early" and "late" is given by the epoch and the corresponding
radiation temperature when the largest galaxy-sized perturbations
(M ~ 1013
M ) enter the
horizon: agal ~ aeq
) enter the
horizon: agal ~ aeq
 1/3.9
× 104(
1/3.9
× 104( 0 h2) and Tr
~ 1 KeV.
Back.
0 h2) and Tr
~ 1 KeV.
Back.
7 Neutrinos exist and
have masses larger than 0.05 eV according to determinations based on solar
neutrino oscillations. Therefore, neutrinos contribute to the matter
density in the Universe. Cosmological observations
set a limit: 
 h2 < 0.0076, otherwise too much
structure is erased.
Back.
h2 < 0.0076, otherwise too much
structure is erased.
Back.
8 http://www.cmbfast.org and http://camb.info/ Back.
9 The phases of the Fourier modes in the Gaussian case are uncorrelated. Gaussianity is the simplest assumption for the primordial fluctuation field statistics and it seems to be consistent with some variants of inflation. However, there are other variants that predict non-Gaussian fluctuations (for a recent review on this subject see e.g. [8]), and the observational determination of the primordial fluctuation statistics is currently an active field of investigation. The properties of cosmic structures depend on the assumption about the primordial statistics, not only at large scales but also at galaxy scales; see for a review and new results [4]. Back.
10 http://background.uchicago.edu/~whu/physics/physics.html Back.