5. THE BRIGHT SIDE OF GALAXY FORMATION AND EVOLUTION

The CDM scenario of cosmic structure formation has been well tested for perturbations that are still in the linear or quasilinear phase of evolution. These tests are based, among other cosmological probes, on accurate measurements of:

• the CMBR temperature fluctuations at large and small angular scales

• the large-scale mass power spectrum as traced by the spatial distribution of galaxies and cluster of galaxies, by the Ly forest clouds, by maps of gravitational weak and strong lensing, etc.

• the peculiar large-scale motions of galaxies ¹³.

• the statistics of strong gravitational lensing (multiple-lensed arcs).

Although these cosmological probes are based on observations of luminous (baryonic) objects, the physics of baryons plays a minor or indirect role in the properties of the linear mass perturbations. The situation is different at small (galaxy) scales, where perturbations went into the non-linear regime and the dissipative physics of baryons becomes relevant. The interplay of DM and baryonic processes is crucial for understanding galaxy formation and evolution. The progress in this field was mostly heuristic; the CDM scenario provides the initial and boundary conditions for modeling galaxy evolution, but the complex physics of the baryonic processes, in the absence of fundamental theories, requires a model adjustment through confrontation with the observations.

Following, I will outline some key concepts, ingredients, and results of the galaxy evolution study based on the CDM scenario. Some of the pioneer papers in this field are those of Gunn [57], White & Reese [131], Fall & Efstathiou [43], Blumental et al. [15], Davis et al. [36], Katz & Gunn [65], White & Frenk [130], Kauffmann et al. [66]. For useful lecture notes and recent reviews see e.g., Longair [76, 77], White [129], Steinmetz [113], Firmani & Avila-Reese [46].

The main methods of studying galaxy formation and evolution in the CDM context are:

• Semi-analytical Models (e.g., [130, 66, 28, 9, 108, 29, 12, 10]), where the halo mass assembling histories are calculated with the extended Press-Schechter formalism and galaxies are seeded within the halos by means of phenomenological recipes. This method is very useful for producing whole populations of galaxies at a given epoch and predicting statistical properties as the luminosity function and the morphological mix.

• Semi-numerical Models (e.g, [45, 2, 119, 16]), where the internal physics of the galaxies, including those of the halos, are modeled numerically but under simplifying assumptions; the initial and boundary conditions are taken from the CDM scenario by using the extended Press-Schechter formalism and halo AM distributions from simulations. This method is useful to predict the local properties of galaxies and correlations among the global properties, as well as to follow the overall evolution of individual galaxies.

• Numerical N-body+hydrodyamical simulations (e.g., [65, 26, 64, 86, 112, 126, 1, 110, 56]), where the DM and baryonic processes are followed in cosmological simulations. This is the most advanced and complete approach to galaxy evolution. However, current limitations in the computational capabilities and the lack of fundamental theories for several of the physical processes involved, do not allow yet to exploit optimally this method. A great advance is being made currently with an hybrid approach: in the high-resolution cosmological N-body simulations of only DM, galaxies are grafted by using the semi-analytical models (e.g., [67, 60, 38, 13, 111, 63]).

5.1. Disks

The formation of galaxy disks deep inside the CDM halos is a generic process in the CDM scenario. Let us outline the (simplified) steps of disk galaxy formation in this scenario:

1. DM halo growth. The "mold" for disk formation is provided by the mass and AM distributions of the virialized halo, which grows hierarchically. A description of these aspects were presented in the previous Section.

2. Gas cooling and infall, and the maximum mass of galaxies. It is common to assume that the gas in a halo is shock-heated during collapse to the virial temperature [131]. The gas then cools radiatively and falls in a free-fall time to the center. The cooling function (n, T_k; Z) depends on the gas density, temperature, and composition ¹⁴. Since the seminal work by White & Frenk (1990) [130], the rate infall of gas available to form the galaxy is assumed to be driven either by the free-fall time, t_ff, if t_ff > t_cool or by the cooling time t_cool if t_ff < t_cool. The former case applies to halos of masses smaller than approximately 5 × 10¹¹ M, whilst the latter applies to more massive halos. The cooling flow from the quasistatic hot atmosphere is the process that basically limits the baryonic mass of galaxies [105], and therefore the bright end of the galaxy luminosity function; for the outer, dilute hot gas in large halos, t_cool becomes larger than the Hubble time. However, detailed calculations show that even so, in massive halos too much gas cools, and the bright end of the predicted luminosity function results with a decrease slower than the observed one [12]. Below we will see some solutions proposed to this problem.

More recently it was shown that the cooling of gas trapped in filaments during the halo collapse may be so rapid that the gas flows along the filaments to the center, thus avoiding shock heating [69]. However, this process is efficient only for halos less massive than 2.5 × 10¹¹ M, which in any case (even if shock-heating happens), cool their gas very rapidly [19]. Thus, for modeling the formation of disks, and for masses smaller than ~ 5 × 10¹¹ M, we may assume that gas infalls in a dynamical time since the halo has virialized, or in two dynamical times since the protostructure was at its maximum expansion.

3. Disk formation, the origin of exponentially, and rotation curves. The gas, originally distributed in mass and AM as the DM, cools and collapses until it reaches centrifugal balance in a disk. Therefore, assuming detailed AM conservation, the radial mass distribution of the disk can be calculated by equating its specific AM to the AM of its final circular orbit in centrifugal equilibrium. The typical collapse factor of the gas within a DM halo is ~ 10 - 15 ¹⁵, depending on the initial halo spin parameter ; the higher the , the more extended (lower surface density) is the resulting disk. The surface density profile of the disks formed within CDM halos is nearly exponential, which provides an explanation to the long-standing question of why galaxy disks are exponential. This is a direct consequence of the AM distribution acquired by the halos by tidal torques and mergers. In more detail, however, the profiles are more concentrated in the center and with a slight excess in the periphery than the exponential law [45, 22]. The cusp in the central disk could give rise to either a photometrical bulge [120] or to a real kinematical bulge due to disk gravitational instability enhanced by the higher central surface density [2] (bulge secular formation). In a few cases (high-, low-concentrated halos), purely exponential disks can be formed.

Baryons are a small mass fraction in the CDM halos, however, the disk formed in the center is very dense (recall the high collapse factors), so that the contribution of the baryonic disk to the inner gravitational potential is important or even dominant. The formed disk will drag gravitationally DM, producing an inner halo contraction that is important to calculate for obtaining the rotation curve decomposition. The method commonly used to calculate it is based on the approximation of radial adiabatic invariance, where spherical symmetry and circular orbits are assumed (e.g., [47, 82]). However, the orbits in CDM halos obtained in N-body simulations are elliptical rather than circular; by generalizing the adiabatic invariance to elliptical orbits, the halo contraction becomes less efficient [132, 52].

The rotation curve decomposition of disks within contracted CDM halos are in general consistent with observations [82, 45, 132] (nearly-flat total rotation curves; maximum disk for high-surface brightness disks; submaximum disk for the LSB disks; in more detail, the outer rotation curve shape depends on surface density, going from decreasing to increasing at the disk radius for higher to lower densities, respectively). However, there are important non-solved issues. For example, from a large sample of observed rotation curves, Persic et al. [95] inferred that the rotation curve shapes are described by an "universal" profile that (i) depends on the galaxy luminosity and (ii) implies a halo profile different from the CDM (NFW) profile. Other studies confirm only partially these claims [123, 132, 25]. Statistical studies of rotation curves are very important for testing the CDM scenario.

In general, the structure and dynamics of disks formed within CDM halos under the assumption of detailed AM conservation seem to be consistent with observations. An important result to remark is the successful prediction of the infrared Tully-Fisher relation and its scatter ¹⁶. The core problem mentioned in Section 4.2 is the most serious potential difficulty. Other potential difficulties are: (i) the predicted disk size (surface brightness) distribution implies a P() distribution narrower than that corresponding to CDM halos by almost a factor of two [74]; (ii) the internal AM distribution inferred from observations of dwarf galaxies seems not to be in agreement with the CDM halo AM distribution [122]; (iii) the inference of the halo profile from the statistical study of rotation curve shapes seems not to be agreement with CMD halos. In N-body+hydrodynamical simulations of disk galaxy formation there was common another difficulty called the 'angular momentum catastrophe': the simulated disks ended too much concentrated, apparently due to AM transference of baryons to DM during the gas collapse. The formation of highly concentrated disks also affects the shape of the rotation curve (strongly decreasing), as well as the zero-point of the Tully-Fisher relation. Recent numerical simulations are showing that the 'angular momentum catastrophe', rather than a physical problem, is a problem related to the resolution of the simulations and the correct inclusion of feedback effects.

4. Star formation and feedback. We are coming to the less understood and most complicated aspects of the models of galaxy evolution, which deserve separate notes. The star formation (SF) process is studied at two levels (each one by two separated communities!): (i) the small-scale physics, related to the complex processes by which the cold gas inside molecular clouds fragments and collapses into stars, and (ii) the large-scale physics, related to the disk global instabilities that give rise to the largest unities of SF, the molecular clouds. The SF physics incorporated to galaxy evolution models is still oversimplified, phenomenological and refers to the latter item. The large-scale SF cycle in normal galaxies is believed to be self-regulated by a balance between the energy injection due to SF (mainly SNe) and dissipation (radiative or turbulent). Two main approaches have been used to describe the SF self-regulation in models of galaxy evolution: (a) the halo cooling-feedback approach [130]), (b) the disk turbulent ISM approach [44, 124].

According to the former, the cool gas is reheated by the "galaxy" SF feedback and driven back to the intrahalo medium until it again cools radiatively and collapses into the galaxy. This approach has been used in semi-analytical models of galaxy formation where the internal structure and hydrodynamics of the disks are not treated in detail. The reheating rate is assumed to depend on the halo circular velocity V_c: _{rh s} / V_c, where _s is the SF rate (SFR) and 2. Thus, the galaxy SFR, gas fraction and luminosity depend on V_c. In these models, the disk ISM is virtually ignored and the SN-energy injection is assumed to be as efficient as to reheat the cold gas up to the virial temperature of the halo. A drawback of the model is that it predicts hot X-ray halos around disk galaxies much more luminous than those observed.

Approach (b) is more appropriate for models where the internal processes of the disk are considered. In this approach, the SF at a given radius r is assumed to be triggered by disk gravitational instabilities (Toomre criterion) and self-regulated by a balance between energy injection (mainly by SNe) and dissipation in the turbulent ISM in the direction perpendicular to the disk plane:

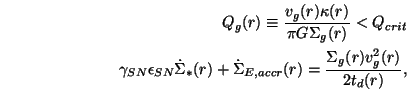(15) (16)

where v_g and _g are the gas velocity dispersion and surface density, is the epicyclic frequency, Q_crit is a critical value for instability, _SN and _SN are the kinetic energy injection efficiency of the SN into the gas and the SN energy generated per gram of gas transformed into stars, respectively, 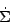_* is the surface SFR, and 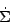_E,accr is the kinetic energy input due to mass accretion rate (or eventually any other energy source as AGN feedback). The key parameter in the self-regulating process is the dissipation time t_d. The disk ISM is a turbulent, non-isothermal, multi-temperature flow. Turbulent dissipation in the ISM is typically efficient (t_d ~ 10⁷ - 10⁸yr) in such a way that self-regulation happens at the characteristic vertical scales of the disk. Thus, there is not too much room for strong feedback with the gas at heights larger than the vertical scaleheigth of normal present-day disks: self-regulation is at the level of the disk, but not at the level of the gas corona around. With this approach the predicted SFR is proportional to _gⁿ (Schmidt law), with n 1.4 - 2 varying along the disk, in good agreement with observational inferences. The typical SF timescales are not longer than 3 - 4 Gyr. Therefore, to keep active SFRs in the disks, gas infall is necessary, a condition perfectly fulfilled in the CDM scenario.

Given the SFR radius by radius and time by time, and assuming an IMF, the corresponding luminosities in different color bands can be calculated with stellar population synthesis models. The final result is then an evolving inside-out luminous disk with defined global and local colors.

5. Secular evolution The "quiet" evolution of galaxy disks as described above can be disturbed by minor mergers (satellite accretion) and interactions with close galaxy companions. However, as several studies have shown, the disk may suffer even intrinsic instabilities which lead to secular changes in its structure, dynamics, and SFR. The main effects of secular evolution, i.e. dynamical processes that act in a timescale longer than the disk dynamical time, are the vertical thickening and "heating" of the disk, the formation of bars, which are efficient mechanisms of radial AM and mass redistribution, and the possible formation of (pseudo)bulges (see for recent reviews [71, 33]). Models of disk galaxy evolution should include these processes, which also can affect disk properties, for example increasing the disk scale radii [117].

5.2. Spheroids

As mentioned in Section 2, the simple appearance, the dominant old stellar populations, the -elements enhancement, and the dynamically hot structure of spheroids suggest that they were formed by an early (z 4) single violent event with a strong burst of star formation, followed by passive evolution of their stellar population (monolithic mechanism). Nevertheless, both observations and theory point out to a more complex situation. There are two ways to define the formation epoch of a spheroid: when most of its stars formed or when the stellar spheroid acquired its dynamical properties in violent or secular processes. For the monolithic collapse mechanism both epochs coincide.

In the context of the CDM scenario, spheroids are expected to be formed basically as the result of major mergers of disks. However,

• if the major mergers occur at high redshifts, when the disks are mostly gaseous, then the situation is close to the monolithic collapse;

• if the major mergers occur at low redshifts, when the galaxies have already transformed a large fraction of their gas into stars, then the spheroids assemble by the "classical" dissipationless collision.

Besides, stellar disks may develop spheroids in their centers (bulges) by secular evolution mechanisms, both intrinsic or enhanced by minor mergers and interactions; this channel of spheroid formation should work for late-type galaxies and it is supported by a large body of observations [71]. But the picture is even more complex in the hierarchical cosmogony as galaxy morphology may be continuously changing, depending on the MAH (smooth accretion and violent mergers) and environment. An spheroid formed early should continue accreting gas so that a new, younger disk grows around. A naive expectation in the context of the CDM scenario is that massive elliptical galaxies should be assembled mainly by late major mergers of the smaller galaxies in the hierarchy. It is also expected that the disks in galaxies with small bulge-to-disk ratios should be on average redder than those in galaxies with large bulge-to-disk ratios, contrary to observations.

Although it is currently subject of debate, a more elaborate picture of spheroid formation is emerging now in the context of the CDM hierarchical scenario (see [106, 46, 39] and the references therein). The basic ideas are that massive ellipticals formed early (z 3) and in a short timescale by the merging of gas-rich disks in rare high-peak, clustered regions of the Universe. The complex physics of the merging implies (i) an ultraluminous burst of SF obscured by dust (cool ULIRG phase) and the establishment of a spheroidal structure, (ii) gas collapse to the center, a situation that favors the growth of the preexisting massive black hole(s) through an Eddington or even super-Eddington regime (warm ULIRG phase), (iii) the switch on of the AGN activity associated to the supermassive black hole when reaching a critical mass, reverting then the gas inflow to gas outflow (QSO phase), (iv) the switch off of the AGN activity leaving a giant stellar spheroid with a supermassive black hole in the center and a hot gas corona around (passive elliptical evolution). In principle, the hot corona may cool by cooling flows and increase the mass of the galaxy, likely renewing a disk around the spheroid. However, it seems that recurrent AGN phases (less energetic than the initial QSO phase) are possible during the life of the spheroid. Therefore, the energy injected from AGN in the form of radio jets (feedback) can be responsible for avoiding the cooling flow. This way is solved the problem of disk formation around the elliptical, as well as the problem of the extended bright end in the luminosity function. It is also important to note that as soon as the halo hosting the elliptical becomes a subhalo of the group or cluster, the MAH is truncated (Section 4). According to the model just described, massive elliptical galaxies were in place at high redshifts, while less massive galaxies (collapsing from more common density peaks) assembled later. This model was called downsizing or anti-hierarchical. In spite of the name, it fits perfectly within the hierarchical CDM scenario.

5.3. Drivers of the Hubble sequence

• Disks are generic objects formed by gas dissipation and collapse inside the growing CDM halos. Three (cosmological) initial and boundary conditions related to the halos define the main properties of disks in isolated halos:

1. The virial mass, which determines extensive properties

2. The spin parameter , which determines mainly the disk surface brightness (SB; it gives rise to the sequence from high SB to low SB disks) and strongly influences the rotation curve shape and the bulge-to-disk ratio (within the secular scenario). also plays some role in the SFR history.

3. The MAH, which drives the gas infall rate and, therefore, the disk SFR and color; the MAH determines also the halo concentration, and its scatter is reflected in the scatter of the Tully-Fisher relation.

The two latter determine the intensive properties of disks, suggesting a biparametrical sequence in SB and color. There is a fourth important parameter, the galaxy baryon fraction f_B, which influences the disk SB and rotation curve shape. We have seen that f_B in galaxies is 3-5 times lower than the universal _B / _DM fraction. This parameter is related probably to astrophysical processes as gas dissipation and feedback.

• The clustering of CDM halos follows an spatial distribution with very different large-scale environments. In low-density environments, halos live mostly isolated, favoring the formation of disks, whose properties are driven by the factors mentioned above. However, as we move to higher-density environments, halos form from more and more clustered high-peak perturbations that assemble early by violent major mergers: this is the necessary condition to form massive ellipticals. At some time, the larger scale in the hierarchy collapses and the halo becomes a subhalo: the mass aggregation is then truncated and the probability of merging decreases dramatically. Elliptical galaxies are settled and continue evolving passively. Thus, the environment of CDM halos is another important driver of the Hubble sequence, able to establish the main body of the observed blue-red and early-type morphology sequences and their dependences on density.

• Although the initial, boundary and environmental conditions provided by the CDM scenario are drivers of several of the main properties and correlations of galaxies, astrophysical processes should also play an important role. The driving astrophysical processes are global SF and feedback. They should come in two modes that drive the disk and elliptical sequences: (i) the quiescent disk mode, where disk instabilities trigger SF and local (negative) feedback self-regulates the SFR, and (ii) the bursting mode of violent mergers of gaseous galaxies, where local shocks and gravothermal catastrophe trigger SF, and presumably a positive feedback increases its efficiency. Other important astrophysical drivers of galaxy properties are: (i) the SN-induced wind-driven outflows, which are important to shape the properties of dwarf galaxies (M 10¹⁰ M, V_m 80 km/s), (ii) the AGN-induced hydrodynamical outflows, which are important to prevent cooling flows in massive ellipticals, (iii) several processes typical of high-density environments such as ram pressure, harassment, strangulation, etc., presumably important to shape some properties of galaxies in clusters.

¹³ Recall that linear theory relates the peculiar velocity, that is the velocity deviation from the Hubble flow, to the density contrast. It is said that the cosmological velocity field is potential; any primordial rotational motion able to give rise to a density perturbation decays as the Universe expands due to angular momentum conservation. Back.

¹⁴ The main cooling processes for the intrahalo gas are collisional excitation and ionization, recombination, and bremsstrahlung. The former is the most efficient for kinetic temperatures T_k 10⁴ - 10⁵ K and for neutral hydrogen and single ionized helium; for a meta-enriched gas, cooling is efficient at temperatures between 10⁵ - 10⁷ K. At higher temperatures, where the gas is completely ionized, the dominant cooling process is bremsstrahlung. At temperatures lower than 10⁴ K (small halos) and in absence of metals, the main cooling process is by H₂ and HD molecule line emission. Back.

¹⁵ It is interesting to note that in the absence of a massive halo around galaxies, the collapse factor would be larger by ~ M / M_d 20, where M and M_d are the total halo and disk masses, respectively [90]. Back.

¹⁶ In Section 4.1 we have shown that the basis of the Tully-Fisher relation is the CDM halo M - V_m relation. From the pure halo to the disk+halo system there are several intermediate processes that could distort the original M - V_m relation. However, it was shown that the way in which the CDM halo couples with the disk and the way galaxies transform their gas into stars "conspire" to keep the relation. Due to this conspiring, the Tully-Fisher relation is robust to variations in the baryon fraction f_B (or mass-to-luminosity ratios) and in the spin parameter [45]. Back.