6. SUPERMASSIVE BLACK HOLES

6.1. The Principle of Self-Regulation

The fossil record in the present-day Universe indicates that every bulged galaxy hosts a supermassive black hole (BH) at its center [206]. This conclusion is derived from a variety of techniques which probe the dynamics of stars and gas in galactic nuclei. The inferred BHs are dormant or faint most of the time, but ocassionally flash in a short burst of radiation that lasts for a small fraction of the Hubble time. The short duty cycle acounts for the fact that bright quasars are much less abundant than their host galaxies, but it begs the more fundamental question: why is the quasar activity so brief? A natural explanation is that quasars are suicidal, namely the energy output from the BHs regulates their own growth.

Supermassive BHs make up a small fraction, < 10^-3, of the total mass in their host galaxies, and so their direct dynamical impact is limited to the central star distribution where their gravitational influence dominates. Dynamical friction on the background stars keeps the BH close to the center. Random fluctuations in the distribution of stars induces a Brownian motion of the BH. This motion can be decribed by the same Langevin equation that captures the motion of a massive dust particle as it responds to random kicks from the much lighter molecules of air around it [86]. The characteristic speed by which the BH wanders around the center is small, ~ (m_* / M_BH)^1/2 _*, where m_* and M_BH are the masses of a single star and the BH, respectively, and _* is the stellar velocity dispersion. Since the random force fluctuates on a dynamical time, the BH wanders across a region that is smaller by a factor of ~ (m_* / M_BH)^1/2 than the region traversed by the stars inducing the fluctuating force on it.

The dynamical insignificance of the BH on the global galactic scale is misleading. The gravitational binding energy per rest-mass energy of galaxies is of order ~ (_* / c)² < 10^-6. Since BH are relativistic objects, the gravitational binding energy of material that feeds them amounts to a substantial fraction its rest mass energy. Even if the BH mass occupies a fraction as small as ~ 10^-4 of the baryonic mass in a galaxy, and only a percent of the accreted rest-mass energy leaks into the gaseous environment of the BH, this slight leakage can unbind the entire gas reservoir of the host galaxy! This order-of-magnitude estimate explains why quasars are short lived. As soon as the central BH accretes large quantities of gas so as to significantly increase its mass, it releases large amounts of energy that would suppress further accretion onto it. In short, the BH growth is self-regulated.

The principle of self-regulation naturally leads to a correlation between the final BH mass, M_bh, and the depth of the gravitational potential well to which the surrounding gas is confined which can be characterized by the velocity dispersion of the associated stars, ~ _*². Indeed such a correlation is observed in the present-day Universe [368]. The observed power-law relation between M_bh and _* can be generalized to a correlation between the BH mass and the circular velocity of the host halo, v_c [130], which in turn can be related to the halo mass, M_halo, and redshift, z [394]

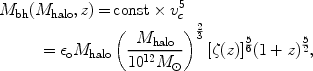(113)

where _o 10^-5.7 is a constant, and as before [(_m / _m^z)(_c / 18²)], _m^z [1 + ( / _m)(1 + z)^-3]^-1, _c = 18² + 82d - 39d², and d = _m^z - 1. If quasars shine near their Eddington limit as suggested by observations of low and high-redshift quasars [134, 384], then the above value of _o implies that a fraction of ~ 5 - 10% of the energy released by the quasar over a galactic dynamical time needs to be captured in the surrounding galactic gas in order for the BH growth to be self-regulated [394].

With this interpretation, the M_bh - _* relation reflects the limit introduced to the BH mass by self-regulation; deviations from this relation are inevitable during episodes of BH growth or as a result of mergers of galaxies that have no cold gas in them. A physical scatter around this upper envelope could also result from variations in the efficiency by which the released BH energy couples to the surrounding gas.

Various prescriptions for self-regulation were sketched by Silk & Rees [339]. These involve either energy or momentum-driven winds, where the latter type is a factor of ~ v_c / c less efficient [35, 199, 262]. Wyithe & Loeb [394] demonstrated that a particularly simple prescription for an energy-driven wind can reproduce the luminosity function of quasars out to highest measured redshift, z ~ 6 (see Figs. 38 and 40), as well as the observed clustering properties of quasars at z ~ 3 [398] (see Fig. 41). The prescription postulates that: (i) self-regulation leads to the growth of M_bh up the redshift-independent limit as a function of v_c in Eq. (113), for all galaxies throughout their evolution; and (ii) the growth of M_bh to the limiting mass in Eq. (113) occurs through halo merger episodes during which the BH shines at its Eddington luminosity (with the median quasar spectrum) over the dynamical time of its host galaxy, t_dyn. This model has only one adjustable parameter, namely the fraction of the released quasar energy that couples to the surrounding gas in the host galaxy. This parameter can be fixed based on the M_bh - _* relation in the local Universe [130]. It is remarkable that the combination of the above simple prescription and the standard CDM cosmology for the evolution and merger rate of galaxy halos, lead to a satisfactory agreement with the rich data set on quasar evolution over cosmic history.

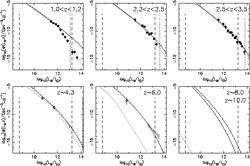Figure 38. Comparison of the observed and model luminosity functions (from [394]). The data points at z < 4 are summarized in Ref. [286], while the light lines show the double power-law fit to the 2dF quasar luminosity function [56]. At z ~ 4.3 and z ~ 6.0 the data is from Refs. [125]. The grey regions show the 1 - range of logarithmic slope ([-2.25,-3.75] at z ~ 4.3 and [-1.6,-3.1] at z ~ 6), and the vertical bars show the uncertainty in the normalization. The open circles show data points converted from the X-ray luminosity function [20] of low luminosity quasars using the median quasar spectral energy distribution. In each panel the vertical dashed lines correspond to the Eddington luminosities of BHs bracketing the observed range of the Mbh - vc relation, and the vertical dotted line corresponds to a BH in a 1013.5 M galaxy.

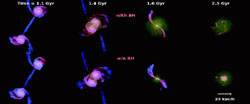Figure 39. Simulation images of a merger of galaxies resulting in quasar activity that eventually shuts-off the accretion of gas onto the black hole (from Di Matteo et al. 2005 [108]). The upper (lower) panels show a sequence of snapshots of the gas distribution during a merger with (without) feedback from a central black hole. The temperature of the gas is color coded.

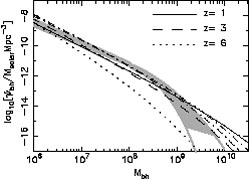Figure 40. The comoving density of supermassive BHs per unit BH mass (from [394]). The grey region shows the estimate based on the observed velocity distribution function of galaxies in Ref. [336] and the Mbh - vc relation in Eq. (113). The lower bound corresponds to the lower limit in density for the observed velocity function while the grey lines show the extrapolation to lower densities. We also show the mass function computed at z = 1, 3 and 6 from the Press-Schechter [292] halo mass function and Eq. (113), as well as the mass function at z ~ 2.35 and z ~ 3 implied by the observed density of quasars and a quasar lifetime of order the dynamical time of the host galactic disk, tdyn (dot-dashed lines).

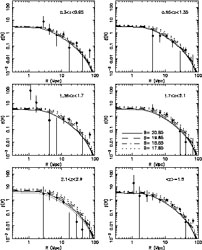Figure 41. Predicted correlation function of quasars at various redshifts in comparison to the 2dF data [101] (from [398]). The dark lines show the correlation function predictions for quasars of various apparent B-band magnitudes. The 2dF limit is B ~ 20.85. The lower right panel shows data from entire 2dF sample in comparison to the theoretical prediction at the mean quasar redshift of <z> = 1.5. The B = 20.85 prediction at this redshift is also shown by thick gray lines in the other panels to guide the eye. The predictions are based on the scaling Mbh vc5 in Eq. (113).

The cooling time of the heated gas is typically longer than its dynamical time and so the gas should expand into the galactic halo and escape the galaxy if its initial temperature exceeds the virial temperature of the galaxy [394]. The quasar remains active during the dynamical time of the initial gas reservoir, ~ 10⁷ years, and fades afterwards due to the dilution of this reservoir. Accretion is halted as soon as the quasar supplies the galactic gas with more than its binding energy. The BH growth may resume if the cold gas reservoir is replenished through a new merger.

Following the early analytic work, extensive numerical simulations by Springel, Hernquist, & Di Matteo (2005) [350] (see also Di Matteo et al. 2005 [108]) demonstrated that galaxy mergers do produce the observed correlations between black hole mass and spheroid properties when a similar energy feedback is incorporated. Because of the limited resolution near the galaxy nucleus, these simulations adopt a simple prescription for the accretion flow that feeds the black hole. The actual feedback in reality may depend crucially on the geometry of this flow and the physical mechanism that couples the energy or momentum output of the quasar to the surrounding gas.

Agreement between the predicted and observed correlation function of quasars (Fig. 41) is obtained only if the BH mass scales with redshift as in Eq. (113) and the quasar lifetime is of the order of the dynamical time of the host galactic disk [398],

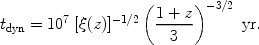(114)

This characterizes the timescale it takes low angular momentum gas to settle inwards and feed the black hole from across the galaxy before feedback sets in and suppresses additional infall. It also characterizes the timescale for establishing an outflow at the escape speed from the host spheroid.

The inflow of cold gas towards galaxy centers during the growth phase of the BH would naturally be accompanied by a burst of star formation. The fraction of gas that is not consumed by stars or ejected by supernovae, will continue to feed the BH. It is therefore not surprising that quasar and starburst activities co-exist in Ultra Luminous Infrared Galaxies [356], and that all quasars show broad metal lines indicating a super-solar metallicity of the surrounding gas [106]. Applying a similar self-regulation principle to the stars, leads to the expectation [394, 197] that the ratio between the mass of the BH and the mass in stars is independent of halo mass (as observed locally [243]) but increases with redshift as (z)^1/2(1 + z)^3/2. A consistent trend has indeed been inferred in an observed sample of gravitationally-lensed quasars [305].

The upper mass of galaxies may also be regulated by the energy output from quasar activity. This would account for the fact that cooling flows are suppressed in present-day X-ray clusters [123, 91, 273], and that massive BHs and stars in galactic bulges were already formed at z ~ 2. The quasars discovered by the Sloan Digital Sky Survey (SDSS) at z ~ 6 mark the early growth of the most massive BHs and galactic spheroids. The present-day abundance of galaxies capable of hosting BHs of mass ~ 10⁹ M (based on Eq. 113) already existed at z ~ 6 [225]. At some epoch, the quasar energy output may have led to the extinction of cold gas in these galaxies and the suppression of further star formation in them, leading to an apparent "anti-hierarchical" mode of galaxy formation where massive spheroids formed early and did not make new stars at late times. In the course of subsequent merger events, the cores of the most massive spheroids acquired an envelope of collisionless matter in the form of already-formed stars or dark matter [225], without the proportional accretion of cold gas into the central BH. The upper limit on the mass of the central BH and the mass of the spheroid is caused by the lack of cold gas and cooling flows in their X-ray halos. In the cores of cooling X-ray clusters, there is often an active central BH that supplies sufficient energy to compensate for the cooling of the gas [91, 123, 35]. The primary physical process by which this energy couples to the gas is still unknown.

6.2. Feedback on Large Intergalactic Scales

Aside from affecting their host galaxy, quasars disturb their large-scale cosmological environment. Powerful quasar outflows are observed in the form of radio jets [34] or broad-absorption-line winds [160]. The amount of energy carried by these outflows is largely unknown, but could be comparable to the radiative output from the same quasars. Furlanetto & Loeb [139] have calculated the intergalactic volume filled by such outflows as a function of cosmic time (see Fig. 42). This volume is likely to contain magnetic fields and metals, providing a natural source for the observed magnetization of the metal-rich gas in X-ray clusters [207] and in galaxies [103]. The injection of energy by quasar outflows may also explain the deficit of Ly absorption in the vicinity of Lyman-break galaxies [7, 100] and the required pre-heating in X-ray clusters [54, 91].

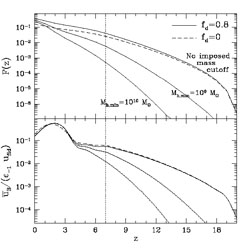Figure 42. The global influence of magnetized quasar outflows on the intergalactic medium (from [139]). Upper Panel: Predicted volume filling fraction of magnetized quasar bubbles F(z), as a function of redshift. Lower Panel: Ratio of normalized magnetic energy density, b / -1, to the fiducial thermal energy density of the intergalactic medium ufid = 3 n(z) k TIGM, where TIGM = 104 K, as a function of redshift (see [139] for more details). In each panel, the solid curves assume that the blast wave created by quasar ouflows is nearly (80%) adiabatic, and that the minimum halo mass of galaxies, Mh,min, is determined by atomic cooling before reionization and by suppression due to galactic infall afterwards (top curve), Mh,min = 109 M (middle curve), and Mh,min = 1010 M (bottom curve). The dashed curve assumes a fully-radiative blast wave and fixes Mh,min by the thresholds for atomic cooling and infall suppression. The vertical dotted line indicates the assumed redshift of complete reionization, zr = 7.

Beyond the reach of their outflows, the brightest SDSS quasars at z > 6 are inferred to have ionized exceedingly large regions of gas (tens of comoving Mpc) around them prior to global reionization (see Fig. 43 and Refs. [381, 400]). Thus, quasars must have suppressed the faint-end of the galaxy luminosity function in these regions before the same occurred throughout the Universe. The recombination time is comparable to the Hubble time for the mean gas density at z ~ 7 and so ionized regions persist [272] on these large scales where inhomogeneities are small. The minimum galaxy mass is increased by at least an order of magnitude to a virial temperature of ~ 10⁵ K in these ionized regions [23]. It would be particularly interesting to examine whether the faint end (_* < 30 km s^-1) of the luminosity function of dwarf galaxies shows any moduluation on large-scales around rare massive BHs, such as M87.

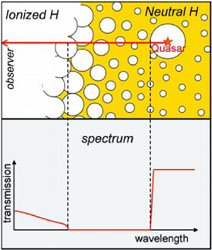Figure 43. Quasars serve as probes of the end of reionization. The measured size of the HII regions around SDSS quasars can be used [396, 251] to demonstrate that a significant fraction of the intergalactic hydrogen was neutral at z ~ 6.3 or else the inferred size of the quasar HII regions would have been much larger than observed (assuming typical quasar lifetimes [248]). Also, quasars can be used to measure the redshift at which the intergalactic medium started to transmit Ly photons [381, 400]. The upper panel illustrates how the line-of-sight towards a quasar intersects this transition redshift. The resulting Ly transmission of the intrinsic quasar spectrum is shown schematically in the lower panel.

To find the volume filling fraction of relic regions from z ~ 6, we consider a BH of mass M_bh ~ 3 × 10⁹ M. We can estimate the comoving density of BHs directly from the observed quasar luminosity function and our estimate of quasar lifetime. At z ~ 6, quasars powered by M_bh ~ 3 × 10⁹ M BHs had a comoving density of ~ 0.5G pc^-3 [394]. However, the Hubble time exceeds t_dyn by a factor of ~ 2 × 10² (reflecting the square root of the density contrast of cores of galaxies relative to the mean density of the Universe), so that the comoving density of the bubbles created by the z ~ 6 BHs is ~ 10²Gpc^-3 (see Fig. 40). The density implies that the volume filling fraction of relic z ~ 6 regions is small, < 10%, and that the nearest BH that had M_bh ~ 3 × 10⁹ M at z ~ 6 (and could have been detected as an SDSS quasar then) should be at a distance d_bh ~ (4 / 3 × 10²)^1/3 Gpc ~ 140 Mpc which is almost an order-of-magnitude larger than the distance of M87, a galaxy known to possess a BH of this mass [135].

What is the most massive BH that can be detected dynamically in a local galaxy redshift survey? SDSS probes a volume of ~ 1 Gpc³ out to a distance ~ 30 times that of M87. At the peak of quasar activity at z ~ 3, the density of the brightest quasars implies that there should be ~ 100 BHs with masses of 3 × 10¹⁰ M per Gpc³, the nearest of which will be at a distance d_bh ~ 130 Mpc, or ~ 7 times the distance to M87. The radius of gravitational influence of the BH scales as M_bh / v_c² M_bh^3/5. We find that for the nearest 3 × 10⁹ M and 3 × 10¹⁰ M BHs, the angular radius of influence should be similar. Thus, the dynamical signature of ~ 3 × 10¹⁰ M BHs on their stellar host should be detectable.

6.3. What seeded the growth of the supermassive black holes?

The BHs powering the bright SDSS quasars possess a mass of a few × 10⁹ M, and reside in galaxies with a velocity dispersion of ~ 500 km s^-1 [24]. A quasar radiating at its Eddington limiting luminosity, L_e = 1.4 × 10⁴⁶ erg s^-1(M_bh / 10⁸ M), with a radiative efficiency, _rad = L_e / c² would grow exponentially in mass as a function of time t, M_bh = M_seed exp{t / t_e} on a time scale, t_e = 4.1 × 10⁷ yr (_rad / 0.1). Thus, the required growth time in units of the Hubble time t_hubble = 9 × 10⁸ yr[(1 + z) / 7]^-3/2 is

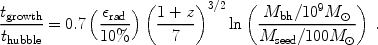(115)

The age of the Universe at z ~ 6 provides just sufficient time to grow an SDSS BH with M_bh ~ 10⁹ M out of a stellar mass seed with _rad = 10% [175]. The growth time is shorter for smaller radiative efficiencies, as expected if the seed originates from the optically-thick collapse of a supermassive star (in which case M_seed in the logarithmic factor is also larger).

What was the mass of the initial BH seeds? Were they planted in early dwarf galaxies through the collapse of massive, metal free (Pop-III) stars (leading to M_seed of hundreds of solar masses) or through the collapse of even more massive, i.e. supermassive, stars [220] ? Bromm & Loeb [63] have shown through a hydrodynamical simulation (see Fig. 44) that supermassive stars were likely to form in early galaxies at z ~ 10 in which the virial temperature was close to the cooling threshold of atomic hydrogen, ~ 10⁴ K. The gas in these galaxies condensed into massive ~ 10⁶ M clumps (the progenitors of supermassive stars), rather than fragmenting into many small clumps (the progenitors of stars), as it does in environments that are much hotter than the cooling threshold. This formation channel requires that a galaxy be close to its cooling threshold and immersed in a UV background that dissociates molecular hydrogen in it. These requirements should make this channel sufficiently rare, so as not to overproduce the cosmic mass density of supermassive BH.

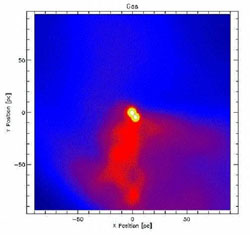Figure 44. SPH simulation of the collapse of an early dwarf galaxy with a virial temperature just above the cooling threshold of atomic hydrogen and no H2 (from [63]). The image shows a snapshot of the gas density distribution at z 10, indicating the formation of two compact objects near the center of the galaxy with masses of 2.2 × 106 M and 3.1 × 106 M, respectively, and radii < 1 pc. Sub-fragmentation into lower mass clumps is inhibited as long as molecular hydrogen is dissociated by a background UV flux. These circumstances lead to the formation of supermassive stars [220] that inevitably collapse and trigger the birth of supermassive black holes [220, 309]. The box size is 200 pc.

The minimum seed BH mass can be identified observationally through the detection of gravitational waves from BH binaries with Advanced LIGO [395] or with LISA [393]. Most of the mHz binary coalescence events originate at z > 7 if the earliest galaxies included BHs that obey the M_bh - v_c relation in Eq. (113). The number of LISA sources per unit redshift per year should drop substantially after reionization, when the minimum mass of galaxies increased due to photo-ionization heating of the intergalactic medium. Studies of the highest redshift sources among the few hundred detectable events per year, will provide unique information about the physics and history of BH growth in galaxies [327].

The early BH progenitors can also be detected as unresolved point sources, using the future James Webb Space Telescope (JWST). Unfortunately, the spectrum of metal-free massive and supermassive stars is the same, since their surface temperature ~ 10⁵ K is independent of mass [59]. Hence, an unresolved cluster of massive early stars would show the same spectrum as a supermassive star of the same total mass.

It is difficult to ignore the possible environmental impact of quasars on anthropic selection. One may wonder whether it is not a coincidence that our Milky-Way Galaxy has a relatively modest BH mass of only a few million solar masses in that the energy output from a much more massive (e.g. ~ 10⁹ M) black hole would have disrupted the evolution of life on our planet. A proper calculation remains to be done (as in the context of nearby Gamma-Ray Bursts [316]) in order to demonstrate any such link.