7. RADIATIVE FEEDBACK FROM THE FIRST SOURCES OF LIGHT

7.1. Escape of Ionizing Radiation from Galaxies

The intergalactic ionizing radiation field, a key ingredient in the development of reionization, is determined by the amount of ionizing radiation escaping from the host galaxies of stars and quasars. The value of the escape fraction as a function of redshift and galaxy mass remains a major uncertainty in all current studies, and could affect the cumulative radiation intensity by orders of magnitude at any given redshift. Gas within halos is far denser than the typical density of the IGM, and in general each halo is itself embedded within an overdense region, so the transfer of the ionizing radiation must be followed in the densest regions in the Universe. Reionization simulations are limited in resolution and often treat the sources of ionizing radiation and their immediate surroundings as unresolved point sources within the large-scale intergalactic medium (see, e.g., Gnedin 2000 [152]). The escape fraction is highly sensitive to the three-dimensional distribution of the UV sources relative to the geometry of the absorbing gas within the host galaxy (which may allow escape routes for photons along particular directions but not others).

The escape of ionizing radiation (h > 13.6 eV, < 912 Å) from the disks of present-day galaxies has been studied in recent years in the context of explaining the extensive diffuse ionized gas layers observed above the disk in the Milky Way [300] and other galaxies [295, 183]. Theoretical models predict that of order 3 - 14% of the ionizing luminosity from O and B stars escapes the Milky Way disk [111, 110]. A similar escape fraction of f_esc = 6% was determined by Bland-Hawthorn & Maloney (1999) [46] based on H measurements of the Magellanic Stream. From Hopkins Ultraviolet Telescope observations of four nearby starburst galaxies (Leitherer et al. 1995 [217]; Hurwitz, Jelinsky, & Dixon 1997 [185]), the escape fraction was estimated to be in the range 3% < f_esc < 57%. If similar escape fractions characterize high redshift galaxies, then stars could have provided a major fraction of the background radiation that reionized the IGM [236, 238]. However, the escape fraction from high-redshift galaxies, which formed when the Universe was much denser ( (1 + z)³), may be significantly lower than that predicted by models ment to describe present-day galaxies. Current reionization calculations assume that galaxies are isotropic point sources of ionizing radiation and adopt escape fractions in the range 5% < f_esc < 60% [152].

Clumping is known to have a significant effect on the penetration and escape of radiation from an inhomogeneous medium [49, 385, 269, 173, 42]. The inclusion of clumpiness introduces several unknown parameters into the calculation, such as the number and overdensity of the clumps, and the spatial correlation between the clumps and the ionizing sources. An additional complication may arise from hydrodynamic feedback, whereby part of the gas mass is expelled from the disk by stellar winds and supernovae (Section 8).

Wood & Loeb (2000) [387] used a three-dimensional radiation transfer code to calculate the steady-state escape fraction of ionizing photons from disk galaxies as a function of redshift and galaxy mass. The gaseous disks were assumed to be isothermal, with a sound speed c_s ~ 10 km s^-1, and radially exponential, with a scale-length based on the characteristic spin parameter and virial radius of their host halos. The corresponding temperature of ~ 10⁴ K is typical for a gas which is continuousely heated by photo-ionization from stars. The sources of radiation were taken to be either stars embedded in the disk, or a central quasar. For stellar sources, the predicted increase in the disk density with redshift resulted in a strong decline of the escape fraction with increasing redshift. The situation is different for a central quasar. Due to its higher luminosity and central location, the quasar tends to produce an ionization channel in the surrounding disk through which much of its ionizing radiation escapes from the host. In a steady state, only recombinations in this ionization channel must be balanced by ionizations, while for stars there are many ionization channels produced by individual star-forming regions and the total recombination rate in these channels is very high. Escape fractions > 10% were achieved for stars at z ~ 10 only if ~ 90% of the gas was expelled from the disks or if dense clumps removed the gas from the vast majority (> 80%) of the disk volume (see Fig. 45). This analysis applies only to halos with virial temperatures > 10⁴ K. Ricotti & Shull (2000) [302] reached similar conclusions but for a quasi-spherical configuration of stars and gas. They demonstrated that the escape fraction is substantially higher in low-mass halos with a virial temperature < 10⁴ K. However, the formation of stars in such halos depends on their uncertain ability to cool via the efficient production of molecular hydrogen.

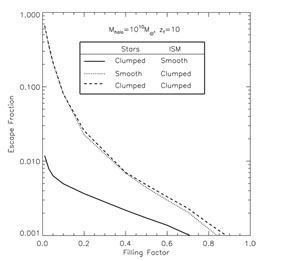Figure 45. Escape fractions of stellar ionizing photons from a gaseous disk embedded within a 1010 M halo which have formed at z = 10 (from Wood & Loeb 2000 [387]). The curves show three different cases of clumpiness within the disk. The volume filling factor refers to either the ionizing emissivity, the gas clumps, or both, depending on the case. The escape fraction is substantial (> 1%) only if the gas distribution is highly clumped.

The main uncertainty in the above predictions involves the distribution of the gas inside the host galaxy, as the gas is exposed to the radiation released by stars and the mechanical energy deposited by supernovae. Given the fundamental role played by the escape fraction, it is desirable to calibrate its value observationally. Steidel, Pettini, & Adelberger [352] reported a detection of significant Lyman continuum flux in the composite spectrum of 29 Lyman break galaxies (LBG) with redshifts in the range z = 3.40 ± 0.09. They co-added the spectra of these galaxies in order to be able to measure the low flux. Another difficulty in the measurement comes from the need to separate the Lyman-limit break caused by the interstellar medium from that already produced in the stellar atmospheres. After correcting for intergalactic absorption, Steidel et al. [352] inferred a ratio between the emergent flux density at 1500 Å and 900 Å (rest frame) of 4.6 ± 1.0. Taking into account the fact that the stellar spectrum should already have an intrinsic Lyman discontinuity of a factor of ~ 3 - 5, but that only ~ 15 - 20% of the 1500 Å photons escape from typical LBGs without being absorbed by dust (Pettini et al. 1998 [290]; Adelberger et al. 2000 [6]), the inferred 900 Å escape fraction is f_esc ~ 10 - 20%. Although the galaxies in this sample were drawn from the bluest quartile of the LBG spectral energy distributions, the measurement implies that this quartile may itself dominate the hydrogen-ionizing background relative to quasars at z ~ 3.

7.2. Propagation of Ionization Fronts in the IGM

The radiation output from the first stars ionizes hydrogen in a growing volume, eventually encompassing almost the entire IGM within a single H II bubble. In the early stages of this process, each galaxy produces a distinct H II region, and only when the overall H II filling factor becomes significant do neighboring bubbles begin to overlap in large numbers, ushering in the "overlap phase" of reionization. Thus, the first goal of a model of reionization is to describe the initial stage, when each source produces an isolated expanding H II region.

We assume a spherical ionized volume V, separated from the surrounding neutral gas by a sharp ionization front. Indeed, in the case of a stellar ionizing spectrum, most ionizing photons are just above the hydrogen ionization threshold of 13.6 eV, where the absorption cross-section is high and a very thin layer of neutral hydrogen is sufficient to absorb all the ionizing photons. On the other hand, an ionizing source such as a quasar produces significant numbers of higher energy photons and results in a thicker transition region.

In the absence of recombinations, each hydrogen atom in the IGM would only have to be ionized once, and the ionized proper volume V_p would simply be determined by

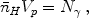(116)

where _H is the mean number density of hydrogen and N is the total number of ionizing photons produced by the source. However, the increased density of the IGM at high redshift implies that recombinations cannot be neglected. Indeed, in the case of a steady ionizing source (and neglecting the cosmological expansion), a steady-state volume would be reached corresponding to the Strömgren sphere, with recombinations balancing ionizations:

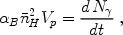(117)

where the recombination rate depends on the square of the density and on the case B recombination coefficient _b = 2.6 × 10^-13 cm³ s^-1 for hydrogen at T = 10⁴ K. The exact evolution for an expanding H II region, including a non-steady ionizing source, recombinations, and cosmological expansion, is given by (Shapiro & Giroux 1987 [329])

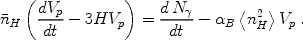(118)

In this equation, the mean density n_H varies with time as 1 / a³(t). A critical physical ingredient is the dependence of recombination on the square of the density. This means that if the IGM is not uniform, but instead the gas which is being ionized is mostly distributed in high-density clumps, then the recombination time is very short. This is often dealt with by introducing a volume-averaged clumping factor C (in general time-dependent), defined by ⁸

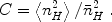(119)

If the ionized volume is large compared to the typical scale of clumping, so that many clumps are averaged over, then equation (118) can be solved by supplementing it with equation (119) and specifying C. Switching to the comoving volume V, the resulting equation is

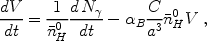(120)

where the present number density of hydrogen is

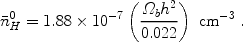(121)

This number density is lower than the total number density of baryons _b⁰ by a factor of ~ 0.76, corresponding to the primordial mass fraction of hydrogen. The solution for V(t) (generalized from Shapiro & Giroux 1987 [329]) around a source which turns on at t = t_i is

(122)

where

(123)

At high redshift (when (1 + z) >> |_m^-1 - 1|), the scale factor varies as

(124)

and with the additional assumption of a constant C the function F simplifies as follows. Defining

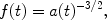(125)

we derive

(126)

where the last equality assumes C = 10 and our standard choice of cosmological parameters: _m = 0.3, = 0.7, and _b = 0.045. Although this expression for F(t', t) is in general an accurate approximation at high redshift, in the particular case of the CDM model (where _m + = 1) we get the exact result by replacing equation (125) with

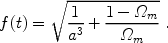(127)

The size of the resulting H II region depends on the halo which produces it. Consider a halo of total mass M and baryon fraction _b / _m. To derive a rough estimate, we assume that baryons are incorporated into stars with an efficiency of f_star = 10%, and that the escape fraction for the resulting ionizing radiation is also f_esc = 10%. If the stellar IMF is similar to the one measured locally [315], then N 4000 ionizing photons are produced per baryon in stars (for a metallicity equal to 1/20 of the solar value). We define a parameter which gives the overall number of ionizations per baryon,

(128)

If we neglect recombinations then we obtain the maximum comoving radius of the region which the halo of mass M can ionize,

(129)

for our standard set of parameters. The actual radius never reaches this size if the recombination time is shorter than the lifetime of the ionizing source. For an instantaneous starburst with the Scalo (1998) [315] IMF, the production rate of ionizing photons can be approximated as

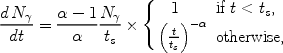(130)

where N = 4000, = 4.5, and the most massive stars fade away with the characteristic timescale t_s = 3 × 10⁶ yr. In figure 46 we show the time evolution of the volume ionized by such a source, with the volume shown in units of the maximum volume V_max which corresponds to r_max in equation (129). We consider a source turning on at z = 10 (solid curves) or z = 15 (dashed curves), with three cases for each: no recombinations, C = 1, and C = 10, in order from top to bottom (Note that the result is independent of redshift in the case of no recombinations). When recombinations are included, the volume rises and reaches close to V_max before dropping after the source turns off. At large t recombinations stop due to the dropping density, and the volume approaches a constant value (although V << V_max at large t if C = 10).

Figure 46. Expanding H II region around an isolated ionizing source. The comoving ionized volume V is expressed in units of the maximum possible volume, Vmax = 4 rmax3 / 3 [with rmax given in equation (129)], and the time is measured after an instantaneous starburst which produces ionizing photons according to equation (130). We consider a source turning on at z = 10 (solid curves) or z = 15 (dashed curves), with three cases for each: no recombinations, C = 1, and C = 10, in order from top to bottom. The no-recombination curve is identical for the different source redshifts.

We obtain a similar result for the size of the H II region around a galaxy if we consider a mini-quasar rather than stars. For the typical quasar spectrum (Elvis et al. 1994 [122]), roughly 11,000 ionizing photons are produced per baryon incorporated into the black hole, assuming a radiative efficiency of ~ 6%. The efficiency of incorporating the baryons in a galaxy into a central black hole is low (< 0.6% in the local Universe, e.g. Magorrian et al. 1998 [243]), but the escape fraction for quasars is likely to be close to unity, i.e., an order of magnitude higher than for stars (see previous sub-section). Thus, for every baryon in galaxies, up to ~ 65 ionizing photons may be produced by a central black hole and ~ 40 by stars, although both of these numbers for N_ion are highly uncertain. These numbers suggest that in either case the typical size of H II regions before reionization may be < 1 Mpc or ~ 10 Mpc, depending on whether 10⁸ M halos or 10¹² M halos dominate.

The ionization front around a bright transient source like a quasar expands at early times at nearly the speed of light. This occurs when the HII region is sufficiently small so that the production rate of ionizing photons by the central source exceeds their consumption rate by hydrogen atoms within this volume. It is straightforward to do the accounting for these rates (including recombinations) taking the light propagation delay into account. This was done by Wyithe & Loeb [396] [see also White et al. (2003) [381]] who derived the general equation for the relativistic expansion of the comoving radius [r = (1 + z)r_p] of the quasar H II region in an IGM with a neutral filling fraction x_HI (fixed by other ionizing sources) as,

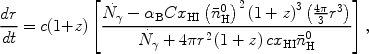(131)

where c is the speed of light, C is the clumping factor, _b = 2.6 × 10^-13 cm³ s^-1 is the case-B recombination coefficient at the characteristic temperature of 10⁴ K, and 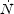is the rate of ionizing photons crossing a shell at the radius of the HII region at time t. Indeed, for 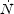the propagation speed of the proper radius of the HII region r_p = r / (1 + z) approaches the speed of light in the above expression, (dr_p / dt) c. The actual size of the HII region along the line-of-sight to a quasar can be inferred from the extent of the spectral gap between the quasar's rest-frame Ly wavelength and the start of Ly absorption by the IGM in the observed spectrum. Existing data from the SDSS quasars [396, 251, 401] provide typical values of r_p ~ 5 Mpc and indicate for plausible choices of the quasar lifetimes that x_HI > 0.1 at z > 6. These ionized bubbles could be imaged directly by future 21cm maps of the regions around the highest-redshift quasars [367, 397, 390].

The profile of the Ly emission line of galaxies has also been suggested as a probe of the ionization state of the IGM [223, 314, 81, 177, 240, 227, 246]. If the IGM is neutral, then the damping wing of the Gunn-Peterson trough in equation (108) is modified since Ly absorption starts only from the near edge of the ionized region along the line-of-sight to the source [81, 240]. Rhoads & Malhotra [246] showed that the observed abundance of galaxies with Ly emission at z ~ 6.5 indicates that a substantial fraction (tens of percent) of the IGM must be ionized in order to allow transmission of the observed Ly photons. However, if these galaxies reside in groups, then galaxies with peculiar velocities away from the observer will preferentially Doppler-shift the emitted Ly photons to the red wing of the Ly resonance and reduce the depression of the line profile [227, 85]. Additional uncertainties in the intrinsic line profile based on the geometry and the stellar or gaseous contents of the source galaxy [227, 314], as well as the clustering of galaxies which ionize their immediate environment in groups [400, 145], limits this method from reaching robust conclusions. Imaging of the expected halos of scattered Ly radiation around galaxies embedded in a neutral IGM [223, 307] provide a more definitive test of the neutrality of the IGM, but is more challenging observationally.

7.3. Reionization of Hydrogen

In this section we summarize recent progress, both analytic and numerical, made toward elucidating the basic physics of reionization and the way in which the characteristics of reionization depend on the nature of the ionizing sources and on other input parameters of cosmological models.

The process of the reionization of hydrogen involves several distinct stages. The initial, "pre-overlap" stage (using the terminology of Gnedin [152]) consists of individual ionizing sources turning on and ionizing their surroundings. The first galaxies form in the most massive halos at high redshift, and these halos are biased and are preferentially located in the highest-density regions. Thus the ionizing photons which escape from the galaxy itself (see Section 7.1) must then make their way through the surrounding high-density regions, which are characterized by a high recombination rate. Once they emerge, the ionization fronts propagate more easily into the low-density voids, leaving behind pockets of neutral, high-density gas. During this period the IGM is a two-phase medium characterized by highly ionized regions separated from neutral regions by ionization fronts. Furthermore, the ionizing intensity is very inhomogeneous even within the ionized regions, with the intensity determined by the distance from the nearest source and by the ionizing luminosity of this source.

The central, relatively rapid "overlap" phase of reionization begins when neighboring H II regions begin to overlap. Whenever two ionized bubbles are joined, each point inside their common boundary becomes exposed to ionizing photons from both sources. Therefore, the ionizing intensity inside H II regions rises rapidly, allowing those regions to expand into high-density gas which had previously recombined fast enough to remain neutral when the ionizing intensity had been low. Since each bubble coalescence accelerates the process of reionization, the overlap phase has the character of a phase transition and is expected to occur rapidly, over less than a Hubble time at the overlap redshift. By the end of this stage most regions in the IGM are able to see several unobscured sources, and therefore the ionizing intensity is much higher than before overlap and it is also much more homogeneous. An additional ingredient in the rapid overlap phase results from the fact that hierarchical structure formation models predict a galaxy formation rate that rises rapidly with time at the relevant redshift range. This process leads to a state in which the low-density IGM has been highly ionized and ionizing radiation reaches everywhere except for gas located inside self-shielded, high-density clouds. This marks the end of the overlap phase, and this important landmark is most often referred to as the 'moment of reionization'.

Some neutral gas does, however, remain in high-density structures which correspond to Lyman Limit systems and damped Ly systems seen in absorption at lower redshifts. The high-density regions are gradually ionized as galaxy formation proceeds, and the mean ionizing intensity also grows with time. The ionizing intensity continues to grow and to become more uniform as an increasing number of ionizing sources is visible to every point in the IGM. This "post-overlap" phase continues indefinitely, since collapsed objects retain neutral gas even in the present Universe. The IGM does, however, reach another milestone at z ~ 1.6, the breakthrough redshift [239]. Below this redshift, all ionizing sources are visible to each other, while above this redshift absorption by the Ly forest implies that only sources in a small redshift range are visible to a typical point in the IGM.

Semi-analytic models of the pre-overlap stage focus on the evolution of the H II filling factor, i.e., the fraction of the volume of the Universe which is filled by H II regions. We distinguish between the naive filling factor F_{H II} and the actual filling factor or porosity Q_{H II}. The naive filling factor equals the number density of bubbles times the average volume of each, and it may exceed unity since when bubbles begin to overlap the overlapping volume is counted multiple times. However, as explained below, in the case of reionization the linearity of the physics means that F_{H II} is a very good approximation to Q_{H II} up to the end of the overlap phase of reionization.

The model of individual H II regions presented in the previous section can be used to understand the development of the total filling factor. Starting with equation (120), if we assume a common clumping factor C for all H II regions then we can sum each term of the equation over all bubbles in a given large volume of the Universe, and then divide by this volume. Then V is replaced by the filling factor and N by the total number of ionizing photons produced up to some time t, per unit volume. The latter quantity equals the mean number of ionizing photons per baryon times the mean density of baryons n_b. Following the arguments leading to equation (129), we find that if we include only stars then

(132)

where the collapse fraction F_col is the fraction of all the baryons in the Universe which are in galaxies, i.e., the fraction of gas which settles into halos and cools efficiently inside them. In writing equation (132) we are assuming instantaneous production of photons, i.e., that the timescale for the formation and evolution of the massive stars in a galaxy is short compared to the Hubble time at the formation redshift of the galaxy. In a model based on equation (120), the near-equality between F_{H II} and Q_{H II} results from the linearity of this equation. First, the total number of ionizations equals the total number of ionizing photons produced by stars, i.e., all ionizing photons contribute regardless of the spatial distribution of sources; and second, the total recombination rate is proportional to the total ionized volume, regardless of its topology. Thus, even if two or more bubbles overlap the model remains an accurate approximation for Q_{H II} (at least until Q_{H II} becomes nearly equal to 1). Note, however, that there still are a number of important simplifications in the model, including the assumption of a homogeneous (though possibly time-dependent) clumping factor, and the neglect of feedback whereby the formation of one galaxy may suppress further galaxy formation in neighboring regions. These complications are discussed in detail below and in Section 7.5 and Section 8.

Under these assumptions we convert equation (120), which describes individual H II regions, to an equation which statistically describes the transition from a neutral Universe to a fully ionized one (compare to Madau et al. 1999 [239] and Haiman & Loeb 1997 [171]):

(133)

where we assumed a primordial mass fraction of hydrogen of 0.76. The solution (in analogy with equation (122)) is

(134)

where F(t', t) is determined by equations (123) - (127).

A simple estimate of the collapse fraction at high redshift is the mass fraction (given by equation (91) in the Press-Schechter model) in halos above the cooling threshold, which is the minimum mass of halos in which gas can cool efficiently. Assuming that only atomic cooling is effective during the redshift range of reionization, the minimum mass corresponds roughly to a halo of virial temperature T_vir = 10⁴ K, which can be converted to a mass using equation (86). With this prescription we derive (for N_ion = 40) the reionization history shown in Fig. 47 for the case of a constant clumping factor C. The solid curves show Q_{H II} as a function of redshift for a clumping factor C = 0 (no recombinations), C = 1, C = 10, and C = 30, in order from left to right. Note that if C ~ 1 then recombinations are unimportant, but if C > 10 then recombinations significantly delay the reionization redshift (for a fixed star-formation history). The dashed curve shows the collapse fraction F_col in this model. For comparison, the vertical dotted line shows the z = 5.8 observational lower limit (Fan et al. 2000 [124]) on the reionization redshift.

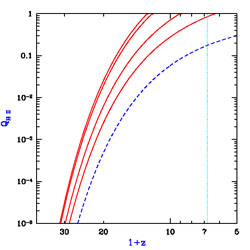Figure 47. Semi-analytic calculation of the reionization of the IGM (for Nion = 40), showing the redshift evolution of the filling factor QH II. Solid curves show QH II for a clumping factor C = 0 (no recombinations), C = 1, C = 10, and C = 30, in order from left to right. The dashed curve shows the collapse fraction Fcol, and the vertical dotted line shows the z = 5.8 observational lower limit (Fan et al. 2000 [124]) on the reionization redshift.

Clearly, star-forming galaxies in CDM hierarchical models are capable of ionizing the Universe at z ~ 6 - 15 with reasonable parameter choices. This has been shown by a large number of theoretical, semi-analytic calculations [138, 330, 171, 373, 89, 92, 392, 83, 371] as well as numerical simulations [79, 148, 152, 2, 296, 95, 342, 204, 186]. Similarly, if a small fraction (< 1%) of the gas in each galaxy accretes onto a central black hole, then the resulting mini-quasars are also able to reionize the Universe, as has also been shown using semi-analytic models [138, 172, 373, 392].

Although many models yield a reionization redshift around 7 - 12, the exact value depends on a number of uncertain parameters affecting both the source term and the recombination term in equation (133). The source parameters include the formation efficiency of stars and quasars and the escape fraction of ionizing photons produced by these sources. The formation efficiency of low mass galaxies may also be reduced by feedback from galactic outflows. These parameters affecting the sources are discussed elsewhere in this review (see Section 7.1, and 8). Even when the clumping is inhomogeneous, the recombination term in equation (133) is generally valid if C is defined as in equation (119), where we take a global volume average of the square of the density inside ionized regions (since neutral regions do not contribute to the recombination rate). The resulting mean clumping factor depends on the density and clustering of sources, and on the distribution and topology of density fluctuations in the IGM. Furthermore, the source halos should tend to form in overdense regions, and the clumping factor is affected by this cross-correlation between the sources and the IGM density.

Miralda-Escudé, Haehnelt, & Rees (2000) [256] presented a simple model for the distribution of density fluctuations, and more generally they discussed the implications of inhomogeneous clumping during reionization. They noted that as ionized regions grow, they more easily extend into low-density regions, and they tend to leave behind high-density concentrations, with these neutral islands being ionized only at a later stage. They therefore argued that, since at high-redshift the collapse fraction is low, most of the high-density regions, which would dominate the clumping factor if they were ionized, will in fact remain neutral and occupy only a tiny fraction of the total volume. Thus, the development of reionization through the end of the overlap phase should occur almost exclusively in the low-density IGM, and the effective clumping factor during this time should be ~ 1, making recombinations relatively unimportant (see Fig. 47). Only in the post-reionization phase, Miralda-Escudé et al. (2000) [256] argued, do the high density clouds and filaments become gradually ionized as the mean ionizing intensity further increases.

The complexity of the process of reionization is illustrated by the numerical simulation of Gnedin [152] of stellar reionization (in CDM with _m = 0.3). This simulation uses a formulation of radiative transfer which relies on several rough approximations; although it does not include the effect of shadowing behind optically-thick clumps, it does include for each point in the IGM the effects of an estimated local optical depth around that point, plus a local optical depth around each ionizing source. This simulation helps to understand the advantages of the various theoretical approaches, while pointing to the complications which are not included in the simple models. Figures 48 and 49, taken from Figure 3 in [152], show the state of the simulated Universe just before and just after the overlap phase, respectively. They show a thin (15 h^-1 comoving kpc) slice through the box, which is 4 h^-1 Mpc on a side, achieves a spatial resolution of 1 h^-1 kpc, and uses 128³ each of dark matter particles and baryonic particles (with each baryonic particle having a mass of 5 × 10⁵ M). The figures show the redshift evolution of the mean ionizing intensity J₂₁ (upper right panel), and visually the logarithm of the neutral hydrogen fraction (upper left panel), the gas density (lower left panel), and the gas temperature (lower right panel). Note the obvious features resulting from the periodic boundary conditions assumed in the simulation. Also note that the intensity J₂₁ is defined as the intensity at the Lyman limit, expressed in units of 10^-21 erg cm^-2 s^-1 sr ^-1Hz^-1. For a given source emission, the intensity inside H II regions depends on absorption and radiative transfer through the IGM (e.g., Haardt & Madau 1996 [166]; Abel & Haehnelt 1999 [1])

Figure 48. Visualization at z = 7.7 of a numerical simulation of reionization, adopted from Figure 3c of [152]. The panels display the logarithm of the neutral hydrogen fraction (upper left), the gas density (lower left), and the gas temperature (lower right). Also shown is the redshift evolution of the logarithm of the mean ionizing intensity (upper right). Note the periodic boundary conditions.

Figure 49. Visualization at z = 6.7 of a numerical simulation of reionization, adopted from Figure 3e of [152]. The panels display the logarithm of the neutral hydrogen fraction (upper left), the gas density (lower left), and the gas temperature (lower right). Also shown is the redshift evolution of the logarithm of the mean ionizing intensity (upper right). Note the periodic boundary conditions.

Figure 48 shows the two-phase IGM at z = 7.7, with ionized bubbles emanating from one main concentration of sources (located at the right edge of the image, vertically near the center; note the periodic boundary conditions). The bubbles are shown expanding into low density regions and beginning to overlap at the center of the image. The topology of ionized regions is clearly complex: While the ionized regions are analogous to islands in an ocean of neutral hydrogen, the islands themselves contain small lakes of dense neutral gas. One aspect which has not been included in theoretical models of clumping is clear from the figure. The sources themselves are located in the highest density regions (these being the sites where the earliest galaxies form) and must therefore ionize the gas in their immediate vicinity before the radiation can escape into the low density IGM. For this reason, the effective clumping factor is of order 100 in the simulation and also, by the overlap redshift, roughly ten ionizing photons have been produced per baryon. Figure 49 shows that by z = 6.7 the low density regions have all become highly ionized along with a rapid increase in the ionizing intensity. The only neutral islands left are the highest density regions (compare the two panels on the left). However, we emphasize that the quantitative results of this simulation must be considered preliminary, since the effects of increased resolution and a more accurate treatment of radiative transfer are yet to be explored. Methods are being developed for incorporating a more complete treatment of radiative transfer into three dimensional cosmological simulations (e.g., [2, 296, 95, 342, 204, 186]).

Gnedin, Ferrara, & Zweibel (2000) [151] investigated an additional effect of reionization. They showed that the Biermann battery in cosmological ionization fronts inevitably generates coherent magnetic fields of an amplitude ~ 10^-19 Gauss. These fields form as a result of the breakout of the ionization fronts from galaxies and their propagation through the H I filaments in the IGM. Although the fields are too small to directly affect galaxy formation, they could be the seeds for the magnetic fields observed in galaxies and X-ray clusters today.

If quasars contribute substantially to the ionizing intensity during reionization then several aspects of reionization are modified compared to the case of pure stellar reionization. First, the ionizing radiation emanates from a single, bright point-source inside each host galaxy, and can establish an escape route (H II funnel) more easily than in the case of stars which are smoothly distributed throughout the galaxy (Section 7.1). Second, the hard photons produced by a quasar penetrate deeper into the surrounding neutral gas, yielding a thicker ionization front. Finally, the quasar X-rays catalyze the formation of H₂ molecules and allow stars to keep forming in very small halos.

Oh (1999) [270] showed that star-forming regions may also produce significant X-rays at high redshift. The emission is due to inverse Compton scattering of CMB photons off relativistic electrons in the ejecta, as well as thermal emission by the hot supernova remnant. The spectrum expected from this process is even harder than for typical quasars, and the hard photons photoionize the IGM efficiently by repeated secondary ionizations. The radiation, characterized by roughly equal energy per logarithmic frequency interval, would produce a uniform ionizing intensity and lead to gradual ionization and heating of the entire IGM. Thus, if this source of emission is indeed effective at high redshift, it may have a crucial impact in changing the topology of reionization. Even if stars dominate the emission, the hardness of the ionizing spectrum depends on the initial mass function. At high redshift it may be biased toward massive, efficiently ionizing stars, but this remains very much uncertain.

Semi-analytic as well as numerical models of reionization depend on an extrapolation of hierarchical models to higher redshifts and lower-mass halos than the regime where the models have been compared to observations (see e.g. [392, 83, 371]). These models have the advantage that they are based on the current CDM paradigm which is supported by a variety of observations of large-scale structure, galaxy clustering, and the CMB. The disadvantage is that the properties of high-redshift galaxies are derived from those of their host halos by prescriptions which are based on low redshift observations, and these prescriptions will only be tested once abundant data is available on galaxies which formed during the reionization era (see [392] for the sensitivity of the results to model parameters). An alternative approach to analyzing the possible ionizing sources which brought about reionization is to extrapolate from the observed populations of galaxies and quasars at currently accessible redshifts. This has been attempted, e.g., by Madau et al. (1999) [239] and Miralda-Escudé et al. (2000) [256]. The general conclusion is that a high-redshift source population similar to the one observed at z = 3 - 4 would produce roughly the needed ionizing intensity for reionization. However, Dijkstra, Haiman, & Loeb (2004) [107] constrained the role of quasars in reionizing the Universe based on the unresolved flux of the X-ray background. At any event, a precise conclusion remains elusive because of the same kinds of uncertainties as those found in the models based on CDM: The typical escape fraction, and the faint end of the luminosity function, are both not well determined even at z = 3 - 4, and in addition the clumping factor at high redshift must be known in order to determine the importance of recombinations. Future direct observations of the source population at redshifts approaching reionization may help resolve some of these questions.

7.4. Photo-evaporation of Gaseous Halos After Reionization

The end of the reionization phase transition resulted in the emergence of an intense UV background that filled the Universe and heated the IGM to temperatures of ~ 1 - 2 × 10⁴ K (see the previous section). After ionizing the rarefied IGM in the voids and filaments on large scales, the cosmic UV background penetrated the denser regions associated with the virialized gaseous halos of the first generation of objects. A major fraction of the collapsed gas had been incorporated by that time into halos with a virial temperature < 10⁴ K, where the lack of atomic cooling prevented the formation of galactic disks and stars or quasars. Photoionization heating by the cosmic UV background could then evaporate much of this gas back into the IGM. The photo-evaporating halos, as well as those halos which did retain their gas, may have had a number of important consequences just after reionization as well as at lower redshifts.

In this section we focus on the process by which gas that had already settled into virialized halos by the time of reionization was evaporated back into the IGM due to the cosmic UV background. This process was investigated by Barkana & Loeb (1999) [22] using semi-analytic methods and idealized numerical calculations. They first considered an isolated spherical, centrally-concentrated dark matter halo containing gas. Since most of the photo-evaporation occurs at the end of overlap, when the ionizing intensity builds up almost instantaneously, a sudden illumination by an external ionizing background may be assumed. Self-shielding of the gas implies that the halo interior sees a reduced intensity and a harder spectrum, since the outer gas layers preferentially block photons with energies just above the Lyman limit. It is useful to parameterize the external radiation field by a specific intensity per unit frequency, ,

(135)

where _L is the Lyman limit frequency, and J₂₁ is the intensity at _L expressed in units of 10^-21 erg cm^-2 s^-1 sr ^-1Hz^-1. The intensity is normalized to an expected post - reionization value of around unity for the ratio of ionizing photon density to the baryon density. Different power laws can be used to represent either quasar spectra ( ~ 1.8) or stellar spectra ( ~ 5).

Once the gas is heated throughout the halo, some fraction of it acquires a sufficiently high temperature that it becomes unbound. This gas expands due to the resulting pressure gradient and eventually evaporates back into the IGM. The pressure gradient force (per unit volume) k (T / µm_p) competes with the gravitational force of G M / r². Due to the density gradient, the ratio between the pressure force and the gravitational force is roughly equal to the ratio between the thermal energy ~ k T and the gravitational binding energy ~ µm_p G M / r (which is ~ k T_vir at the virial radius r_vir) per particle. Thus, if the kinetic energy exceeds the potential energy (or roughly if T> T_vir), the repulsive pressure gradient force exceeds the attractive gravitational force and expels the gas on a dynamical time (or faster for halos with T >> T_vir).

The left panel of Figure 50 (adopted from Fig. 3 of Barkana & Loeb 1999 [22]) shows the fraction of gas within the virial radius which becomes unbound after reionization, as a function of the total halo circular velocity, with halo masses at z = 8 indicated at the top. The two pairs of curves correspond to spectral index = 5 (solid) or = 1.8 (dashed). In each pair, a calculation which assumes an optically-thin halo leads to the upper curve, but including radiative transfer and self-shielding modifies the result to the one shown by the lower curve. In each case self-shielding lowers the unbound fraction, but it mostly affects only a neutral core containing ~ 30% of the gas. Since high energy photons above the Lyman limit penetrate deep into the halo and heat the gas efficiently, a flattening of the spectral slope from = 5 to = 1.8 raises the unbound gas fraction. This figure is essentially independent of redshift if plotted in terms of circular velocity, but the conversion to a corresponding mass does vary with redshift. The characteristic circular velocity where most of the gas is lost is ~ 10 - 15 km s^-1, but clearly the effect of photo-evaporation is gradual, going from total gas removal down to no effect over a range of a factor of ~ 100 in halo mass.

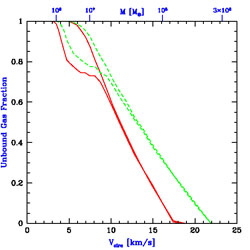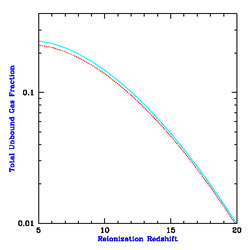Figure 50. Effect of photo-evaporation on individual halos and on the overall halo population. The left panel shows the unbound gas fraction (within the virial radius) versus total halo velocity dispersion or mass, adopted from Figure 3 of Barkana & Loeb (1999) [22]. The two pairs of curves correspond to spectral index = 5 (solid) or = 1.8 (dashed), in each case at z = 8. In each pair, assuming an optically-thin halo leads to the upper curve, while the lower curve shows the result of including radiative transfer and self shielding. The right panel shows the total fraction of gas in the Universe which evaporates from halos at reionization, versus the reionization redshift, adopted from Figure 7 of Barkana & Loeb (1999) [22]. The solid line assumes a spectral index = 1.8, and the dotted line assumes = 5.

Given the values of the unbound gas fraction in halos of different masses, the Press-Schechter mass function (Section 4.1) can be used to calculate the total fraction of the IGM which goes through the process of accreting onto a halo and then being recycled into the IGM at reionization. The low-mass cutoff in this sum over halos is given by the lowest mass halo in which gas has assembled by the reionization redshift. This mass can be estimated by the linear Jeans mass M_J in equation (62). The Jeans mass does not in general precisely equal the limiting mass for accretion (see the discussion in the next section). Indeed, at a given redshift some gas can continue to fall into halos of lower mass than the Jeans mass at that redshift. On the other hand, the larger Jeans mass at higher redshifts means that a time-averaged Jeans mass may be more appropriate, as indicated by the filtering mass. In practice, the Jeans mass is sufficiently accurate since at z ~ 10 - 20 it agrees well with the values found in the numerical spherical collapse calculations of Haiman, Thoul, & Loeb (1996) [168].

The right panel of Figure 50 (adopted from Fig. 7 of Barkana & Loeb 1999 [22]) shows the total fraction of gas in the Universe which evaporates from halos at reionization, versus the reionization redshift. The solid line assumes a spectral index = 1.8, and the dotted line assumes = 5, showing that the result is insensitive to the spectrum. Even at high redshift, the amount of gas which participates in photo-evaporation is significant, which suggests a number of possible implications as discussed below. The gas fraction shown in the figure represents most (~ 60 - 80% depending on the redshift) of the collapsed fraction before reionization, although some gas does remain in more massive halos.

The photo-evaporation of gas out of large numbers of halos may have interesting implications. First, gas which falls into halos and is expelled at reionization attains a different entropy than if it had stayed in the low-density IGM. The resulting overall reduction in the entropy is expected to be small - the same as would be produced by reducing the temperature of the entire IGM by a factor of ~ 1.5 - but localized effects near photo-evaporating halos may be more significant. Furthermore, the resulting ~ 20 km s^-1 outflows induce small-scale fluctuations in peculiar velocity and temperature. These outflows are usually well below the resolution limit of most numerical simulations, but some outflows were resolved in the simulation of Bryan et al. (1998) [70]. The evaporating halos may consume a significant number of ionizing photons in the post-overlap stage of reionization [174, 186], but a definitive determination requires detailed simulations which include the three-dimensional geometry of source halos and sink halos.

Although gas is quickly expelled out of the smallest halos, photo-evaporation occurs more gradually in larger halos which retain some of their gas. These surviving halos initially expand but they continue to accrete dark matter and to merge with other halos. These evaporating gas halos could contribute to the high column density end of the Ly forest [51]. Abel & Mo (1998) [3] suggested that, based on the expected number of surviving halos, a large fraction of the Lyman limit systems at z ~ 3 may correspond to mini-halos that survived reionization. Surviving halos may even have identifiable remnants in the present Universe. These ideas thus offer the possibility that a population of halos which originally formed prior to reionization may correspond almost directly to several populations that are observed much later in the history of the Universe. However, the detailed dynamics of photo-evaporating halos are complex, and detailed simulations are required to confirm these ideas. Photo-evaporation of a gas cloud has been followed in a two dimensional simulation with radiative transfer, by Shapiro & Raga (2000) [331]. They found that an evaporating halo would indeed appear in absorption as a damped Ly system initially, and as a weaker absorption system subsequently. Future simulations [186] will clarify the contribution to quasar absorption lines of the entire population of photo-evaporating halos.

7.5. Suppression of the Formation of Low Mass Galaxies

At the end of overlap, the cosmic ionizing background increased sharply, and the IGM was heated by the ionizing radiation to a temperature > 10⁴ K. Due to the substantial increase in the IGM temperature, the intergalactic Jeans mass increased dramatically, changing the minimum mass of forming galaxies [299, 117, 148, 255].

Gas infall depends sensitively on the Jeans mass. When a halo more massive than the Jeans mass begins to form, the gravity of its dark matter overcomes the gas pressure. Even in halos below the Jeans mass, although the gas is initially held up by pressure, once the dark matter collapses its increased gravity pulls in some gas [168]. Thus, the Jeans mass is generally higher than the actual limiting mass for accretion. Before reionization, the IGM is cold and neutral, and the Jeans mass plays a secondary role in limiting galaxy formation compared to cooling. After reionization, the Jeans mass is increased by several orders of magnitude due to the photoionization heating of the IGM, and hence begins to play a dominant role in limiting the formation of stars. Gas infall in a reionized and heated Universe has been investigated in a number of numerical simulations. Thoul & Weinberg (1996) [363] inferred, based on a spherically-symmetric collapse simulation, a reduction of ~ 50% in the collapsed gas mass due to heating, for a halo of circular velocity V_c ~ 50 km s^-1 at z = 2, and a complete suppression of infall below V_c ~ 30 km s^-1. Kitayama & Ikeuchi (2000) [201] also performed spherically-symmetric simulations but included self-shielding of the gas, and found that it lowers the circular velocity thresholds by ~ 5 km s^-1. Three dimensional numerical simulations [294, 378, 267] found a significant suppression of gas infall in even larger halos (V_c ~ 75 km s^-1), but this was mostly due to a suppression of late infall at z < 2.

When a volume of the IGM is ionized by stars, the gas is heated to a temperature T_IGM ~ 10⁴ K. If quasars dominate the UV background at reionization, their harder photon spectrum leads to T_IGM > 2 × 10⁴ K. Including the effects of dark matter, a given temperature results in a linear Jeans mass corresponding to a halo circular velocity of

(136)

where we used equation (85) and assumed µ = 0.6. In halos with V_c > V_J, the gas fraction in infalling gas equals the universal mean of _b / _m, but gas infall is suppressed in smaller halos. Even for a small dark matter halo, once it collapses to a virial overdensity of _c / _m ^z relative to the mean, it can pull in additional gas. A simple estimate of the limiting circular velocity, below which halos have essentially no gas infall, is obtained by substituting the virial overdensity for the mean density in the definition of the Jeans mass. The resulting estimate is

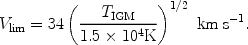(137)

This value is in rough agreement with the numerical simulations mentioned before. A more recent study by Dijkstra et al. (2004) [107] indicates that at the high redshifts of z > 10 gas could nevertheless assemble into halos with circular velocities as low as v_c ~ 10 km s^-1, even in the presence of a UV background.

Although the Jeans mass is closely related to the rate of gas infall at a given time, it does not directly yield the total gas residing in halos at a given time. The latter quantity depends on the entire history of gas accretion onto halos, as well as on the merger histories of halos, and an accurate description must involve a time-averaged Jeans mass. Gnedin [153] showed that the gas content of halos in simulations is well fit by an expression which depends on the filtering mass, a particular time-averaged Jeans mass (Gnedin & Hui 1998 [150]). Gnedin [153] calculated the Jeans and filtering masses using the mean temperature in the simulation to define the sound speed, and found the following fit to the simulation results:

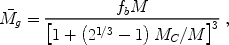(138)

where _g is the average gas mass of all objects with a total mass M, f_b = _b / _m is the universal baryon fraction, and the characteristic mass M_c is the total mass of objects which on average retain 50% of their gas mass. The characteristic mass was well fit by the filtering mass at a range of redshifts from z = 4 up to z ~ 15.

The reionization process was not perfectly synchronized throughout the Universe. Large-scale regions with a higher density than the mean tend to form galaxies first and reionize earlier than underdense regions (see detailed discussion in Section 9.2). The suppression of low-mass galaxies by reionization will therefore be modulated by the fluctuations in the timing of reionization. Babich & Loeb (2005) [14] considered the effect of inhomogeneous reionization on the power-spectrum of low-mass galaxies. They showed that the shape of the high redshift galaxy power spectrum on small scales in a manner which depends on the details of epoch of reionization. This effect is significantly larger than changes in the galaxy power spectrum due to the current uncertainty in the inflationary parameters, such as the tilt of the scalar power spectrum n and the running of the tilt . Therefore, future high redshift galaxies surveys hoping to constrain inflationary parameters must properly model the effects of reionization, but conversely they will also be sensitive to the thermal history of the high redshift intergalactic medium.

⁸ The recombination rate depends on the number density of electrons, and in using equation (119) we are neglecting the small contribution caused by partially or fully ionized helium. Back.