8. FEEDBACK FROM GALACTIC OUTFLOWS

8.1. Propagation of Supernova Outflows in the IGM

Star formation is accompanied by the violent death of massive stars in supernova explosions. In general, if each halo has a fixed baryon fraction and a fixed fraction of the baryons turns into massive stars, then the total energy in supernovae outflows is proportional to the halo mass. The binding energy of the gas in the halo is proportional to the halo mass squared. Thus, outflows are expected to escape more easily out of low-mass galaxies, and to expel a greater fraction of the gas from dwarf galaxies. At high redshifts, most galaxies form in relatively low-mass halos, and the high halo merger rate leads to vigorous star formation. Thus, outflows may have had a great impact on the earliest generations of galaxies, with consequences that may include metal enrichment of the IGM and the disruption of dwarf galaxies. In this subsection we present a simple model for the propagation of individual supernova shock fronts in the IGM. We discuss some implications of this model, but we defer to the following subsection the brunt of the discussion of the cosmological consequences of outflows.

For a galaxy forming in a given halo, the supernova rate is related to the star formation rate. In particular, for a Scalo (1998) [315] initial stellar mass function, if we assume that a supernova is produced by each M > 8 M star, then on average one supernova explodes for every 126 M of star formation, expelling an ejecta mass of ~ 3 M including ~ 1 M of heavy elements. We assume that the individual supernovae produce expanding hot bubbles which merge into a single overall region delineated by an outwardly moving shock front. We assume that most of the baryons in the outflow lie in a thin shell, while most of the thermal energy is carried by the hot interior. The total ejected mass equals a fraction f_gas of the total halo gas which is lifted out of the halo by the outflow. This gas mass includes a fraction f_eject of the mass of the supernova ejecta itself (with f_eject 1 since some metals may be deposited in the disk and not ejected). Since at high redshift most of the halo gas is likely to have cooled onto a disk, we assume that the mass carried by the outflow remains constant until the shock front reaches the halo virial radius. We assume an average supernova energy of 10⁵¹ E₅₁ erg, a fraction f_wind of which remains in the outflow after it escapes from the disk. The outflow must overcome the gravitational potential of the halo, which we assume to have a Navarro, Frenk, & White (1997) [266] density profile [NFW; see equation (88)]. Since the entire shell mass must be lifted out of the halo, we include the total shell mass as well as the total injected energy at the outset. This assumption is consistent with the fact that the burst of star formation in a halo is typically short compared to the total time for which the corresponding outflow expands.

The escape of an outflow from an NFW halo depends on the concentration parameter c_N of the halo. Simulations by Bullock et al. (2000) [72] indicate that the concentration parameter decreases with redshift, and their results may be extrapolated to our regime of interest (i.e., to smaller halo masses and higher redshifts) by assuming that

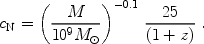(139)

Although we calculate below the dynamics of each outflow in detail, it is also useful to estimate which halos can generate large-scale outflows by comparing the kinetic energy of the outflow to the potential energy needed to completely escape (i.e., to infinite distance) from an NFW halo. We thus find that the outflow can escape from its originating halo if the circular velocity is below a critical value given by

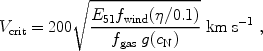(140)

where the efficiency is the fraction of baryons incorporated in stars, and

(141)

Note that the contribution to f_gas of the supernova ejecta itself is 0.024 f_eject, so the ejecta mass is usually negligible unless f_gas < 1%. Equation (140) can also be used to yield the maximum gas fraction f_gas which can be ejected from halos, as a function of their circular velocity. Although this equation is most general, if we assume that the parameters f_gas and f_wind are independent of M and z then we can normalize them based on low-redshift observations. If we specify c_N ~ 10 (with g(10) = 6.1) at z = 0, then setting E₅₁ = 1 and = 10% yields the required energy efficiency as a function of the ejected halo gas fraction:

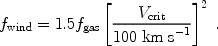(142)

A value of V_crit ~ 100 km s^-1 is suggested by several theoretical and observational arguments which are discussed in the next subsection. However, these arguments are not conclusive, and V_crit may differ from this value by a large factor, especially at high redshift (where outflows are observationally unconstrained at present). Note the degeneracy between f_gas and f_wind which remains even if V_crit is specified. Thus, if V_crit ~ 100 km s^-1 then a high efficiency f_wind ~ 1 is required to eject most of the gas from all halos with V_c < V_crit, but only f_wind ~ 10% is required to eject 5 - 10% of the gas. The evolution of the outflow does depend on the value of f_wind and not just the ratio f_wind / f_gas, since the shell accumulates material from the IGM which eventually dominates over the initial mass carried by the outflow.

We solve numerically for the spherical expansion of a galactic outflow, elaborating on the basic approach of Tegmark, Silk, & Evrard (1993) [358]. We assume that most of the mass m carried along by the outflow lies in a thin, dense, relatively cool shell of proper radius R. The interior volume, while containing only a fraction f_int << 1 of the mass m, carries most of the thermal energy in a hot, isothermal plasma of pressure p_int and temperature T. We assume a uniform exterior gas, at the mean density of the Universe (at each redshift), which may be neutral or ionized, and may exert a pressure p_ext as indicated below. We also assume that the dark matter distribution follows the NFW profile out to the virial radius, and is at the mean density of the Universe outside the halo virial radius. Note that in reality an overdense distribution of gas as well as dark matter may surround each halo due to secondary infall.

The shell radius R in general evolves as follows:

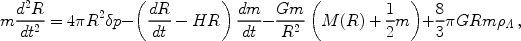(143)

where the right-hand-side includes forces due to pressure, sweeping up of additional mass, gravity, and a cosmological constant, respectively. The shell is accelerated by internal pressure and decelerated by external pressure, i.e., p = p_int - p_ext. In the gravitational force, M(R) is the total enclosed mass, not including matter in the shell, and 1/2m is the effective contribution of the shell mass in the thin-shell approximation [279]. The interior pressure is determined by energy conservation, and evolves according to [358]:

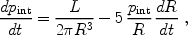(144)

where the luminosity L incorporates heating and cooling terms. We include in L the supernova luminosity L_sn (during a brief initial period of energy injection), cooling terms L_cool, ionization L_ion, and dissipation L_diss. For simplicity, we assume ionization equilibrium for the interior plasma, and a primordial abundance of hydrogen and helium. We include in L_cool all relevant atomic cooling processes in hydrogen and helium, i.e., collisional processes, Bremsstrahlung emission, and Compton cooling off the CMB. Compton scattering is the dominant cooling process for high-redshift outflows. We include in L_ion only the power required to ionize the incoming hydrogen upstream, at the energy cost of 13.6 eV per hydrogen atom. The interaction between the expanding shell and the swept-up mass dissipates kinetic energy. The fraction f_d of this energy which is re-injected into the interior depends on complex processes occurring near the shock front, including turbulence, non-equilibrium ionization and cooling, and so (following Tegmark et al. 1993 [358]) we let

(145)

where we set f_d = 1 and compare below to the other extreme of f_d = 0.

In an expanding Universe, it is preferable to describe the propagation of outflows in terms of comoving coordinates since, e.g., the critical result is the maximum comoving size of each outflow, since this size yields directly the total IGM mass which is displaced by the outflow and injected with metals. Specifically, we apply the following transformation [328, 374]:

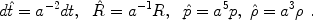(146)

For = 0, Voit (1996) [374] obtained (with the time origin 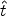= 0 at redshift z₁):

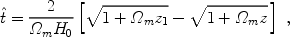(147)

while for _m + = 1 there is no simple analytic expression. We set = / _vir, in terms of the virial radius r_vir [equation (84)] of the source halo. We define _s¹ as the ratio of the shell mass m to 4/3 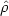_{b vir}³, where 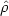_b = _b(z = 0) is the mean baryon density of the Universe at z = 0. More generally, we define

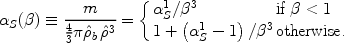(148)

Here we assumed, as noted above, that the shell mass is constant until the halo virial radius is reached, at which point the outflow begins to sweep up material from the IGM. We thus derive the following equations:

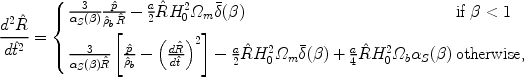(149)

along with

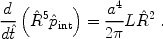(150)

In the evolution equation for , for < 1 we assume for simplicity that the baryons are distributed in the same way as the dark matter, since in any case the dark matter halo dominates the gravitational force. For > 1, however, we correct (via the last term on the right-hand side) for the presence of mass in the shell, since at >> 1 this term may become important. The > 1 equation also includes the braking force due to the swept-up IGM mass. The enclosed mean overdensity for the NFW profile [Eq. (88)] surrounded by matter at the mean density is

(151)

The physics of supernova shells is discussed in Ostriker & McKee (1988) [279] along with a number of analytical solutions. The propagation of cosmological blast waves has also been computed by Ostriker & Cowie (1981) [278], Bertschinger (1985) [40] and Carr & Ikeuchi (1985) [74]. Voit (1996) [374] derived an exact analytic solution to the fluid equations which, although of limited validity, is nonetheless useful for understanding roughly how the outflow size depends on several of the parameters. The solution requires an idealized case of an outflow which at all times expands into a homogeneous IGM. Peculiar gravitational forces, and the energy lost in escaping from the host halo, are neglected, cooling and ionization losses are also assumed to be negligible, and the external pressure is not included. The dissipated energy is assumed to be retained, i.e., f_d is set equal to unity. Under these conditions, the standard Sedov self-similar solution [324, 325] generalizes to the cosmological case as follows [374]:

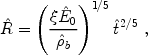(152)

where = 2.026 and 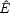₀ = E₀ / (1 + z₁)² in terms of the initial (i.e., at t = 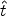= 0 and z = z₁) energy E₀. Numerically, the comoving radius is

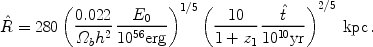(153)

In solving the equations described above, we assume that the shock front expands into a pre-ionized region which then recombines after a time determined by the recombination rate. Thus, the external pressure is included initially, it is turned off after the pre-ionized region recombines, and it is then switched back on at a lower redshift when the Universe is reionized. When the ambient IGM is neutral and the pressure is off, the shock loses energy to ionization. In practice we find that the external pressure is unimportant during the initial expansion, although it is generally important after reionization. Also, at high redshift ionization losses are much smaller than losses due to Compton cooling. In the results shown below, we assume an instantaneous reionization at z = 9.

Figure 51 shows the results for a starting redshift z = 15, for a halo of mass 5.4 × 10⁷ M, stellar mass 8.0 × 10⁵ M, comoving r_vir = 12 kpc, and circular velocity V_c = 20 km/s. We show the shell comoving radius in units of the virial radius of the source halo (top panel), and the physical peculiar velocity of the shock front (bottom panel). Results are shown (solid curve) for the standard set of parameters f_int = 0.1, f_d = 1, f_wind = 75%, and f_gas = 50%. For comparison, we show several cases which adopt the standard parameters except for no cooling (dotted curve), no reionization (short-dashed curve), f_d = 0 (long-dashed curve), or f_wind = 15% and f_gas = 10% (dot-short dashed curve). When reionization is included, the external pressure halts the expanding bubble. We freeze the radius at the point of maximum expansion (where d / d = 0), since in reality the shell will at that point begin to spread and fill out the interior volume due to small-scale velocities in the IGM. For the chosen parameters, the bubble easily escapes from the halo, but when f_wind and f_gas are decreased the accumulated IGM mass slows down the outflow more effectively. In all cases the outflow reaches a size of 10 - 20 times r_vir, i.e., 100 - 200 comoving kpc. If all the metals are ejected (i.e., f_eject = 1), then this translates to an average metallicity in the shell of ~ 1 - 5 × 10^-3 in units of the solar metallicity (which is 2% by mass). The asymptotic size of the outflow varies roughly as f_wind^1/5, as predicted by the simple solution in equation (152), but the asymptotic size is rather insensitive to f_gas (at a fixed f_wind) since the outflow mass becomes dominated by the swept-up IGM mass once > 4_vir. With the standard parameter values (i.e., those corresponding to the solid curve), Figure 51 also shows (dot-long dashed curve) the Voit (1996) [374] solution of equation (152). The Voit solution behaves similarly to the no-reionization curve at low redshift, although it overestimates the shock radius by ~ 30%, and the overestimate is greater compared to the more realistic case which does include reionization.

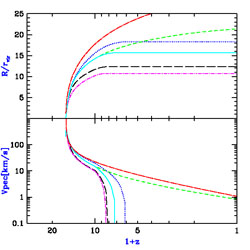Figure 51. Evolution of a supernova outflow from a z = 15 halo of circular velocity Vc = 20 km/s. Plotted are the shell comoving radius in units of the virial radius of the source halo (top panel), and the physical peculiar velocity of the shock front (bottom panel). Results are shown for the standard parameters fint = 0.1, fd = 1, fwind = 75%, and fgas = 50% (solid curve). Also shown for comparison are the cases of no cooling (dotted curve), no reionization (short-dashed curve), fd = 0 (long-dashed curve), or fwind = 15% and fgas = 10% (dot-short dashed curve), as well as the simple Voit (1996) [374] solution of equation (152) for the standard parameter set (dot-long dashed curve). In cases where the outflow halts, we freeze the radius at the point of maximum expansion.

Figure 52 shows different curves than Figure 51 but on an identical layout. A single curve starting at z = 15 (solid curve) is repeated from Figure 51, and it is compared here to outflows with the same parameters but starting at z = 20 (dotted curve), z = 10 (short-dashed curve), and z = 5 (long-dashed curve). A V_c = 20 km/s halo, with a stellar mass equal to 1.5% of the total halo mass, is chosen at the three higher redshifts, but at z = 5 a V_c = 42 km/s halo is assumed. Because of the suppression of gas infall after reionization, we assume that the z = 5 outflow is produced by supernovae from a stellar mass equal to only 0.3% of the total halo mass (with a similarly reduced initial shell mass), thus leading to a relatively small final shell radius. The main conclusion from both figures is the following: In all cases, the outflow undergoes a rapid initial expansion over a fractional redshift interval z / z ~ 0.2, at which point the shell has slowed down to ~ 10 km/s from an initial 300 km/s. The rapid deceleration is due to the accumulating IGM mass. External pressure from the reionized IGM completely halts all high-redshift outflows, and even without this effect most outflows would only move at ~ 10 km/s after the brief initial expansion. Thus, it may be possible for high-redshift outflows to pollute the Lyman alpha forest with metals without affecting the forest hydrodynamically at z < 4. While the bulk velocities of these outflows may dissipate quickly, the outflows do sweep away the IGM and create empty bubbles. The resulting effects on observations of the Lyman alpha forest should be studied in detail (some observational signatures of feedback have been suggested recently by Theuns, Mo, & Schaye 2000 [362]).

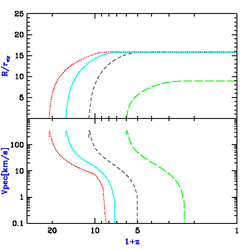Figure 52. Evolution of supernova outflows at different redshifts. The top and bottom panels are arranged similarly to Figure 51. The z = 15 outflow (solid curve) is repeated from Figure 51, and it is compared here to outflows with the same parameters but starting at z = 20 (dotted curve), z = 10 (short-dashed curve), and z = 5 (long-dashed curve). A Vc = 20 km/s halo is assumed except for z = 5, in which case a Vc = 42 km/s halo is assumed to produce the outflow (see text).

Furlanetto & Loeb (2003) [141] derived the evolution of the characteristic scale and filling fraction of supernova-driven bubbles based on a refinement of this formalism (see also their 2001 paper for quasar-driven outflows). The role of metal-rich outflows in smearing the transition epoch between Pop-III (metal-free) and Pop II (metal-enriched) stars, was also analysed by Furlanetto & Loeb (2005) [144], who concluded that a double-reionization history in which the ionization fraction goes through two (or more) peaks is unlikely.

8.2. Effect of Outflows on Dwarf Galaxies and on the IGM

Galactic outflows represent a complex feedback process which affects the evolution of cosmic gas through a variety of phenomena. Outflows inject hydrodynamic energy into the interstellar medium of their host galaxy. As shown in the previous subsection, even a small fraction of this energy suffices to eject most of the gas from a dwarf galaxy, perhaps quenching further star formation after the initial burst. At the same time, the enriched gas in outflows can mix with the interstellar medium and with the surrounding IGM, allowing later generations of stars to form more easily because of metal-enhanced cooling. On the other hand, the expanding shock waves may also strip gas in surrounding galaxies and suppress star formation.

Dekel & Silk (1986) [104] attempted to explain the different properties of diffuse dwarf galaxies in terms of the effect of galactic outflows. They noted the observed trends whereby lower-mass dwarf galaxies have a lower surface brightness and metallicity, but a higher mass-to-light ratio, than higher mass galaxies. They argued that these trends are most naturally explained by substantial gas removal from an underlying dark matter potential. Galaxies lying in small halos can eject their remaining gas after only a tiny fraction of the gas has turned into stars, while larger galaxies require more substantial star formation before the resulting outflows can expel the rest of the gas. Assuming a wind efficiency f_wind ~ 100%, Dekel & Silk showed that outflows in halos below a circular velocity threshold of V_crit ~ 100 km/s have sufficient energy to expel most of the halo gas. Furthermore, cooling is very efficient for the characteristic gas temperatures associated with V_crit < 100 km/s halos, but it becomes less efficient in more massive halos. As a result, this critical velocity is expected to signify a dividing line between bright galaxies and diffuse dwarf galaxies. Although these simple considerations may explain a number of observed trends, many details are still not conclusively determined. For instance, even in galaxies with sufficient energy to expel the gas, it is possible that this energy gets deposited in only a small fraction of the gas, leaving the rest almost unaffected.

Since supernova explosions in an inhomogeneous interstellar medium lead to complicated hydrodynamics, in principle the best way to determine the basic parameters discussed in the previous subsection (f_wind, f_gas, and f_eject) is through detailed numerical simulations of individual galaxies. Mac Low & Ferrara (1999) [235] simulated a gas disk within a z = 0 dark matter halo. The disk was assumed to be azimuthally symmetric and initially smooth. They represented supernovae by a central source of energy and mass, assuming a constant luminosity which is maintained for 50 million years. They found that the hot, metal-enriched ejecta can in general escape from the halo much more easily than the colder gas within the disk, since the hot gas is ejected in a tube perpendicular to the disk without displacing most of the gas in the disk. In particular, most of the metals were expelled except for the case with the most massive halo considered (with 10⁹ M in gas) and the lowest luminosity (10³⁷ erg/s, or a total injection of 2 × 10⁵² erg). On the other hand, only a small fraction of the total gas mass was ejected except for the least massive halo (with 10⁶ M in gas), where a luminosity of 10³⁸ erg/s or more expelled most of the gas. We note that beyond the standard issues of numerical resolution and convergence, there are several difficulties in applying these results to high-redshift dwarf galaxies. Clumping within the expanding shells or the ambient interstellar medium may strongly affect both the cooling and the hydrodynamics. Also, the effect of distributing the star formation throughout the disk is unclear since in that case several characteristics of the problem will change; many small explosions will distribute the same energy over a larger gas volume than a single large explosion [as in the Sedov (1959) [324] solution; see, e.g., equation (152)], and the geometry will be different as each bubble tries to dig its own escape route through the disk. Also, high-redshift disks should be denser by orders of magnitude than z = 0 disks, due to the higher mean density of the Universe at early times. Thus, further numerical simulations of this process are required in order to assess its significance during the reionization epoch.

Some input on these issues also comes from observations. Martin (1999) [247] showed that the hottest extended X-ray emission in galaxies is characterized by a temperature of ~ 10^6.7 K. This hot gas, which is lifted out of the disk at a rate comparable to the rate at which gas goes into new stars, could escape from galaxies with rotation speeds of < 130 km/s. However, these results are based on a small sample which includes only the most vigorous star-forming local galaxies, and the mass-loss rate depends on assumptions about the poorly understood transfer of mass and energy among the various phases of the interstellar medium.

Many authors have attempted to estimate the overall cosmological effects of outflows by combining simple models of individual outflows with the formation rate of galaxies, obtained via semi-analytic methods [98, 358, 374, 265, 129, 317] or numerical simulations [148, 149, 80, 9]. The main goal of these calculations is to explain the characteristic metallicities of different environments as a function of redshift. For example, the IGM is observed to be enriched with metals at redshifts z < 5. Identification of C IV, Si IV an O VI absorption lines which correspond to Ly absorption lines in the spectra of high-redshift quasars has revealed that the low-density IGM has been enriched to a metal abundance (by mass) of Z_IGM ~ 10^{-2.5 ( ± 0.5)} Z, where Z = 0.019 is the solar metallicity [252, 372, 347, 229, 99, 346, 121]. The metal enrichment has been clearly identified down to H I column densities of ~ 10^14.5 cm^-2. The detailed comparison of cosmological hydrodynamic simulations with quasar absorption spectra has established that the forest of Ly absorption lines is caused by the smoothly-fluctuating density of the neutral component of the IGM [84, 405, 180]. The simulations show a strong correlation between the H I column density and the gas overdensity _gas [102], implying that metals were dispersed into regions with an overdensity as low as _gas ~ 3 or possibly even lower.

In general, dwarf galaxies are expected to dominate metal enrichment at high-redshift for several reasons. As noted above and in the previous subsection, outflows can escape more easily out of the potential wells of dwarfs. Also, at high redshift, massive halos are rare and dwarf halos are much more common. Finally, as already noted, the Sedov (1959) [324] solution [or equation (152)] implies that for a given total energy and expansion time, multiple small outflows fill large volumes more effectively than would a smaller number of large outflows. Note, however, that the strong effect of feedback in dwarf galaxies may also quench star formation rapidly and reduce the efficiency of star formation in dwarfs below that found in more massive galaxies.

Cen & Ostriker (1999) [80] showed via numerical simulation that metals produced by supernovae do not mix uniformly over cosmological volumes. Instead, at each epoch the highest density regions have much higher metallicity than the low-density IGM. They noted that early star formation occurs in the most overdense regions, which therefore reach a high metallicity (of order a tenth of the solar value) by z ~ 3, when the IGM metallicity is lower by 1 - 2 orders of magnitude. At later times, the formation of high-temperature clusters in the highest-density regions suppresses star formation there, while lower-density regions continue to increase their metallicity. Note, however, that the spatial resolution of the hydrodynamic code of Cen & Ostriker is a few hundred kpc, and anything occurring on smaller scales is inserted directly via simple parametrized models. Scannapieco & Broadhurst (2000) [317] implemented expanding outflows within a numerical scheme which, while not a full gravitational simulation, did include spatial correlations among halos. They showed that winds from low-mass galaxies may also strip gas from nearby galaxies (see also Scannapieco, Ferrara, & Broadhurst 2000 [318]), thus suppressing star formation in a local neighborhood and substantially reducing the overall abundance of galaxies in halos below a mass of ~ 10¹⁰ M. Although quasars do not produce metals, they may also affect galaxy formation in their vicinity via energetic outflows [116, 15, 339, 263].

Gnedin & Ostriker (1997) [148] and Gnedin (1998) [149] identified another mixing mechanism which, they argued, may be dominant at high redshift (z > 4). In a collision between two protogalaxies, the gas components collide in a shock and the resulting pressure force can eject a few percent of the gas out of the merger remnant. This is the merger mechanism, which is based on gravity and hydrodynamics rather than direct stellar feedback. Even if supernovae inject most of their metals in a local region, larger-scale mixing can occur via mergers. Note, however, that Gnedin's (1998) [149] simulation assumed a comoving star formation rate at z > 5 of ~ 1 M per year per comoving Mpc³, which is 5 - 10 times larger than the observed rate at redshift 3 - 4. Aguirre et al. [9] used outflows implemented in simulations to conclude that winds of ~ 300 km/s at z < 6 can produce the mean metallicity observed at z ~ 3 in the Ly forest. In a separate paper Aguirre et al. [10] explored another process, where metals in the form of dust grains are driven to large distances by radiation pressure, thus producing large-scale mixing without displacing or heating large volumes of IGM gas. The success of this mechanism depends on detailed microphysics such as dust grain destruction and the effect of magnetic fields. The scenario, though, may be directly testable because it leads to significant ejection only of elements which solidify as grains.

Feedback from galactic outflows encompasses a large variety of processes and influences. The large range of scales involved, from stars or quasars embedded in the interstellar medium up to the enriched IGM on cosmological scales, make possible a multitude of different, complementary approaches, promising to keep galactic feedback an active field of research.