3. SCATTERING OF LIGHT BY DUST: DEFINITIONS

As discussed in Section 2, when light impinges on a grain it is either scattered or absorbed. Let I_o() be the intensity of the incident light at wavelength , the intensity of light scattered into a direction defined by and (see Fig. 2) is

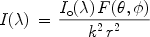(1)

where 0° 180° is the scattering angle (the angle from the incident direction), 0° 360° is the azimuthal angle which uniquely determines the scattering plane defined by the incident direction and the scattering direction (see Fig. 2), ² F(, ) is the (dimensionless) angular scattering function, r >> / 2 is the distance from the scatterer, and k = 2 / is the wave number in vacuum. The scattering cross section C_sca, defined as the area on which the incident wave falls with the same amount of energy as that scattered in all directions by the dust, may be obtained by integrating the angular scattering distribution F(, ) / k² over all solid angles

(2)

where F(, ) / k² (with a dimension of area), ³ after normalized by C_sca, is known as the phase function or scattering diagram

(3)

The asymmetry parameter (or asymmetry factor) g is defined as the average cosine of the scattering angle

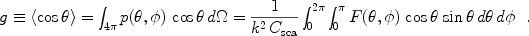(4)

The asymmetry parameter g, specifying the degree of scattering in the forward direction ( = 0°), varies from -1 (i.e. all radiation is backward scattered like a "mirror") to 1 (for pure forward scattering). If a grain scatters more light toward the forward direction, g > 0; g < 0 if the scattering is directed more toward the back direction; g = 0 if it scatters light isotropically (e.g. small grains in the Rayleigh regime) or if the scattering is symmetric with respect to = 90° (i.e. the scattered radiation is azimuthal independent and symmetric with respect to the plane perpendicular to the incident radiation).

Figure 2. Schematic scattering geometry of a dust grain in an incident radiation field of intensity Io which scatters radiation of intensity I(, ) into a scattering angle ( = 0°: forward scattering; = 180°: backward scattering), an azimuthal angle , and a distance r from the dust. In a Cartesian coordinate system, the incident direction defines the +z axis. The scattering direction and the incident direction define the scattering plane. In the far-field region (i.e. kr >> 1), I = Io F(, ) / k2r2, where k = 2 / is the wave number in vacuum.

In radiative transfer modeling of dusty regions, astronomers often use the empirical Henyey-Greenstein phase function to represent the anisotropic scattering properties of dust [26]

(5)

Draine (2003) proposed a more general analytic form for the phase function

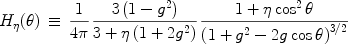(6)

where is an adjustable parameter. For = 0 Eq. 6 reduces to the Henyey-Greenstein phase function. For g = 0 and = 1 Eq. 6 reduces to the phase function for Rayleigh scattering [12].

As discussed in Section 2, both scattering and absorption (the sum of which is called extinction) remove energy from the incident beam. The extinction cross section, defined as

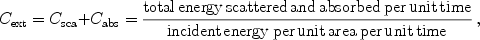(7)

is determined from the optical theorem which relates C_ext to the real part of the complex scattering amplitude S(, ) ⁴ in the forward direction alone [28]

(8)

The absorption cross section C_abs is the area on which the incident wave falls with the same amount of energy as that absorbed inside the dust; C_ext, having a dimension of area, is the "effective" blocking area to the incident radiation (for grains much larger than the wavelength of the incident radiation, C_ext is about twice the geometrical blocking area). For a grain (of size a and complex index of refraction m) in the Rayleigh limit (i.e. 2 a / << 1, 2 a |m| / << 1), the absorption cross section C_abs is much larger than the scattering cross section C_sca and therefore C_ext C_abs. Non-absorbing dust has C_ext = C_sca.

The albedo of a grain is defined as C_sca / C_ext. For grains in the Rayleigh limit, 0 since C_sca << C_abs. For Non-absorbing dust, = 1.

In addition to energy, light carries momentum of which the direction is that of propagation and the amount is h / c (where h is the Planck constant, c is the speed of light, and is the frequency of the light). Therefore, upon illuminated by an incident beam of light, dust will acquire momentum and a force called radiation pressure will be exerted on it in the direction of propagation of the incident light. The radiation pressure force is proportional to the net loss of the forward component of the momentum of the incident beam. While the momentum of the absorbed light (which is in the forward direction) will all be transfered to the dust, the forward component of the momentum of the scattered light will not be removed from the incident beam. Therefore, the radiation pressure force exerted on the dust is

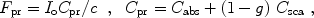(9)

where C_pr is the radiation pressure cross section, and I_o is the intensity (irradiance) of the incident light.

In literature, one often encounters Q_ext, Q_sca, Q_abs, and Q_pr - the extinction, scattering, absorption and radiation pressure efficiencies. They are defined as the extinction, scattering, absorption, and radiation pressure cross sections divided by the geometrical cross section of the dust C_geo,

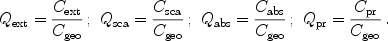(10)

For spherical grains of radii a, C_geo = a². For non-spherical grains, there is no uniformity in choosing C_geo. A reasonable choice is the geometrical cross section of an "equal volume sphere" C_geo (3V / 4)^2/3 1.21 V^2/3 where V is the volume of the non-spherical dust.

² When the scattering is along the incident direction ( = 0°, i.e. "forward scattering") or the scattering is on the opposite direction of the incident direction ( = 180°, i.e. "backward scattering"), any plane containing the z axis is a suitable scattering plane. Back.

³ Also called the "differential scattering cross section" dC_sca / d F(, ) / k², it specifies the angular distribution of the scattered light [i.e. the amount of light (for unit incident irradiance) scattered into a unit solid angle about a given direction]. Back.

⁴ The angular scattering function F(, ) is just the absolute square of the complex scattering amplitude S(, ): F(, ) = |S(, )|². Back.